8.3 Variación de pequeña escala \(\eta(s)\)
Recordemos que dividimos el proceso espacial en: \(Y(s) = \mu(s)+\eta(s)\) donde \(\mu(s)\) era la tendencia espacial (función determinística de covariables) y \(\eta(s)\) es un proceso espacial en \(\mathcal{D} \subset \mathbb{R}^r\).
Suponemos que \(\eta(s)\) es un proceso intrínisicamente estacionario con media cero, esto es:
\(E(\eta(s)) = 0\) para toda \(s\) en \(\mathcal{D}\)
- \(\frac{1}{2}Var(\eta(s) - \eta(s'))=\gamma(s-s')\)
Un proceso intríniscamente estacionario es un proceso que satisface las dos condiciones enumeradas, con media constante (pero no necesariamente cero). Notemos que podemos escribir la segunda condición como \[\frac{1}{2}Var(\eta(s) - \eta(s+h))=\gamma(h)\] y vemos que el lado derecho de la igualdad depende únicamnte de \(h\) (donde \(h \in \mathbb{R}^r\)) y no de la elección particular de \(s\).
La función \(2\gamma(h) = Var(\eta(s) - \eta(s+h))\) donde \(h \in \mathbb{R}^r\) se conoce como variograma, mientras que a \(\gamma(h)\) se le denota semivariograma.
¿Cómo se relaciona el variograma con la función de covarianzas \(C(h)\) (también conocida como covariograma)?
\[ \begin{align} \nonumber 2\gamma(h) &= Var(\eta(s+h) - \eta(s))\\ \nonumber &=Var(\eta(s+h)) + Var(\eta(s)) - 2Cov(\eta(s+h), \eta(s))\\ \nonumber &= C(0) + C(0) -2Cov(\eta(s+h), \eta(s))\\ \nonumber &=2[C(0) - C(h)] \end{align} \]
Vemos entonces que \(\gamma(h) = C(0)-C(h)\) y por tanto si conocemos \(C\) podemos recuperar \(\gamma\); sin embargo, para ir de \(\gamma\) a \(C\) nesesitamos un supuesto adicional: si el proceso espacial cumple \(C(h) \rightarrow 0\) cuando \(\|h\| \to \infty\) (ergódico), tomando limites en la igualdad \(\gamma(h) = C(0)-C(h)\) vemos que \[\lim_{\|h\| \to \infty} \gamma(h) = C(0)\] y podemos recuperar \(C\) de \(\gamma\) utilizando la variable auxiliar \(u\) de la siguiente manera, \[C(h) = C(0) - \gamma(h) = \lim_{\|u\| \to \infty} \gamma(u) - \gamma(h)\] El límite del lado derecho no existe siempre (si existe se decieque el proceso es estacionario de segundo orden), estudiaremos casos en los que existe.
Veamos que el supuesto de ergodicidad es sensible (intuitivamente) pues nos dice que la covarianza entre dos puntos desaparece conforme los puntos se separan en el espacio.
Utilizaremos estos conceptos en la estimación de \(\eta(s)\), primero aproximamos los residuales como \[\hat{\eta}(s_i) = Y(s_i) - \hat{\mu}(s_i)\] para \(i = 1,...,n\) donde \(\hat{\mu}(s)\) es la tendencia estimada.
8.3.1 Semivariograma empírico
Como parte del análisis exploratorio de datos es útil graficar el semivariograma empírico \(\hat{\gamma}(h)\) definido como (si las observaciones están en una cuadrilla regular):
\[\hat{\gamma}(h) = \frac{1}{2N(h)}\sum_{i,j:s_i-s_j = h}(\hat{\eta}(s_i)- \hat{\eta}(s_j))^2\]
donde \(N(h)\) es el número de pares \((s_i, s_j)\) tales que \(s_i-s_j = h\).
Si las observaciones no están en una cuadrilla regular definimos regiones de tolerancia \(T(h)\) (vecindades alrededor de h) para cada \(h\):
\[\hat{\gamma}(h) = \frac{1}{2\#T(h)}\sum_{i,j:s_i-s_j \in T(h)}(\hat{\eta}(s_i)- \hat{\eta}(s_j))^2\]
En la práctica para construir el semivariograma empírico seguimos los siguientes pasos:
Particionamos el espacio de todas las diferencias \(\mathcal{H}=\{s-s': s, s' \in \mathcal{D} \}\) en clases (bins) \(B_m\).
Calculamos las diferencias \(s_i-s_j\) para toda \(i\neq j\) y las asignamos a una clase \(B_m\).
Determinamos \(h_m\) el vector diferencia representativo de la clase \(B_m\), \(h_m\) puede ser el promedio de todas las diferencias \(s_i-s_j\) que caen en la clase \(m\).
Determinamos el número de pares ordenados \((s_i,s_j)\) tales que \(s_i-s_j \in B_m\) y calculamos \(N(h_m)=\#B_m\).
Para \(h_m\) claculamos:
\[\hat{\gamma}(h_m) = \frac{1}{2N(h_m)}\sum_{i,j:s_i-s_j = h}(\hat{\eta}(s_i)- \hat{\eta}(s_j))^2\]
Grafiquemos el semivariograma empírico para el ejmplo de ph.
library(gstat)
#> Registered S3 method overwritten by 'xts':
#> method from
#> as.zoo.xts zoo
#>
#> Attaching package: 'gstat'
#> The following object is masked from 'package:spatstat':
#>
#> idw
mod.1 <- lm(pH_water ~ x + y, data = soil)
soil$eta.hat <- soil$pH_water - mod.1$fitted.values
# formato para gstat
water.data <- data.frame(x = soil$x, y = soil$y, eta.hat = soil$eta.hat)
coordinates(water.data) = ~ x + y
emp.variog <- variogram(eta.hat ~ 1, water.data)
emp.variog
#> np dist gamma dir.hor dir.ver id
#> 1 465 5.000000 0.01205687 0 0 var1
#> 2 432 7.071068 0.01829269 0 0 var1
#> 3 1228 10.767029 0.02318624 0 0 var1
#> 4 368 14.142136 0.03156926 0 0 var1
#> 5 1127 15.527006 0.02877962 0 0 var1
#> 6 674 18.027756 0.03648034 0 0 var1
#> 7 1946 21.145090 0.03327388 0 0 var1
#> 8 1483 25.200309 0.03282693 0 0 var1
#> 9 802 27.352668 0.03609339 0 0 var1
#> 10 1324 29.847701 0.03265740 0 0 var1
#> 11 1380 32.365272 0.03640711 0 0 var1
#> 12 1745 35.717469 0.03240342 0 0 var1
#> 13 734 38.542536 0.03415193 0 0 var1
#> 14 1480 40.708458 0.03253772 0 0 var1
# plot(emp.variog)
# graficar el semivariograma empírico (notemos que estamos asumiendo
# un proceso isotrópico)
# plot(emp.variog, col = "black", type = "p",pch=20)
ggplot(emp.variog, aes(x = dist, y = gamma)) +
geom_point() + ylim(0, 0.038) +
labs(title = expression("Semivariograma empírico"),
x = "distancia", y = "semivarianza")
Una definición más:
Un proceso intrínsicamente estacionario es isotrópico si su semivariograma \(\gamma(h)\) depende del vector de separación \(h\) únicamente a través de su norma \(\|h\|\).
Entonces, para un proceso istrópico \(\gamma(h)\) es una función univariada que se puede escribir como \(\gamma(\|h\|)\). Los procesos istrópicos son populares debido a su simplicidad y a que existen varias funciones paramétricas que se pueden utilizar para definir el semivariograma del proceso.
Nos podemos preguntar si en el ejemplo es razonable suponer que el proceso es isotrópico.
water.data <- data.frame(x = soil$x, y = soil$y, eta.hat = soil$eta.hat)
coordinates(water.data) = ~ x + y
dir.variog <- variogram(eta.hat ~ 1, water.data, alpha = c(0,45,90,135))
# plot(dir.variog)
# ggplot
dir.variog$direction <- factor(dir.variog$dir.hor, levels = c(0, 45, 90, 135),
labels = c("E-O", "NE-SO", "N-S", "NO-SE"))
ggplot(dir.variog, aes(x = dist, y = gamma, colour = direction)) +
geom_point(size = 1.8) +
labs(title = expression("Semivariograma direccional"),
x = "distancia", y = "semivariance", colour = "dirección") + geom_line()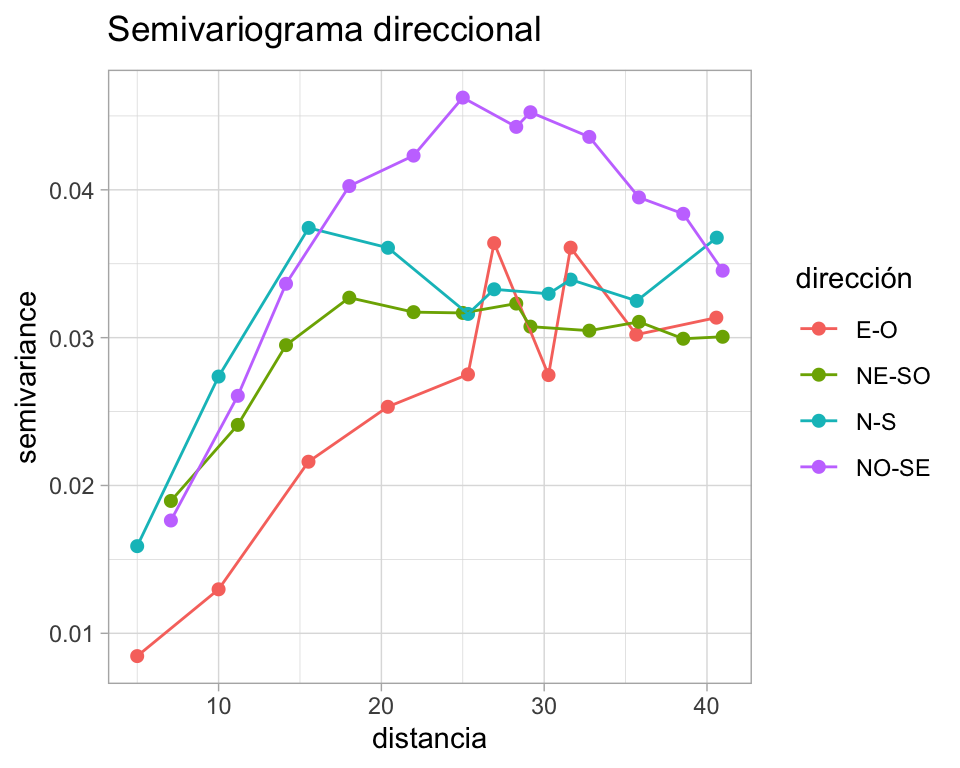
# cuando invesigamos anisotropías podemos tener celdas con pocos datos
dir.variog
#> np dist gamma dir.hor dir.ver id direction
#> 1 240 5.000000 0.008458055 0 0 var1 E-O
#> 2 230 10.000000 0.012975878 0 0 var1 E-O
#> 3 616 15.521607 0.021606792 0 0 var1 E-O
#> 4 588 20.395697 0.025322388 0 0 var1 E-O
#> 5 560 25.318277 0.027516438 0 0 var1 E-O
#> 6 320 26.925824 0.036397520 0 0 var1 E-O
#> 7 532 30.266022 0.027468345 0 0 var1 E-O
#> 8 304 31.622777 0.036088812 0 0 var1 E-O
#> 9 792 35.654657 0.030202126 0 0 var1 E-O
#> 10 748 40.575002 0.031353430 0 0 var1 E-O
#> 11 216 7.071068 0.018954083 45 0 var1 NE-SO
#> 12 399 11.180340 0.024098014 45 0 var1 NE-SO
#> 13 184 14.142136 0.029493385 45 0 var1 NE-SO
#> 14 337 18.027756 0.032705246 45 0 var1 NE-SO
#> 15 460 21.976525 0.031726106 45 0 var1 NE-SO
#> 16 279 25.000000 0.031671985 45 0 var1 NE-SO
#> 17 126 28.284271 0.032306561 45 0 var1 NE-SO
#> 18 250 29.154759 0.030745742 45 0 var1 NE-SO
#> 19 446 32.771480 0.030473847 45 0 var1 NE-SO
#> 20 298 35.820555 0.031069845 45 0 var1 NE-SO
#> 21 367 38.542536 0.029926745 45 0 var1 NE-SO
#> 22 247 40.962094 0.030059470 45 0 var1 NE-SO
#> 23 225 5.000000 0.015895598 90 0 var1 N-S
#> 24 200 10.000000 0.027369239 90 0 var1 N-S
#> 25 511 15.533516 0.037426326 90 0 var1 N-S
#> 26 438 20.404731 0.036080069 90 0 var1 N-S
#> 27 365 25.325544 0.031604801 90 0 var1 N-S
#> 28 230 26.925824 0.033271633 90 0 var1 N-S
#> 29 292 30.272096 0.032967634 90 0 var1 N-S
#> 30 184 31.622777 0.033928552 90 0 var1 N-S
#> 31 357 35.684719 0.032487913 90 0 var1 N-S
#> 32 238 40.601432 0.036763848 90 0 var1 N-S
#> 33 216 7.071068 0.017631307 135 0 var1 NO-SE
#> 34 399 11.180340 0.026063391 135 0 var1 NO-SE
#> 35 184 14.142136 0.033645130 135 0 var1 NO-SE
#> 36 337 18.027756 0.040255433 135 0 var1 NO-SE
#> 37 460 21.976525 0.042313738 135 0 var1 NO-SE
#> 38 279 25.000000 0.046239751 135 0 var1 NO-SE
#> 39 126 28.284271 0.044258667 135 0 var1 NO-SE
#> 40 250 29.154759 0.045249016 135 0 var1 NO-SE
#> 41 446 32.771480 0.043579863 135 0 var1 NO-SE
#> 42 298 35.820555 0.039486207 135 0 var1 NO-SE
#> 43 367 38.542536 0.038377105 135 0 var1 NO-SE
#> 44 247 40.962094 0.034530260 135 0 var1 NO-SE8.3.1.1 Observaciones
- ¿Cómo elegimos el tamaño de los bins \(B_m\)? ¿Cuántos bins?
Más bins puede ser más informativo; sin embargo, bins con pocas observaciones pueden ser muy ruidosos. Una regla de dedo es definirlos para que contengan al menos 30 observaciones.
set.seed(1362)
soil.2 <- soil[sample(1:nrow(soil), size = 90), ]
water.data <- data.frame(x = soil.2$x, y = soil.2$y, eta.hat = soil.2$eta.hat)
coordinates(water.data) = ~ x + y
emp.variog.1 <- variogram(eta.hat ~ 1, water.data)
emp.variog.1$variogram <- "default"
emp.variog.2 <- variogram(eta.hat ~ 1, water.data, width = 0.1)
emp.variog.2$variogram <- "pocas obs."
emp.variog.3 <- variogram(eta.hat ~ 1, water.data, width = 9)
emp.variog.3$variogram <- "pocos bins"
emp.variogs <- rbind(emp.variog.1, emp.variog.2, emp.variog.3)
ggplot(emp.variogs, aes(x = dist, y = gamma, color = variogram, group = variogram)) +
geom_point() +
geom_line() +
ylim(0, 0.06) +
labs(title = expression("Semivariograma empírico"),
x = "distancia", y = "semivarianza")
- La variabilidad en el valor de \(\hat{\gamma}(h)\) aumenta conforme \(\|h\|\) aumenta, por lo que \(\hat{\gamma}(h)\) es poco confiable para valores grandes de \(\|h\|\). Es aconsejable establecer una cota superior a la magnitud de \(\|h\|\), una regla de dedo es usar 1/2 de la máxima distancia.
Corrobora el punto 2 en el ejemplo de
ph.
8.3.2 Semivariogramas paramétricos
Modelamos el semivariograma empírico utilizando semivariogramas paramétricos, hay varias razones por las cuales esto es conveniente:
El semivariograma empírico no esta disponible en distancias que no aparecen en los datos.
El semivariograma empírico puede ser muy ruidoso por lo que una verisón suavizada puede ser más confiable.
El semivariograma empírico puede no cumplir los supuestos necesarios para estimar el proceso.
Hay varias características que debe cumplir el semivariogreama paramétrico, por ejemplo, es una función no-decreciente de la distancia. Es común que el semivariograma empírico se aplane a partir de un cierto punto, indicando que la dependencia espacial disminuye con la distancia, si es el caso el semivariograma paramétrico debe reflejar este escenario. Veamos algunos modelos de semivariogramas paramétricos:
8.3.2.1 Esférico
\[\gamma(h;\theta) = \left\{ \begin{array}{lr} 0 & : \|h\| = 0 \\ \tau^2 +\sigma^2\big(\frac{3\|h\|}{2\phi}-\frac{\|h\|^3}{2\phi^3}\big) & : 0 \le \|h\| \le \phi\\ \tau^2+\sigma^2 & : \|h\| > 0 \end{array} \right. \] donde \(\sigma^2, \phi>0\). Esta modelo del semivariograma tiene asociada la siguiente función de covarianza:
\[C(h;\theta) = \left\{ \begin{array}{lr} \tau^2 + \sigma^2 & : \|h\| = 0 \\ \sigma^2\left(1-\big(\frac{3\|h\|}{2\phi}-\frac{\|h\|^3}{2\phi^3}\big)\right) & : 0 < \|h\| \le \phi\\ 0 & : \|h\| > \phi \end{array} \right. \]
sph.variog <- function(sigma2, phi, tau2, dist){
n <- length(dist)
sph.variog.vec <- rep(0,n)
for(i in 1:n){
if(dist[i] < phi){
sph.variog.vec[i] <- tau2 + (sigma2 * (((3 * dist[i]) / (2 * phi)) -
((dist[i] ^ 3)/(2 * (phi ^ 3)))))
}
if(dist[i] >= phi){
sph.variog.vec[i] <- tau2 + sigma2
}
}
return(sph.variog.vec)
}
dat <- data.frame(x = seq(0, 10, 1), y = seq(0, 1, 0.1))
ggplot(dat, aes(x = x, y = y)) +
labs(title = expression("Semivariograma esférico"),
x = "distancia", y = "semivarianza") +
stat_function(fun = sph.variog, args = list(sigma2 = 1, phi = 1, tau2 = 0),
colour = "green3") +
stat_function(fun = sph.variog, args = list(sigma2 = 1, phi = 8, tau2 = 0),
colour = "orange") +
stat_function(fun = sph.variog, args = list(sigma2 = 0.5, phi = 1, tau2 = 0),
colour = "steelblue") +
stat_function(fun = sph.variog, args = list(sigma2 = 1, phi = 1, tau2 = 0.2),
colour = "darkgray")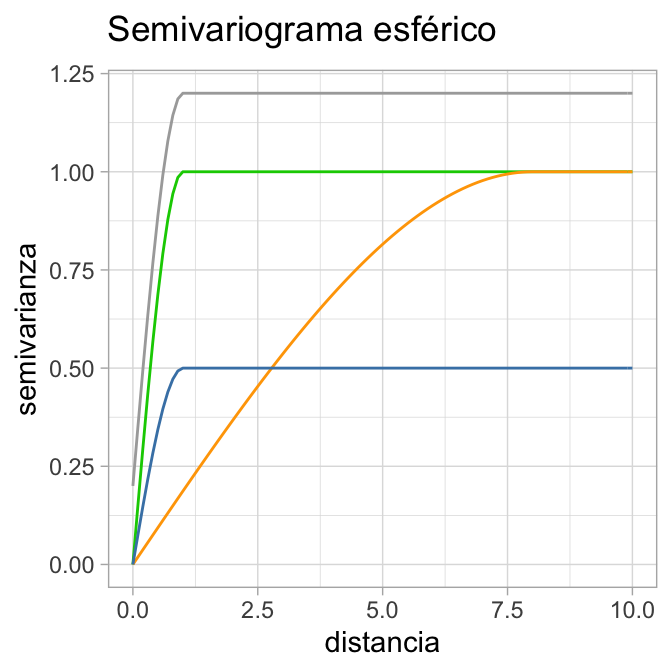 
Un semivariograma paramétrico tiene las siguientes características:
- Por definición \(\gamma(0) = 0\). Sin embargo, en ocasiones vemos que el valor en cero del semivariograma empírico es \(\tau^2\neq 0\). En geostadística \[\tau^2=\gamma(0^+)=\lim_{\|h\|\to 0^+} \gamma(t)\] se conoce como el efecto nugget o pepita. El efecto nugget equivale a descomponer \(\eta(s)\) como \[\eta(s)=\eta'(s)+\epsilon\] donde \(\epsilon\) es ruido blanco. La siguiente figura muestra el efecto del nugget en un proceso simulado, en el lado izquierdo \(\tau^2 = 0\) y en el del lado derecho \(\tau^2 = 0.5\).
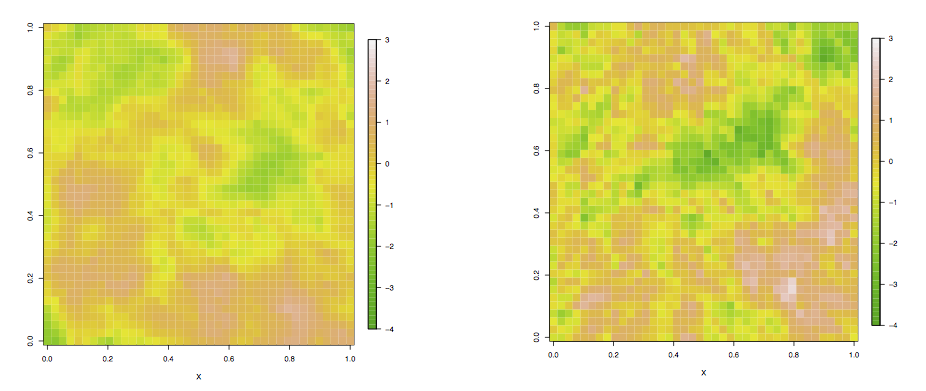
\(lim_{\|h\|\to \infty} \gamma(\|h\|) = \tau^2 + \sigma^2\), este valor (asintótico normalmente) del semivariograma se conoce como el silo, el silo menos el nugget se conoce como silo parcial y es simplemente \(\sigma^2\). El silo no siempre exite.
El rango es el menor valor de \(\|h\|\) en el que el semivariograma alcanza el silo (\(\phi\)).
En el caso del semivariograma gris
del ejemplo de arriba, ¿Cuál es el nugget, silo parcial y el rango?
- 0.2, 1.2, 1
- 0.2, 1, 1
- 0, 1, 1
- 0, 1.2, 1
- Ninguna de las anteriores
8.3.2.2 Gaussiano
\[\gamma(h;\theta) = \left\{ \begin{array}{lr} 0 & : \|h\| = 0 \\ \tau^2 +\sigma^2\big(1-exp\big(-\frac{\|h\|^2}{\phi^2}\big)\big) & : \|h\| > 0 \end{array} \right. \] donde \(\sigma^2, \phi>0\). Con función de covarianza:
\[C(h;\theta) = \left\{ \begin{array}{lr} \tau^2 + \sigma^2 & : \|h\| = 0 \\ \sigma^2\left(1- \big(1-exp\big(-\frac{\|h\|^2}{\phi^2}\big)\big)\right) & : \|h\| > 0 \end{array} \right. \]
# existen funciones en los paquetes pero escribirlas puede ser ilustrativo
gau.variog <- function(sigma2,phi,tau2,dist){
n <- length(dist)
gau.variog.vec <- rep(0,n)
for(i in 1:n){
gau.variog.vec[i] <- tau2 + sigma2 * (1-exp(-dist[i]^2/phi^2))
}
gau.variog.vec[0] <- 0
return(gau.variog.vec)
}
dat <- data.frame(x = seq(0, 10, 1), y = seq(0, 1, 0.1))
ggplot(dat, aes(x = x, y = y)) +
labs(title = expression("Semivariograma gaussiano"),
x = "distancia", y = "semivarianza") +
stat_function(fun = gau.variog, args = list(sigma2 = 1, phi = 1, tau2 = 0),
colour = "green3") +
stat_function(fun = gau.variog, args = list(sigma2 = 1, phi = 8, tau2 = 0),
colour = "orange") +
stat_function(fun = gau.variog, args = list(sigma2 = 0.5, phi = 1, tau2 = 0),
colour = "steelblue") +
stat_function(fun = gau.variog, args = list(sigma2 = 1, phi = 1, tau2 = 0.2),
colour = "darkgray") + xlim(0, 20)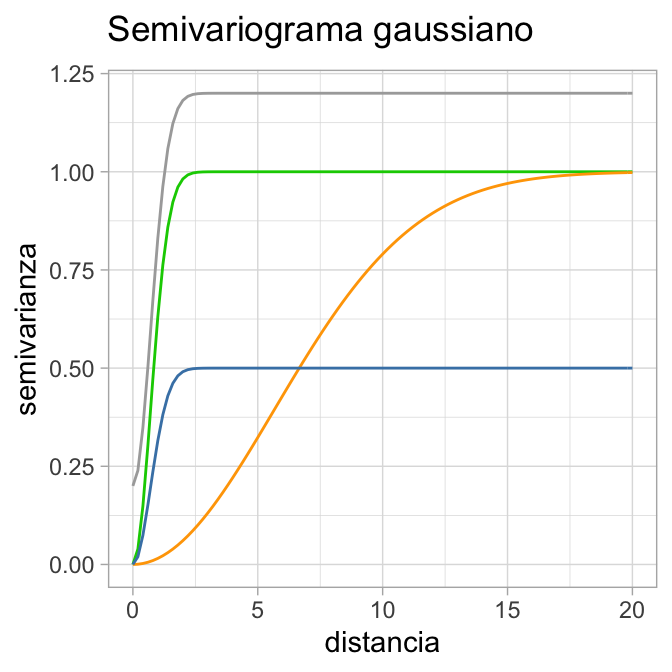
8.3.2.3 Matérn
\[\gamma(h;\theta) = \left\{ \begin{array}{lr} 0 & : \|h\| = 0 \\ \tau^2 +\sigma^2 \left(1-\frac{\big(2\sqrt{\nu} \frac{\|h\|}{\phi}\big)^{\nu} \mathcal{K}_\nu\big(2\sqrt{\nu}\frac{\|h\|}{\phi}\big)} {2^{\nu-1}\Gamma(\nu)}\right) & : \|h\| > 0 \end{array} \right. \] donde \(\sigma^2, \phi>0\).
Notemos que esta función tiene el parámetro adicional \(\nu\), este controla el suavizamiento del proceso espacial. El semivariograma exponencial es un caso especial del Matern con \(\nu = 1/2\), el Gaussiano se puede derivar del Matern haciendo \(\nu \to \infty\).
library(geoR)
mat.variog <- function(sigma2, phi, tau2, nu = 1, dist){
#phi <- 2*phi
n <- length(dist)
mat.variog.vec <- rep(0,n)
for(i in 1:n){ # in fun matern u = 2*sqrt(nu)*dist
mat.variog.vec[i] <- tau2 + sigma2 * (1 - geoR::matern(2*sqrt(nu)*dist[i],
phi, nu))
}
return(mat.variog.vec)
}
dat <- data.frame(x = seq(0, 10, 1), y = seq(0, 1, 0.1))
mat_1 <- ggplot(dat, aes(x = x, y = y)) +
labs(x = "distancia", y = "semivarianza") +
stat_function(fun = mat.variog, args = list(sigma2 = 1, phi = 1, tau2 = 0,
nu = 1/4), colour = "green3") +
stat_function(fun = mat.variog, args = list(sigma2 = 1, phi = 8, tau2 = 0,
nu = 1/4), colour = "orange") +
stat_function(fun = mat.variog, args = list(sigma2 = 0.5, phi = 1, tau2 = 0,
nu = 1/4), colour = "steelblue") +
stat_function(fun = mat.variog, args = list(sigma2 = 1, phi = 1, tau2 = 0.2,
nu = 1/4), colour = "darkgray")
mat_2 <- ggplot(dat, aes(x = x, y = y)) +
labs(x = "distancia", y = "semivarianza") +
stat_function(fun = mat.variog, args = list(sigma2 = 1, phi = 1, tau2 = 0,
nu = 10), colour = "green3") +
stat_function(fun = mat.variog, args = list(sigma2 = 1, phi = 8, tau2 = 0,
nu = 10), colour = "orange") +
stat_function(fun = mat.variog, args = list(sigma2 = 0.5, phi = 1, tau2 = 0,
nu = 10), colour = "steelblue") +
stat_function(fun = mat.variog, args = list(sigma2 = 1, phi = 1, tau2 = 0.2,
nu = 10), colour = "darkgray") + xlim(0, 20)
grid.arrange(mat_1, mat_2, ncol = 2)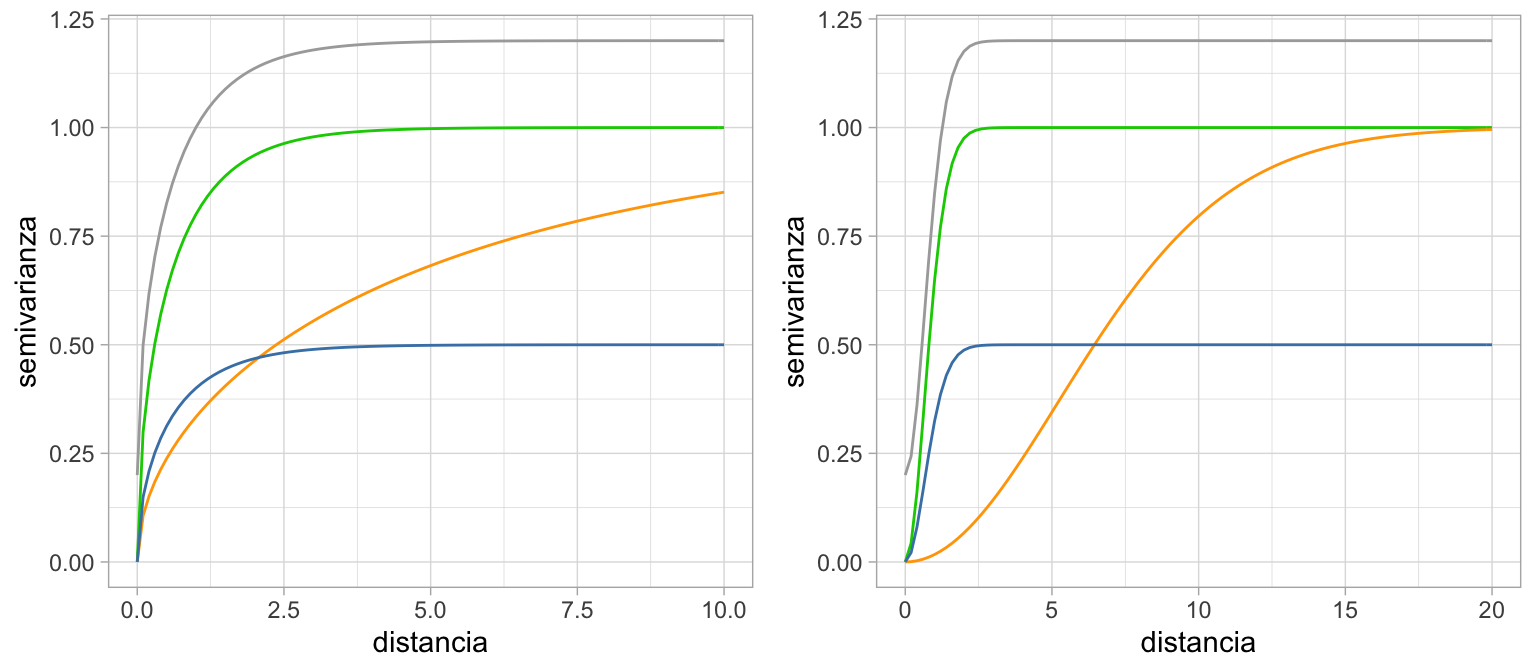
Vimos distintos modelos de variogramas paramétricos, ¿Cuál es la diferencia práctica entre ellos? Producen distintos tipos de dependencia espacial y distintos procesos espaciales.
grid.xy <- expand.grid(x = seq(0, 2, 0.02), y = seq(0, 2, 0.02))
# Esférico
esf_sin <- gstat(formula = z ~ 1, locations = ~ x + y, beta = 1, dummy = TRUE,
model = vgm(psill = 1, model = "Sph", range = 1), nmax = 20)
# make 4 simulaciones
set.seed(23)
esf <- predict(esf_sin, newdata = grid.xy, nsim = 4)
#> [using unconditional Gaussian simulation]
esf_df <- melt(esf, id.vars = c("x", "y"))
cuts <- seq(min(esf_df$value) - 1, max(esf_df$value) + 1, length = 10)
esf_df$data_cat <- cut(esf_df$value, breaks = cuts, include.lowest = TRUE)
esf_df$tipo <- "Sin nugget"
# Esférico con nugget
esf_con <- gstat(formula = z ~ 1, locations = ~ x + y, beta = 1, dummy = TRUE,
model = vgm(psill = 1, model = "Sph", range = 1, nugget = 0.2), nmax = 20)
# hacemos 4 simulaciones
set.seed(23)
esf <- predict(esf_con, newdata = grid.xy, nsim = 4)
#> [using unconditional Gaussian simulation]
esf_df_2 <- melt(esf, id.vars = c("x", "y"))
esf_df_2$data_cat <- cut(esf_df_2$value, breaks = cuts, include.lowest = TRUE)
esf_df_2$tipo <- "Con nugget"
esf_df_3 <- rbind(esf_df, esf_df_2)
ggplot(esf_df_3, aes(x = x, y = y, color = data_cat)) +
geom_point(size = 1.8) +
scale_colour_brewer(palette = "Blues", drop = FALSE) +
facet_grid(tipo ~ variable) +
labs(title = "Esférico")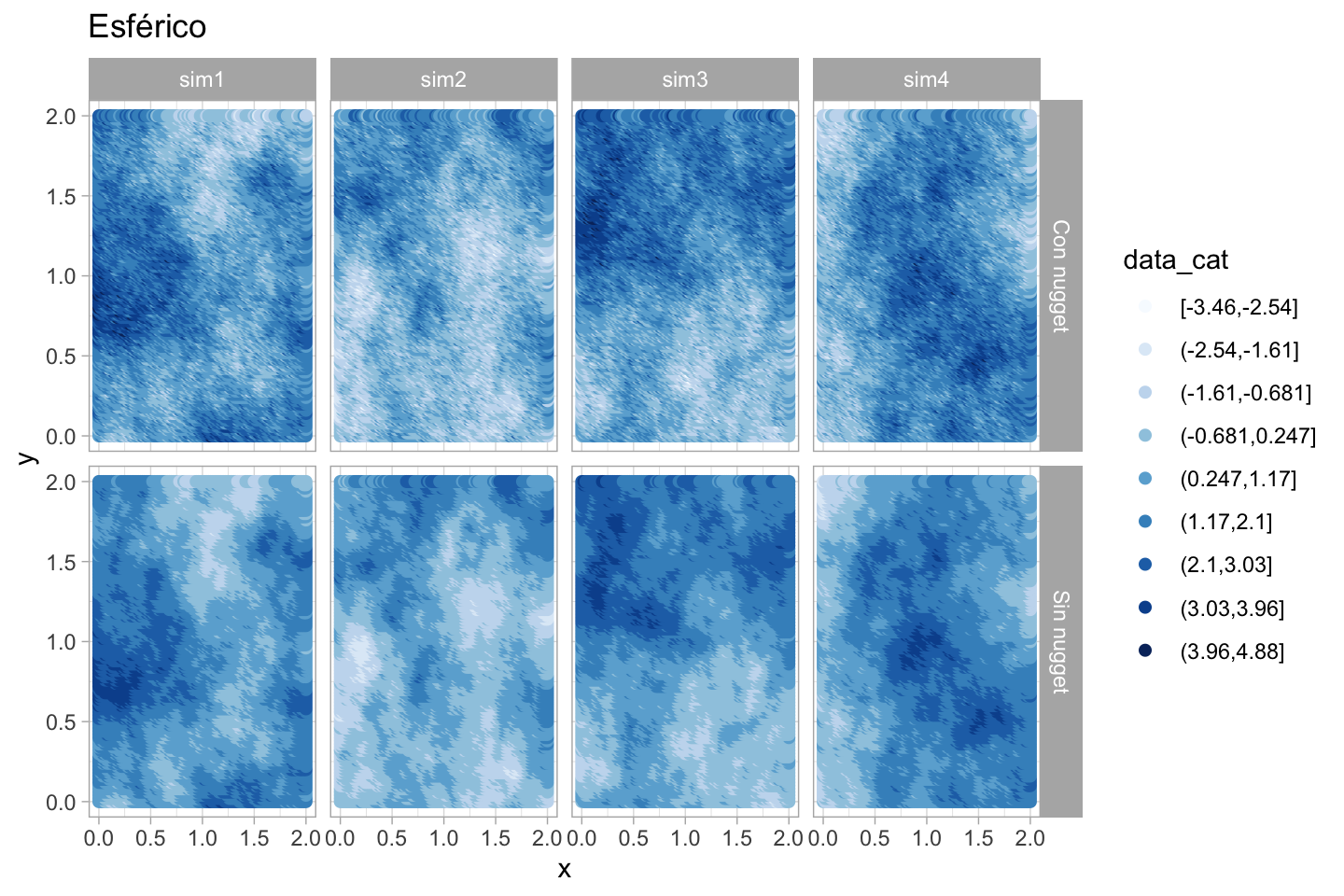
# Gaussiano
grid.xy <- expand.grid(x = seq(0, 2, 0.02), y = seq(0, 2, 0.02))
gau_sin <- gstat(formula = z ~ 1, locations = ~ x + y, beta = 1, dummy = TRUE,
model = vgm(psill = 1, model = "Gau", range = 1, nugget = 0.0001), nmax = 20)
# make 4 simulations
set.seed(23)
gau <- predict(gau_sin, newdata = grid.xy, nsim = 4)
#> [using unconditional Gaussian simulation]
gau_df <- melt(gau, id.vars = c("x", "y"))
cuts <- seq(min(gau_df$value)-0.5, max(gau_df$value)+0.5, length = 10)
gau_df$data_cat <- cut(gau_df$value, breaks = cuts, include.lowest = TRUE)
gau_df$tipo <- "Sin nugget"
# Gaussiano con nugget
gau_con <- gstat(formula = z ~ 1, locations = ~ x + y, beta = 1, dummy = TRUE,
model = vgm(psill = 1, model = "Gau", range = 1, nugget = 0.05), nmax = 20)
set.seed(23)
gau <- predict(gau_con, newdata = grid.xy, nsim = 4)
#> [using unconditional Gaussian simulation]
gau_df_2 <- melt(gau, id.vars = c("x", "y"))
gau_df_2$data_cat <- cut(gau_df_2$value, breaks = cuts, include.lowest = TRUE)
gau_df_2$tipo <- "Con nugget"
gau_df_3 <- rbind(gau_df, gau_df_2)
ggplot(gau_df_3, aes(x = x, y = y, color = data_cat)) +
geom_point(size = 1.8) +
scale_colour_brewer(palette = "Blues", drop = FALSE) +
facet_grid(tipo ~ variable) +
labs(title = "Gaussiano")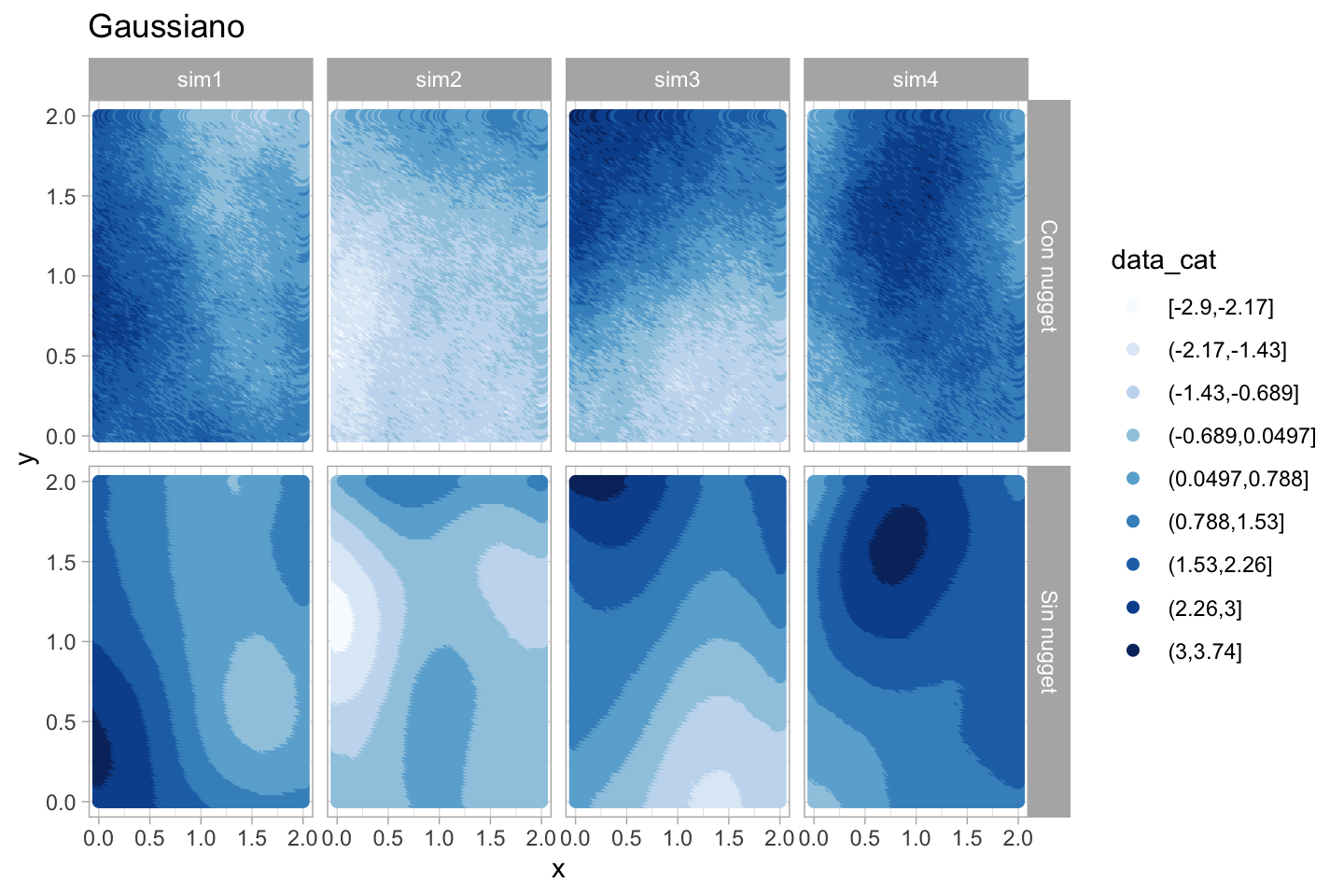
8.3.3 Estimación de \(\eta(s)\)
Veremos la estimación de \(\eta(s)\) utilizando técnicas de geosestadística clásica y de máxima verosimilitud.
8.3.3.1 Geoestadística clásica
Una vez que elegimos el modelo paramétrico que vamos a usar (esférico, gaussiano, etc.) etsimamos los valores de los parámetros usando mínimos cuadrados ponderados (donde se da un mayor peso a observaciones cercanas pues la varianza suele ser menor). \[WSS(\theta) = \sum_{m=1}^k \frac{N(h_m)}{(\gamma(h_m:\theta))^2}(\hat{\gamma}(h_m) -\gamma(h_m:\theta))^2\] El estimador de \(\theta\) se encuentra minimizando de manera iterativa la suma de cuadrados ponderada (\(WSS(\theta)\)).
Ajustemos los semivariogramas paramétricos a nuestros datos usando WLS.
#### Variograma esférico
sph.variog.w <- fit.variogram(emp.variog, vgm(psill= 0.02, model="Sph",
range = 20, nugget = 0.012),fit.method = 2)
sph.variog.w
#> model psill range
#> 1 Nug 0.0009100885 0.00000
#> 2 Sph 0.0327351959 20.94911
print(plot(emp.variog, sph.variog.w))
# Estimaciones
sigma2.sph <- sph.variog.w$psill[2]
phi.sph <- sph.variog.w$range[2]
tau2.sph <- sph.variog.w$psill[1]
dist.vec <- emp.variog$dist # vector de distancias
sph.variog.2 <- sph.variog(sigma2.sph,phi.sph,tau2.sph,dist.vec)
# Gaussiano
gau.variog.w <- fit.variogram(emp.variog, vgm(psill= 0.02, model="Gau",
range = 20, nugget = 0.012), fit.method = 2)
gau.variog.w
#> model psill range
#> 1 Nug 0.005615801 0.000000
#> 2 Gau 0.028258247 7.805675
print(plot(emp.variog, gau.variog.w))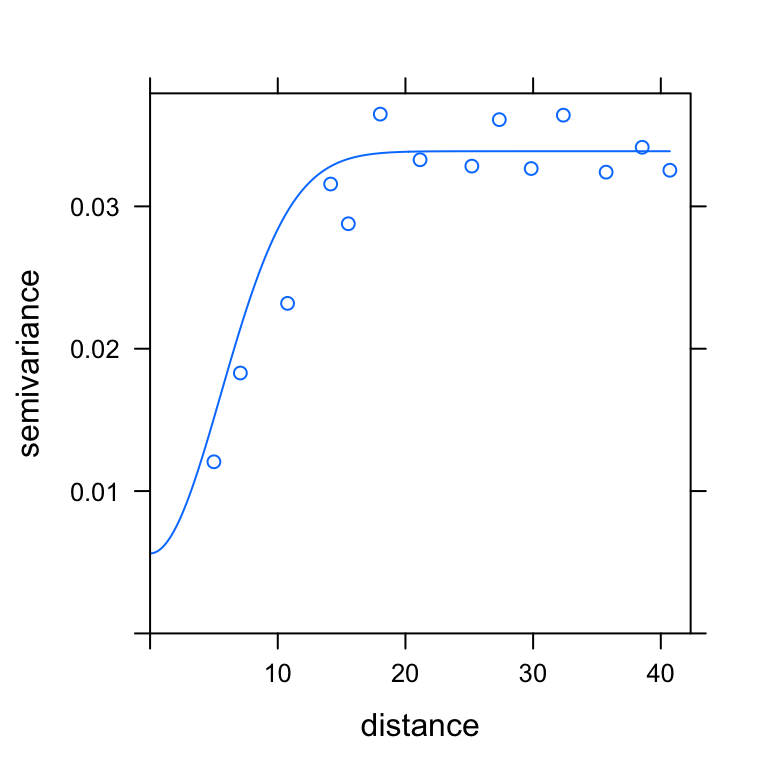
sigma2.gau <- gau.variog.w$psill[2]
phi.gau <- gau.variog.w$range[2]
tau2.gau <- gau.variog.w$psill[1]
gau.variog.2 <- gau.variog(sigma2.gau, phi.gau, tau2.gau, dist.vec)
# Matern
mat.variog.w <- fit.variogram(emp.variog, vgm(psill = 0.02, model = "Mat",
range = 20, nugget = 0.012, kappa = 1), fit.method = 2)
mat.variog.w
#> model psill range kappa
#> 1 Nug 0.00000000 0.000000 0
#> 2 Mat 0.03485972 5.626509 1
print(plot(emp.variog, mat.variog.w))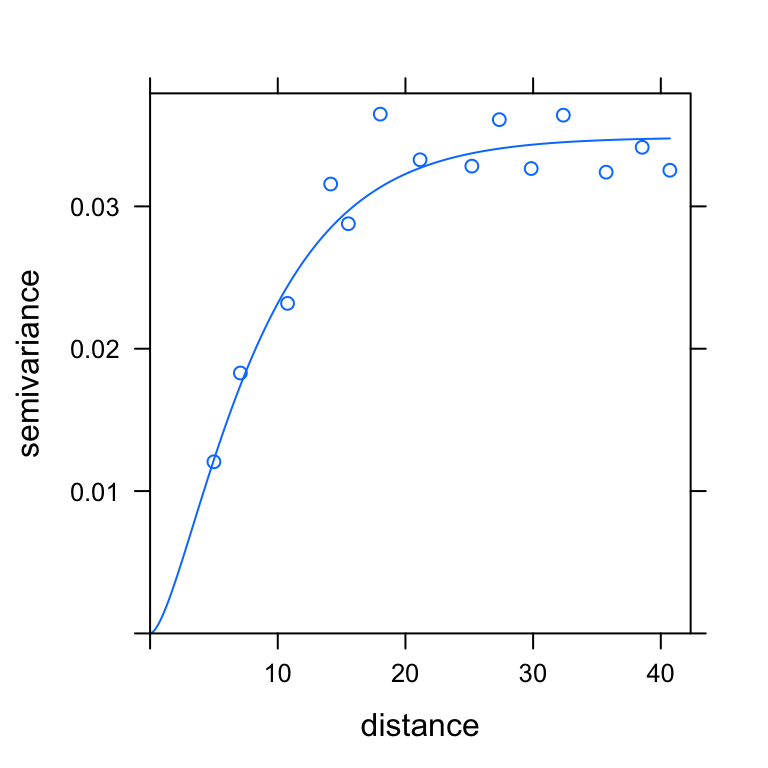
sigma2.mat <- mat.variog.w$psill[2]
phi.mat <- 2*mat.variog.w$range[2]
tau2.mat <- mat.variog.w$psill[1]
nu.mat <- mat.variog.w$kappa[2]
mat.variog.2 <- mat.variog(sigma2.mat,phi.mat,tau2.mat,nu.mat,dist.vec)
# Evaluación de los modelos
### Calculamos la suma de cuadrados ponderada (WSS)
weights.sph <- emp.variog$np/((sph.variog.2)^2)
squared.diff.sph <- (emp.variog$gamma - sph.variog.2)^2
wss.sph <- sum(weights.sph * squared.diff.sph)
wss.sph
#> [1] 40.44543
weights.gau <- emp.variog$np/((gau.variog.2)^2)
squared.diff.gau <- (emp.variog$gamma-gau.variog.2)^2
wss.gau <- sum(weights.gau * squared.diff.gau)
wss.gau
#> [1] 133.4418
weights.mat <- emp.variog$np/((mat.variog.2)^2)
squared.diff.mat <- (emp.variog$gamma-mat.variog.2)^2
wss.mat <- sum(weights.mat * squared.diff.mat)
wss.mat
#> [1] 53.1714
ggplot(emp.variog, aes(x = dist, y = gamma)) +
geom_point() +
labs(title = expression("Semi-variogramas"),
x = "distancia", y = "semivarianza") +
stat_function(fun = gau.variog, args = list(sigma2 = sigma2.gau, phi = phi.gau, tau2 = tau2.gau), colour = "green3") +
stat_function(fun = sph.variog, args = list(sigma2 = sigma2.sph, phi = phi.sph, tau2 = tau2.sph), colour = "orange") +
stat_function(fun = mat.variog, args = list(sigma2 = sigma2.mat, phi = phi.mat,
tau2 = tau2.mat, nu = nu.mat), colour = "steelblue") +
ylim(0, 0.038) + xlim(0, 45)
Una vez que tenemos la estimación de los parámetros del semivariograma debemos recalcular la tendencia, par esto usaremos Mínimos cuadrados generalizados (GLS): \[ Y = X\beta+ \epsilon\] donde \(\epsilon\sim N_n(0, \Sigma)\), si conocemos \(\Sigma\) el estimador de \(\beta\) es: \(\hat{\beta}_{GLS} = (X'\Sigma^{-1}X)^{-1}X'\Sigma^{-1}Y\).
De esta manera, el procedimiento de geostadística clásica es como sigue:
Obtenemos un estimador provisional de \(\beta\) usando OLS.
Calculamos los residuales usando \(\hat{\beta}_{OLS}\) y ajustamos un semivariograma paramétrico usando WLS.
Construimos la matriz de covarianzas utilizando la función de covarianzas \(C(h:\theta)\) al semivariograma paramétrico que elegimos \(\gamma(h:\theta)\), \(\hat{\Sigma}_{ij} = C(\|s_i-s_j\|:\hat{\theta})\).
Volvemos a estimar \(\beta\) usando la matriz estimada \(\hat{\Sigma}\): \(\hat{\beta}_{GLS} = (X'\hat{\Sigma}^{-1}X)^{-1}X'\hat{\Sigma}^{-1}Y\)
Se puede proceder iterativamente y recalcular los residuales: \[\hat{\eta}(s_i)=Y(s_i)-X(s_i)'\hat{\beta}_{GLS}\] para después reètir 3 y 4.
8.3.3.2 Métodos de máxima verosimilitud
Los métodos de máxima verosimilitud implican supuestos ditrsibucionales, lo más común en estadística espacial es suponer que \(Y(s)\) es un proceso Gaussiano. Escribimos nuevamente:
\[ \begin{align} \nonumber Y(s) = \mu(s) + \eta(s)\\ \nonumber \mu(s) = X(s)'\beta \end{align} \]
de manera que \(\eta(s)\) se modela como un proceso Gaussiano de media cero y covarianza \(Cov(\eta(s'),\eta(s)) = C(s',s:\theta)\). Este supuesto implica \(Y \sim MVN(X\beta, \Sigma)\), y podemos escribir la verosimilitud: \[\mathcal{L} = \frac{1}{(2\pi)^{n/2}}\frac{1}{(\| \Sigma(\theta) \|^{1/2}}exp\left(-\frac{1}{2}(Y-X\beta)'\Sigma(\theta)^{-1}(Y-X\beta)\right)\] donde \(\Sigma(\theta)_{ij}=C(s_i,s_j:\theta)\).
De tal manera que buscamos estimar \(\beta\) y \(\theta\), esto no se puede hacer de manera directa por lo que utilizamos métodos iterativos (como Newton-Raphson, o el método de puntajes de Fisher).
Algunos aspectos importantes:
Podemos comparar la verosimilitud (o el AIC, BIC) de los modelos y tener así un criterio adicional para seleccionar el modelo paramétrico.
En el proceso iterativo de estimación podemos utilizar como valores iniciales \(\theta^{(0)}\) las estimaciones de geostadística clásica (WLS).
El MLE puede no existir, la función podría ser multimodal.
Es conveniente utilizar varios valores iniciales para evaluar la convergencia.
Las estimaciones de los parámetros de covarianza \(\theta\) son sesgados, y esto podría ser problemático en muestras chicas.
Una solución al problema del sesgo de \(\hat{\theta}\) es utilizar máxima verosimilitud restringida (REML), esta consiste en realizar la máxima verosimilitud en contrastes de \((Y_1,...,Y_n)\) en lugar de en los observados \((Y_1,...,Y_n)\). En la práctica se han observado mejoras en el sesgo; sin embargo, REML puede conllevar mayor error cuadrático medio comparado a máxima verosimilitud usual.
water.geo <- as.geodata(soil, coords.col = c(1,2), data.col = 7)
water.ml <- likfit(water.geo, trend = "1st", cov.model="spherical",
ini=c(sigma2.sph, phi.sph), nugget = tau2.sph, fix.nugget = FALSE,
lik.met="ML")
#> kappa not used for the spherical correlation function
#> ---------------------------------------------------------------
#> likfit: likelihood maximisation using the function optim.
#> likfit: Use control() to pass additional
#> arguments for the maximisation function.
#> For further details see documentation for optim.
#> likfit: It is highly advisable to run this function several
#> times with different initial values for the parameters.
#> likfit: WARNING: This step can be time demanding!
#> ---------------------------------------------------------------
#> likfit: end of numerical maximisation.
water.reml <- likfit(water.geo, trend = "1st", cov.model="spherical",
ini=c(sigma2.sph, phi.sph), nugget = tau2.sph, fix.nugget = FALSE,
lik.met="REML")
#> kappa not used for the spherical correlation function
#> ---------------------------------------------------------------
#> likfit: likelihood maximisation using the function optim.
#> likfit: Use control() to pass additional
#> arguments for the maximisation function.
#> For further details see documentation for optim.
#> likfit: It is highly advisable to run this function several
#> times with different initial values for the parameters.
#> likfit: WARNING: This step can be time demanding!
#> ---------------------------------------------------------------
#> likfit: end of numerical maximisation.
data.frame(method = c("Classical", "ML", "REML"),
sigma2 = c(sigma2.sph, water.ml$sigmasq, water.reml$sigmasq),
phi = c(phi.sph, water.ml$phi, water.reml$phi),
tau2 = c(tau2.sph, water.ml$tausq, water.reml$tausq),
AIC = c(NA, water.ml$AIC, water.reml$AIC),
BIC = c(NA, water.ml$BIC, water.reml$BIC))
#> method sigma2 phi tau2 AIC BIC
#> 1 Classical 0.03273520 20.94911 0.0009100885 NA NA
#> 2 ML 0.03174821 20.88569 0.0008669238 -339.2346 -318.1058
#> 3 REML 0.03386304 20.96128 0.0004101775 -340.3304 -319.2016 Compara el AIC y BIC del modelo con
polinomio de segundo grado para la tendencia contra el modelo con
polinomio de tercer grado.