8.4 Kriging: Predicción espacial
Dado un proceso espacial para el cual hemos recolectado datos en ubicaciones buscamos predecir una función condicional a los datos observados. Iniciemos con el caso simple , es decir, queremos predecir el valor del proceso en una nueva ubicación . Para hacer las estimaciones de utilizaremos un método de interpolación conocido como kriging.
Las características principales de kriging son:
Las ecuaciones de kriging reflejan que las observaciones se deben ponderar distinto: las observaciones cercanas a la predicción deben contribuir más.
La dependencia espacial está incluida en las ecuaciones de kriging por medio de los variogramas (o función de covarianzas).
Los valores interpolados se modean con un proceso Gaussiano.
Vamos a plantear el problema desde un enfoque de pérdida. Sea la predicción de y sea: la pérdida incurrida cuando predecimos usando , entonces un predictor óptimo es el que minimiza la pérdida esperada también conocida como riesgo de Bayes:
donde es el vector de observaciones de un proceso espacial .
Ahora, si escogemos como función de pérdida la pérdida cuadrática entonces el predictor que minimiza el riesgo de Bayes es: En general, no es fácil estimar , pero si es un proceso gaussiano es una función lineal de y kriging consiste en encontrar el parámetro tal que minimizando .
Hay tres tipos de kriging dependiendo de los supuestos que realicemos de la tendencia .
- Kriging simple. Suponemos que la tendencia espacial es conocida, suponemos además que conocemos la función de covarianza (incluyendo parámetros). Bajo estos supuestos, tiene la forma y se minimiza con: por lo tanto, el predictor lineal optimo de kriging simple es: donde y .
El error cuadrático medio de predicción (minimizado) es: se interpreta como la varianza de kriging y se utiliza para construir intervalos de confinaza de la predicción.
# supongamos que queremos predecir en x0, y0
x0 <- 13
y0 <- 13
# utilizaremos el objeto water.geo que creamos antes
# especificamos las opciones para el kriging, sk = simple kriging
kc.sk.control <- krige.control(type.krige = "sk", trend.d = "cte",
trend.l="cte",beta = 5.8, cov.model="spherical", cov.pars = c(0.02, 20.0),
nugget = 0.0001)
# Ponemos las coordenadas del punto en el que haremos kriging:
loc.sk <- matrix(c(x0,y0),nrow=1,ncol=2)
kc.sk.s0 <- krige.conv(water.geo,locations=loc.sk,krige=kc.sk.control)
#> krige.conv: model with constant mean
#> krige.conv: Kriging performed using global neighbourhood
kc.sk.s0$predict
#> data
#> 5.86531
kc.sk.s0$krige.var
#> [1] 0.004156077- Kriging ordinario. Suponemos que la tendencia espacial es consatnte y desconocida, suponemos además que conocemos la función de covarianza. El predictor lineal optimo de kriging ordinario se obtiene utilizando multiplicadores de Langrange, buscamos: sujeto a , la restricción adicional viene de la media desconocida pero constante, en este obtenemos tenemos:
# Primero estimaremos los parámetros usand WLS y covarinza esférica
# Vamos a estimar una media constante (aunque desconocida) por lo que no hace
# falta estimarla por separado, es decir usar lm
water.data <- data.frame(x = soil$x, y = soil$y, pH = soil$pH_water)
coordinates(water.data) = ~ x + y
emp.variog.water <- variogram(pH ~ 1, water.data)
plot(emp.variog.water)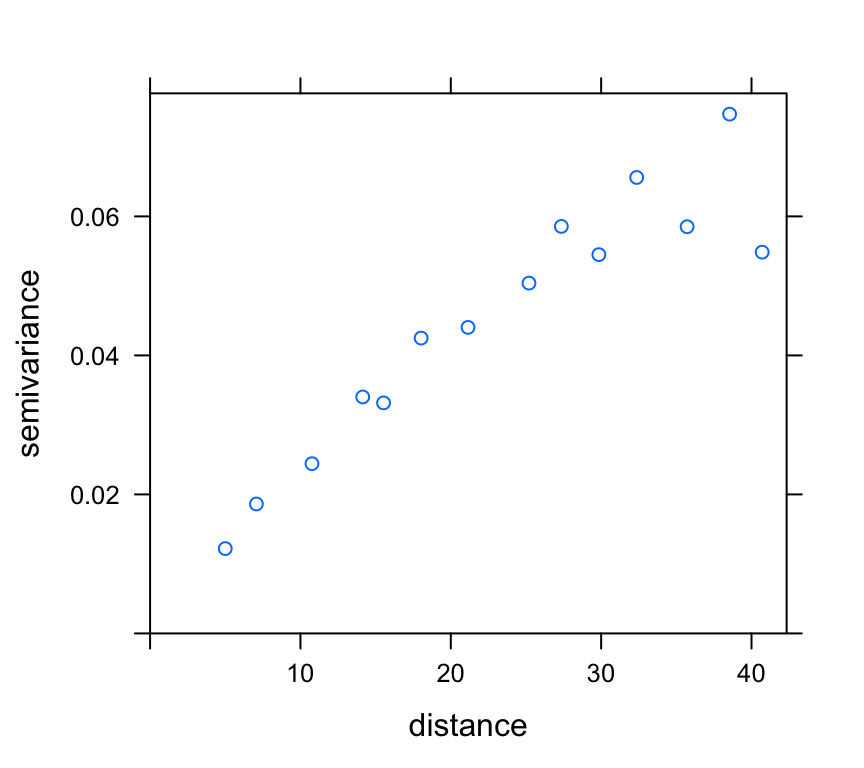
# Ajustamos un variograma esférico usando WLS
sph.variog.water <- fit.variogram(emp.variog.water, vgm(psill=0.01, "Sph",
range=35, nugget = 0.01), fit.method = 2)
sph.variog.water
#> model psill range
#> 1 Nug 8.022807e-05 0.00000
#> 2 Sph 6.145727e-02 38.70891
sigma2.wls <- sph.variog.water$psill[2]
phi.wls <- sph.variog.water$range[2]
tau2.wls <- sph.variog.water$psill[1]
# especificamos las opciones para el kriging, ok = ordinary kriging
kc.ok.control <- krige.control(type.krige = "ok", trend.d = "cte",
trend.l = "cte", cov.model = "spherical", cov.pars=c(sigma2.wls, phi.wls),
nugget = tau2.wls)
# Ponemos las coordenadas del punto en el que haremos kriging:
loc.ok <- matrix(c(x0,y0),nrow=1,ncol=2)
kc.ok.s0 <- krige.conv(water.geo, locations = loc.ok, krige = kc.ok.control)
#> krige.conv: model with constant mean
#> krige.conv: Kriging performed using global neighbourhood
kc.ok.s0$predict
#> data
#> 5.877374
kc.ok.s0$krige.var
#> [1] 0.006511266- Kriging universal. Suponemos que la tendencia espacial es desconocida de la forma donde es un vector con covariables y es el vector de parámetros desconocidos. Suponemos además que conocemos la función de covarianza. Entonces, minimizando con multiplicadores de Lagrange: sujeto a y obtenemos:
# Primero ajustamos un modelo lineal a los datos para obtener los residuales eta.hat
mod.water.lin <- lm(pH_water ~ x + y, data = soil)
trend.water.lin <- mod.water.lin$fitted.values
res.water.lin <- soil$pH_water - trend.water.lin
# Derivamos la estimación WLS del semivariograma esférico
water.res.data <- data.frame(x = soil$x, y = soil$y, res.water.lin = res.water.lin)
coordinates(water.res.data) = ~ x + y
emp.variog.res.water <- variogram(res.water.lin ~ 1, water.res.data)
plot(emp.variog.res.water)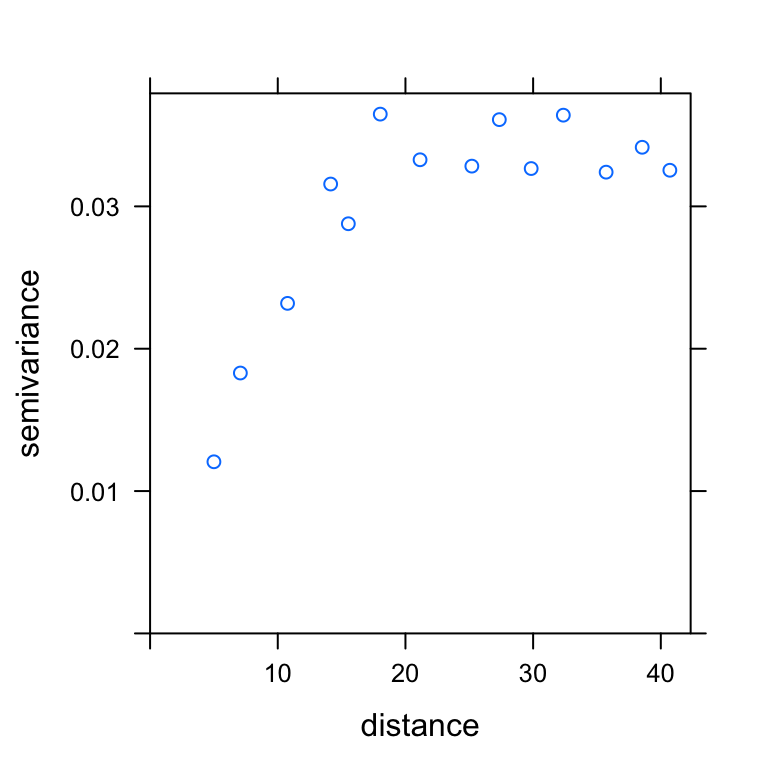
sph.variog.res.water <- fit.variogram(emp.variog.res.water, vgm(psill = 0.03,
"Sph", range = 15, nugget = 0.012), fit.method = 2)
sigma2.sph <- sph.variog.res.water$psill[2]
phi.sph <- sph.variog.res.water$range[2]
tau2.sph <- sph.variog.res.water$psill[1]
# Calculamos las estimaciones REML
water.reml.sph <- likfit(water.geo, trend = ~ soil$x + soil$y,
cov.model="spherical",ini=c(sigma2.sph, phi.sph), nugget=tau2.sph,
fix.nug = FALSE, lik.met="REML")
#> kappa not used for the spherical correlation function
#> ---------------------------------------------------------------
#> likfit: likelihood maximisation using the function optim.
#> likfit: Use control() to pass additional
#> arguments for the maximisation function.
#> For further details see documentation for optim.
#> likfit: It is highly advisable to run this function several
#> times with different initial values for the parameters.
#> likfit: WARNING: This step can be time demanding!
#> ---------------------------------------------------------------
#> likfit: end of numerical maximisation.
water.reml.sph
#> likfit: estimated model parameters:
#> beta0 beta1 beta2 tausq sigmasq phi
#> " 5.9083" "-0.0073" " 0.0000" " 0.0004" " 0.0339" "20.9611"
#> Practical Range with cor=0.05 for asymptotic range: 20.9611
#>
#> likfit: maximised log-likelihood = 176.2
sigma2.reml <- water.reml.sph$sigmasq
phi.reml <- water.reml.sph$phi
tau2.reml <- water.reml.sph$tausq
# Definimos los parámetros para universal kriging
# Como estamos asumiendo un polinomio lineal como tendencia cambiamos el
# valor de trend.d trend.l
kc.uk.control <- krige.control(type.krige = "ok", trend.d = "1st",
trend.l = "1st", cov.model = "spherical",
cov.pars=c(sigma2.reml, phi.reml), nugget = tau2.reml)
loc.uk <- matrix(c(x0,y0), nrow=1, ncol=2)
kc.uk.s0 <- krige.conv(water.geo,locations=loc.uk,krige=kc.uk.control)
#> krige.conv: model with mean given by a 1st order polynomial on the coordinates
#> krige.conv: Kriging performed using global neighbourhood
# estimaciones de beta:
kc.uk.s0$beta.est
#> beta0 beta1 beta2
#> 5.9083062496 -0.0073430647 -0.0000203476
# predicción
kc.uk.s0$predict
#> data
#> 5.865464
kc.uk.s0$krige.var
#> [1] 0.007055365
# Predecimos en un grid
x <- seq(0, 45, 1)
y <- seq(0, 120, 1)
grid.xy <- expand.grid(list(x, y))
head(grid.xy)
#> Var1 Var2
#> 1 0 0
#> 2 1 0
#> 3 2 0
#> 4 3 0
#> 5 4 0
#> 6 5 0
kc.uk.grid <- krige.conv(water.geo,locations=grid.xy,krige=kc.uk.control)
#> krige.conv: model with mean given by a 1st order polynomial on the coordinates
#> krige.conv: Kriging performed using global neighbourhood
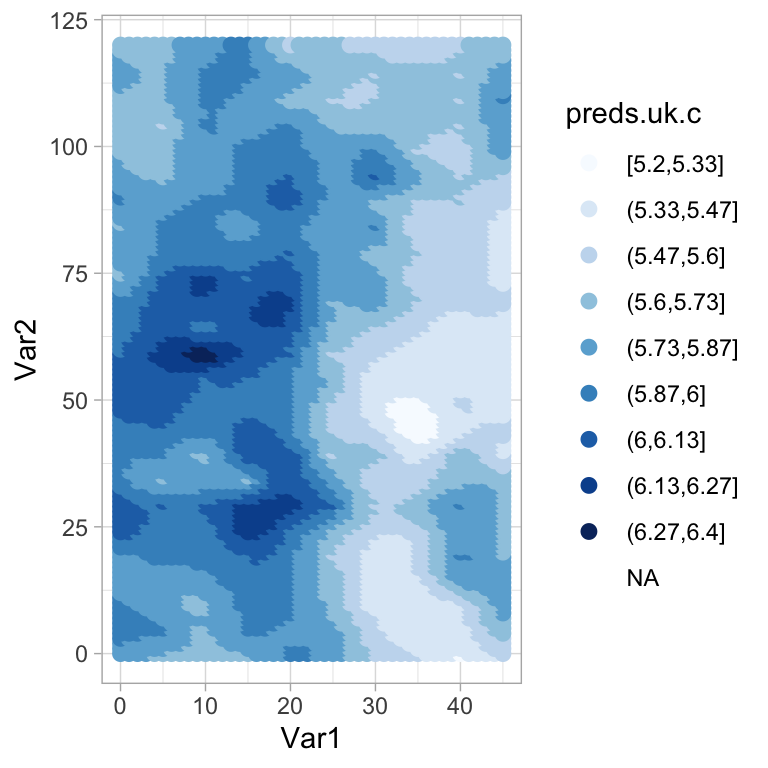
grid.xy$preds.uk <- kc.uk.grid$predict
grid.xy$preds.uk.c <- cut(grid.xy$preds.uk, class.ph$brks, include.lowest = TRUE)
ggplot(grid.xy, aes(x = Var1, y = Var2, colour = preds.uk.c)) +
geom_point(size = 2.3) +
scale_colour_brewer(palette = "Blues")