3.4 Comparación entre modelos gráficos dirigidos y no dirigidos
Hemos estudiado dos tipos de modelos gráficos, cada uno tiene distintos puntos fuertes y débiles:
- Especificar un modelo gráfico no dirigido es fácil (producto normalizado de
potenciales), sin embargo los factores no tienen interpretación probabilística.
Especificar un modelo gráfico dirigido es difícil (necesitamos escoger un
ordenamiento de las variables), pero en este caso los factores son densidades de
probabilidad marginales.
- Determinar independencias en modelos no dirigidos es fácil (separación) y en
modelos dirigidos es difícil (d-separación).
- Los modelos dirigidos y no dirigidos son lenguajes distintos, hay densidades
con propiedades de independencia que sólo se pueden describir con modelos
dirigidos (colisionadores) y lo mismo es cierto para no dirigidos (diamante).
- A pesar de estas diferencias, la inferencia en modelos dirigidos usualmente comienza por convertirlos en modelos no dirigidos con menos independencias condicionales.
Ahora veremos como se relacionan las redes bayesianas y las redes markovianas, para ello veremos como pasar de un tipo de modelo al otro.
3.4.1 Redes Bayesianas a Redes Markovianas
Podemos ver la relación entre redes Bayesianas y Markovianas desde dos perspectivas: 1) Dada una red Bayesiana \({\mathcal B}\) como representar la distribución \(p_{\mathcal B}\) como una parametrización correspondiente a una red markoviana, o 2) Dada una gráfica dirigida \({\mathcal G}\) como represento las indepencias en \({\mathcal G}\) usando una gráfica no dirigida \({\mathcal H}\).
Respecto al primer punto, es fácil notar que las densidades marginales y condicionales que definen una red bayesiana son potenciales, por tanto una factorización de una gráfica dirigida en densidades condicionales corresponde a una factorización de una distribución de Gibbs donde la constante de normalización es \(Z=1\).
En cuanto a la representación gráfica, para transformar una red bayesiana en una red markoviana definimos un clique sobre cada familia (cada nodo y sus padres) en la red bayesiana. Definir un clique sobre cada familia corresponde en la gráfica a conectar los padres de cada nodo (en caso de que no exista esta arista) y eliminar la dirección de las aristas. El proceso de transformar una red bayesiana en una red markoviana se conoce como moralización debido a que se casan (o conectan) los padres de una variable, la definición formal es:
La gráfica moral \({\mathcal M[G]}\) de una red Bayesiana con estructura \({\mathcal G}\) sobre \(V\) (conjunto de nodos/variables aleatorias) es una gráfica no dirigida sobre \(V\) que contiene una arista entre \(X\) y \(Y\) si: a) hay una arista dirigida entre ellas (sin importar la dirección), ó b) \(X\) y \(Y\) son padres del mismo nodo.
Un corolario de la definición anterior es que si \({\mathcal G}\) es la estructura de una red bayesiana, entonces para cualquier distribución \(p_{\mathcal B}\) tal que \({\mathcal B}\) es una parametrización de \({\mathcal G}\), tenemos que \({\mathcal M[G]}\) es un mapeo de las independencias de \(p_{\mathcal B}\).
Ejemplo
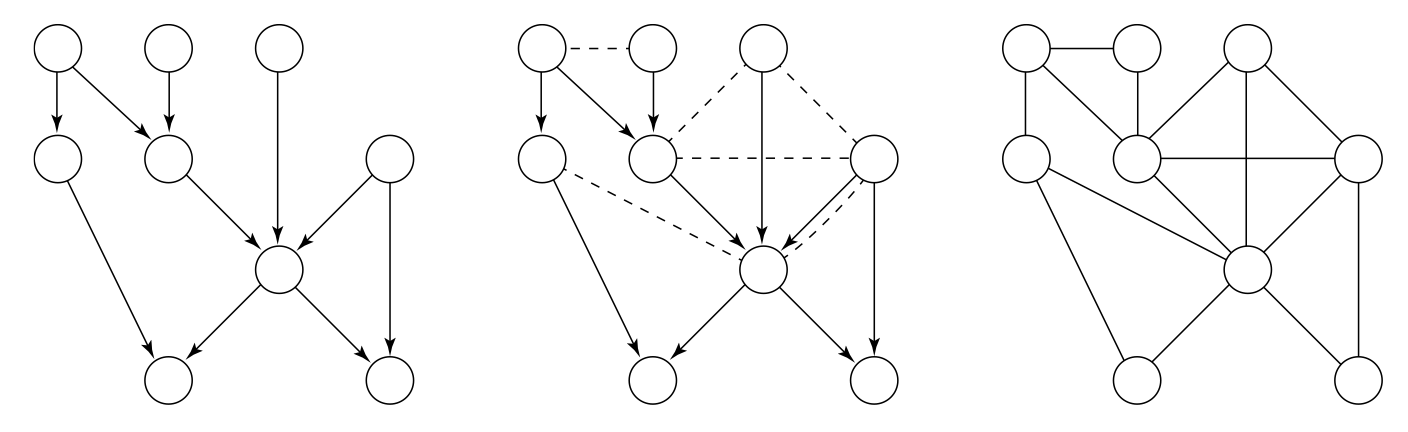 Notemos que todas las independencias condicionales que se representan en la
gráfica no dirigida también se leen en la gráfica dirigida, sin embargo, hay
independencias condicionales en el modelo dirigido que no se representan en el
modelo no dirigido. ¿Qué independencias implicadas en la red Bayesiana hemos
perdido al moralizar la gráfica?
Notemos que todas las independencias condicionales que se representan en la
gráfica no dirigida también se leen en la gráfica dirigida, sin embargo, hay
independencias condicionales en el modelo dirigido que no se representan en el
modelo no dirigido. ¿Qué independencias implicadas en la red Bayesiana hemos
perdido al moralizar la gráfica?
Del ejemplo anterior concluímos que el proceso de moralizar una gráfica dirigida puede conllevar que perdamos información de independencias; sin embargo, la siguiente proposición implica que moralizar es un mecanismo adecuado para transformar una gráfica dirigida en una no dirigida.
Sea \({\mathcal G}\) una gráfica asociada a una red Bayesiana. La gráfica moralizada \({\mathcal M[G]}\) es un mapeo mínimo de las independencias de \({\mathcal G}\).
La proposición anterior nos dice que si eliminamos una arista de \({\mathcal M[G]}\) estaríamos implicando relaciones de independencia que no se leen de la gráfica \({\mathcal G}\) y si añadimos aristas estaríamos perdiendo información de independencias de \({\mathcal G}\) que si se representan en \({\mathcal M[G]}\).
Vale la pena destacar que no siempre hay pérdida de información al moralizar una gráfica dirigida \({\mathcal G}\). Intuitivamente, la pérdida de información ocurre cuando se añaden aristas para conectar nodos, decimos que una red Bayesiana es moral si para cada par de variables \(X\), \(Y\) que comparten un hijo, existe una arista que une a \(X\) y \(Y\).
Si la gráfica dirigida \({\mathcal G}\) es moral, entonces su gráfica moralizada \({\mathcal M[G]}\) es un mapeo perfecto de \({\mathcal G}\). Esto es, todas las independencias que leemos en \({\mathcal G}\) se leen también en \({\mathcal M[G]}\).
Otra manera de leer este resultado es que las independencias en \({\mathcal G}\) que no estan presentes en la gráfica no dirigida que contiene las mismas aristas son las correspondientes a estructuras \(v\), a menos que la estructura \(v\) este protegida, en este último caso la gráfica dirigida no induce indepencias que no se lean también de la gráfica no dirigida.
3.4.2 Redes Markovianas a Redes Bayesianas
Consideremos ahora el problema de encontrar una red Bayesiana que se un mapeo minimal de las independencias de la red Markoviana. Veremos que en general la transformación en esta dirección es considerablemente más difícil.
Ejemplo
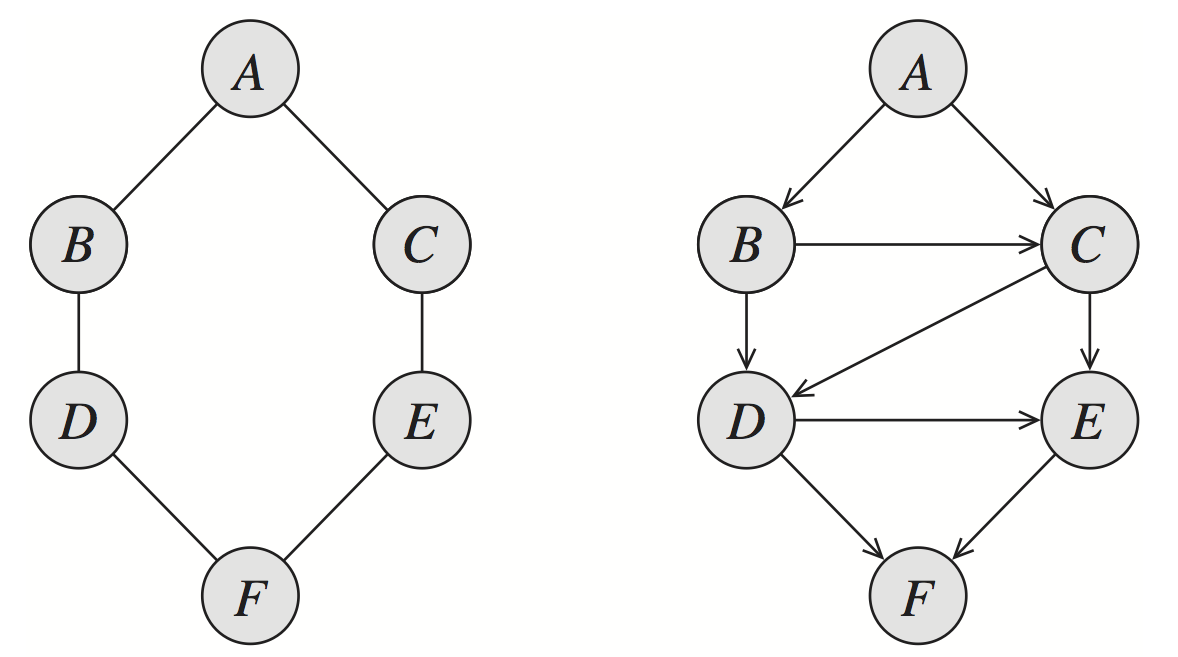
Consideremos la estructura de la red Markoviana de la figura de arriba y supongamos que buscamos una mapeo de esta red en una red bayesiana. Una manera es enumerar los nodos de la red y definir los padres de cada nodo en términos de las relacones de independencia que se leen de la red markoviana. Ordenemos los nodos de la siguiente manera: \(A,B,C,D,E,F\), la relación entre \(A\) y \(B\) es fácil, pero veamos que ocurre cuando añadimos a \(C\), introducimos \(A\) como padre de \(C\) pues no son independientes; sin embargo \(C\) tampoco es independiente de \(B\) condicional a \(A\) por lo que debemos añadir a \(B\) como padre de \(C\). Similarmemte consideramos \(D,E,F\) hasta obtener la gráfica dirigida de la derecha.
Es claro que hemos introducido aristas hasta formar una gráfica cordal (todos los ciclos están particionados en triángulos). Nos podemos preguntar si otro ordenamiento de los nodos podría conllevar introducir menos aristas, pero la respuesta es no: cualquier I-mapeo de una red Bayesiana que represente a la red markoviana debe introducir aristas que triangulan la gráfica produciendo una gráfica cordal.
Sea \({\mathcal H}\) una estructura de red Markoviana, y sea \({\mathcal G}\) una red bayesiana tal que es un mapeo minimal de las independencias de \({\mathcal H}\). Entonces \({\mathcal G}\) no puede tener inmoralidades.
Un corolario del teorema anterior es que \({\mathcal G}\) es necesariamente cordal. Esto se debe al proceso de triangulación que se requiere para convertir la red markoviana en red bayesiana.
En la transformación de una red no dirigda en una dirigida también perdemos información de independencias al introduci aristas. Volviendo al ejemplo anterior ¿Que relaciones de independencia se leen en la gráfica markoviana que no podemos leer en la red bayesiana?
3.4.3 Gráficas cordales
Hemos visto que la conversión entre redes bayesianas y markovianas puede resultar en la introducción de aristas que conlleva pérdida de informacióon de independencias implicada por la estructura de la gráfica original. Es interesante preguntarnos, ¿Cuándo un conjunto de supuestos de independencia se puede representar de manera perfecta usando ya sea una red markoviana o una red bayesiana? Resulta que esta es la clase de las gráficas cordales no dirigidas.
Sea \({\mathcal H}\) una red markoviana no cordal. Entonces no existe una red Bayesiana \({\mathcal G}\) que sea un mapeo perfecto de \({\mathcal H}\), esto es, no existe una red bayesiana de cuya gráfica se puedan leer todas las independencias que se leen de la red markoviana.