9.5 MCMC
Hay ocasiones en las que los métodos de inicial conjugada y aproximación por cuadrícula no funcionan, hay casos en los que la distribución beta no describe nuestras creencias iniciales. Por su parte, la aproximación por cuadrícula no es factible cuando tenemos varios parámetros. Es por ello que surge la necesidad de utilizar métodos de Monte Carlo vía Cadenas de Markov (MCMC).
Introducción Metrópolis
Para usar Metrópolis debemos poder calcular \(p(\theta)\) para un valor particular de \(\theta\) y el valor de la verosimilitud \(p(x|\theta)\) para cualquier \(x\), \(\theta\) dados. En realidad, el método únicamente requiere que se pueda calcular el producto de la inicial y la verosimilitud, y sólo hasta una constante de proporcionalidad. Lo que el método produce es una aproximación de la distribución posterior \(p(\theta|x)\) mediante una muestra de valores \(\theta\) obtenido de dicha distribución.
Caminata aleatoria. Con el fin de entender el algoritmo comenzaremos estudiando el concepto de caminata aleatoria. Supongamos que un vendedor de yakult trabaja a lo largo de una cadena de islas:
constantemente viaja entre las islas ofreciendo sus productos,
al final de un día de trabajo decide si permanece en la misma isla o se transporta a una de las \(2\) islas vecinas.
El vendedor ignora la distribución de la población en las islas y el número total de islasx; sin embargo, una vez que se encuentra en una isla puede investigar la población de la misma y también de la isla a la que se propone viajar después.
- El objetivo del vendedor es visitar las islas de manera proporcional a la
población de cada una. Con esto en mente el vendedor utiliza el siguiente
proceso:
- Lanza un volado, si el resultado es águila se propone ir a la isla del lado izquierdo de su ubicación actual y si es sol a la del lado derecho.
- Si la isla propuesta en el paso anterior tiene población mayor a la población de la isla actual, el vendedor decide viajar a ella. Si la isla vecina tiene población menor, entonces visita la isla propuesta con una probabilidad que depende de la población de las islas. Sea \(P_{prop}\) la población de la isla propuesta y \(P_{actual}\) la población de la isla actual. Entonces el vendedor cambia de isla con probabilidad \[p_{mover}=P_{prop}/P_{actual}\]
A la larga, si el vendedor sigue la heurística anterior la probabilidad de que el vendedor este en alguna de las islas coincide con la población relativa de la isla.
islas <- data.frame(islas = 1:10, pob = 1:10)
caminaIsla <- function(i){ # i: isla actual
u <- runif(1) # volado
v <- ifelse(u < 0.5, i - 1, i + 1) # isla vecina (índice)
if(v < 1 | v > 10){ # si estas en los extremos y el volado indica salir
return(i)
}
u2 <- runif(1)
p_move = min(islas$pob[v] / islas$pob[i], 1)
if(p_move > u2){
return(v) # isla destino
}
else{
return(i) # me quedo en la misma isla
}
}
pasos <- 100000
camino <- numeric(pasos)
camino[1] <- sample(1:10, 1) # isla inicial
for(j in 2:pasos){
camino[j] <- caminaIsla(camino[j - 1])
}
caminata <- data_frame(pasos = 1:pasos, isla = camino)
plot_caminata <- ggplot(caminata[1: 1000, ], aes(x = pasos, y = isla)) +
geom_point(size = 0.8) +
geom_path(alpha = 0.5) +
coord_flip() +
labs(title = "Caminata aleatoria") +
scale_y_continuous(expression(theta), breaks = 1:10) +
scale_x_continuous("Tiempo")
plot_dist <- ggplot(caminata, aes(x = isla)) +
geom_histogram() +
scale_x_continuous(expression(theta), breaks = 1:10) +
labs(title = "Distribución objetivo",
y = expression(P(theta)))
grid.arrange(plot_caminata, plot_dist, ncol = 1, heights = c(4, 2))
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.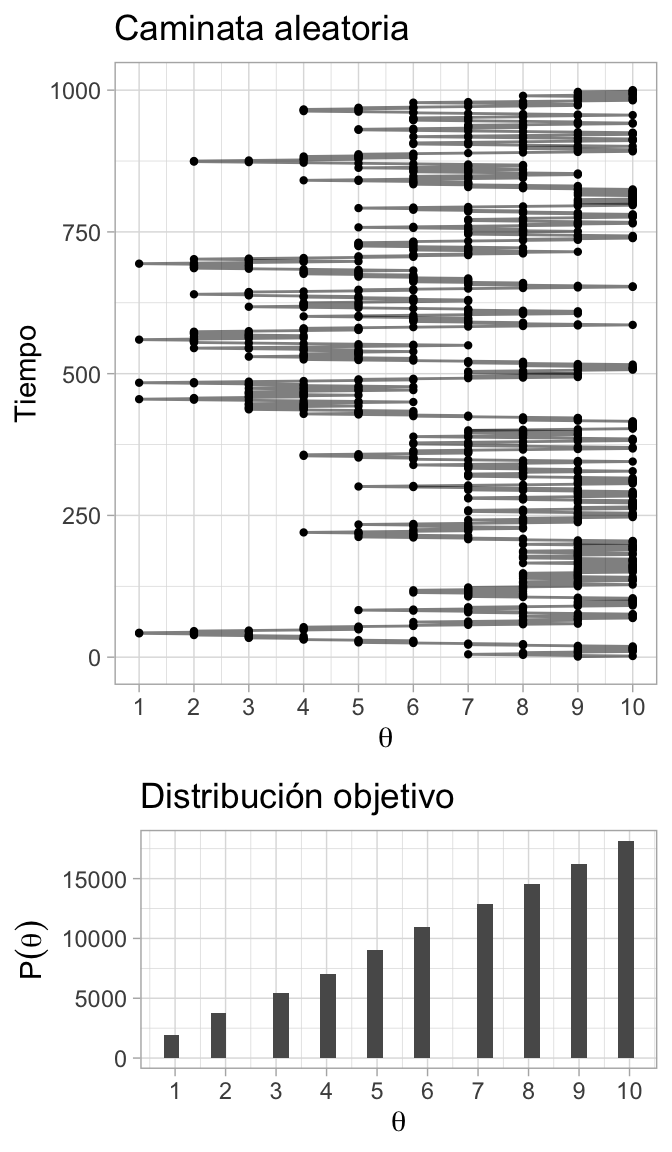
Entonces:
Para aproximar la distribución objetivo debemos permitir que el vendedor recorra las islas durante una sucesión larga de pasos y registramos sus visitas.
Nuestra aproximación de la distribución es justamente el registro de sus visitas.
Más aún, debemos tener cuidado y excluir la porción de las visitas que se encuentran bajo la influencia de la posición inicial. Esto es, debemos excluir el periodo de calentamiento.
Una vez que tenemos un registro largo de los viajes del vendedor (excluyendo el calentamiento) podemos aproximar la distribución objetivo de cada valor de \(\theta\) simplemente contando el número relativo de veces que el vendedor visitó dicha isla.
t <- c(1:10, 20, 50, 100, 200, 1000, 5000)
plots_list <- lapply(t, function(i){
ggplot(caminata[1:i, ], aes(x = isla)) +
geom_histogram() +
labs(y = "", x = "", title = paste("t = ", i, sep = "")) +
scale_x_continuous(expression(theta), breaks = 1:10, limits = c(0, 11))
})
args.list <- c(plots_list,list(nrow=4,ncol=4))
invoke(grid.arrange, args.list)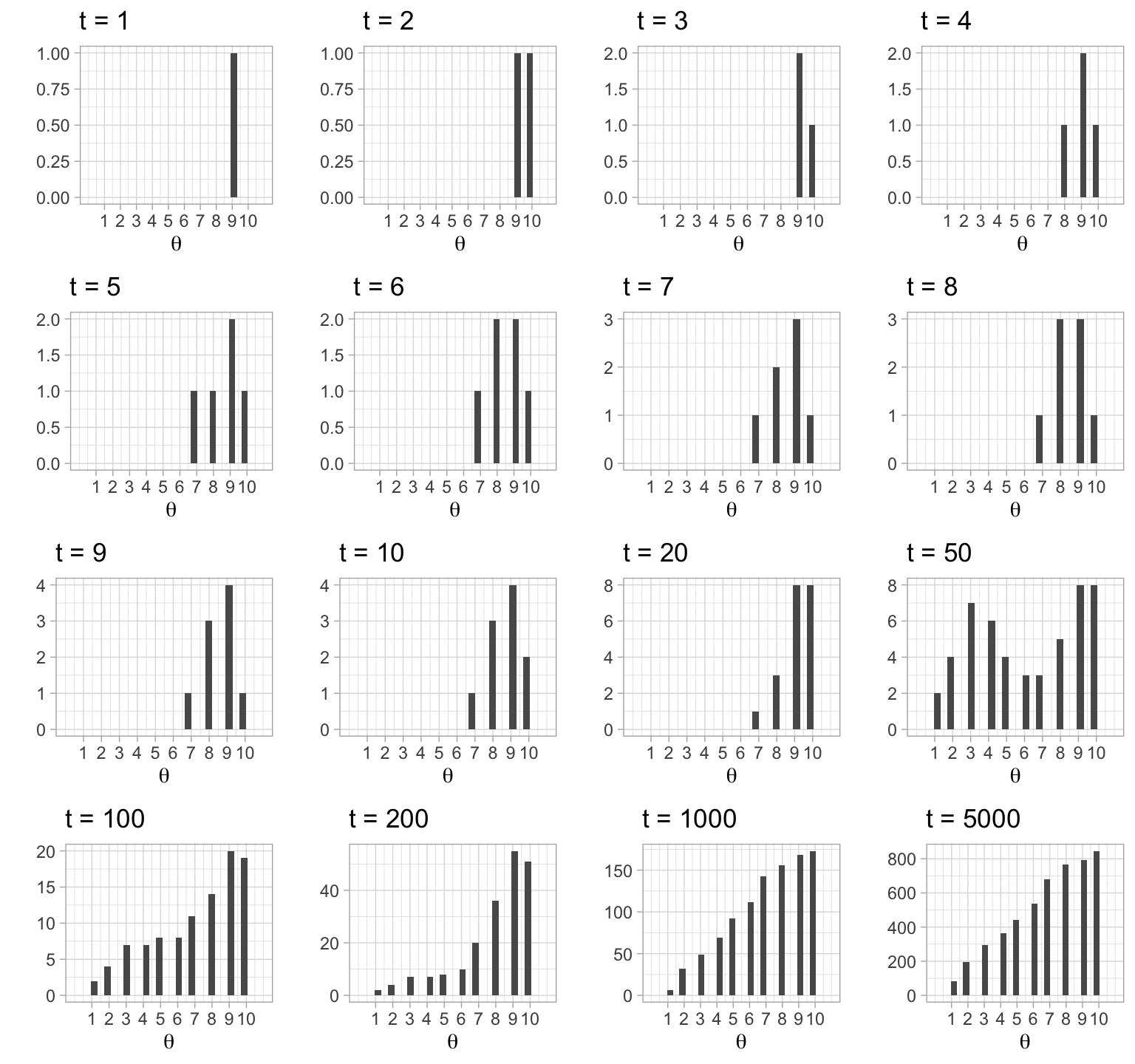
Escribamos el algoritmo, para esto indexamos las islas por el valor \(\theta\), es así que la isla del extremo oeste corresponde a \(\theta=1\) y la población relativa de cada isla es \(P(\theta)\):
El vendedor se ubica en \(\theta_{actual}\) y propone moverse a la izquierda o derecha con probabilidad \(0.5\).
El rango de los posibles valores para moverse, y la probabilidad de proponer cada uno se conoce como distribución propuesta, en nuestro ejemplo sólo toma dos valores cada uno con probabilidad \(0.5\).Una vez que se propone un movimiento, decidimos si aceptarlo. La decisión de aceptar se basa en el valor de la distribución objetivo en la posición propuesta, relativo al valor de la distribución objetivo en la posición actual: \[p_{mover}=min\bigg\{\frac{P(\theta_{propuesta})}{P(\theta_{actual})},1\bigg\}\] Notemos que la distribución objetivo \(P(\theta)\) no necesita estar normalizada, esto es porque lo que nos interesa es el cociente \(P(\theta_{propuesta})/P(\theta_{actual})\).
Una vez que propusimos un movimiento y calculamos la probabilidad de aceptar el movimiento aceptamos o rechazamos el movimiento generando un valor de una distribución uniforme, si dicho valor es menor a \(p_{mover}\) entonces hacemos el movimiento.
Entonces, para utilizar el algoritmo necesitamos ser capaces de:
Generar un valor de la distribución propuesta (para crear \(\theta_{propuesta}\)).
Evaluar la distribución objetivo en cualquier valor propuesto (para calcular \(P(\theta_{propuesta})/P(\theta_{actual})\)).
Generar un valor uniforme (para movernos con probabilidad \(p_{mover}\))
Las \(3\) puntos anteriores nos permiten generar muestras aleatorias de la distribución objetivo, sin importar si esta está normalizada. Esta técnica es particularmente útil cuando cuando la distribución objetivo es una posterior proporcional a \(p(x|\theta)p(\theta)\).
Para entender porque funciona el algoritmo de Metrópolis hace falta entender \(2\) puntos, primero que la distribución objetivo es estable: si la probabilidad actual de ubicarse en una posición coincide con la probabilidad en la distribución objetivo, entonces el algoritmo preserva las probabilidades.
library(expm)
transMat <- function(P){ # recibe vector de probabilidades (o población)
T <- matrix(0, 10, 10)
n <- length(P - 1) # número de estados
for(j in 2:n - 1){ # llenamos por fila
T[j, j - 1] <- 0.5 * min(P[j - 1] / P[j], 1)
T[j, j] <- 0.5 * (1 - min(P[j - 1] / P[j], 1)) +
0.5 * (1 - min(P[j + 1] / P[j], 1))
T[j, j + 1] <- 0.5 * min(P[j + 1] / P[j], 1)
}
# faltan los casos j = 1 y j = n
T[1, 1] <- 0.5 + 0.5 * (1 - min(P[2] / P[1], 1))
T[1, 2] <- 0.5 * min(P[2] / P[1], 1)
T[n, n] <- 0.5 + 0.5 * (1 - min(P[n - 1] / P[n], 1))
T[n, n - 1] <- 0.5 * min(P[n - 1] / P[n], 1)
T
}
T <- transMat(islas$pob)
w <- c(0, 1, rep(0, 8))
t <- c(1:10, 20, 50, 100, 200, 1000, 5000)
expT <- map_df(t, ~data.frame(t = ., w %*% (T %^% .)))
expT_long <- expT %>%
gather(theta, P, -t) %>%
mutate(theta = parse_number(theta))
ggplot(expT_long, aes(x = theta, y = P)) +
geom_bar(stat = "identity", fill = "darkgray") +
facet_wrap(~ t) +
scale_x_continuous(expression(theta), breaks = 1:10, limits = c(0, 11))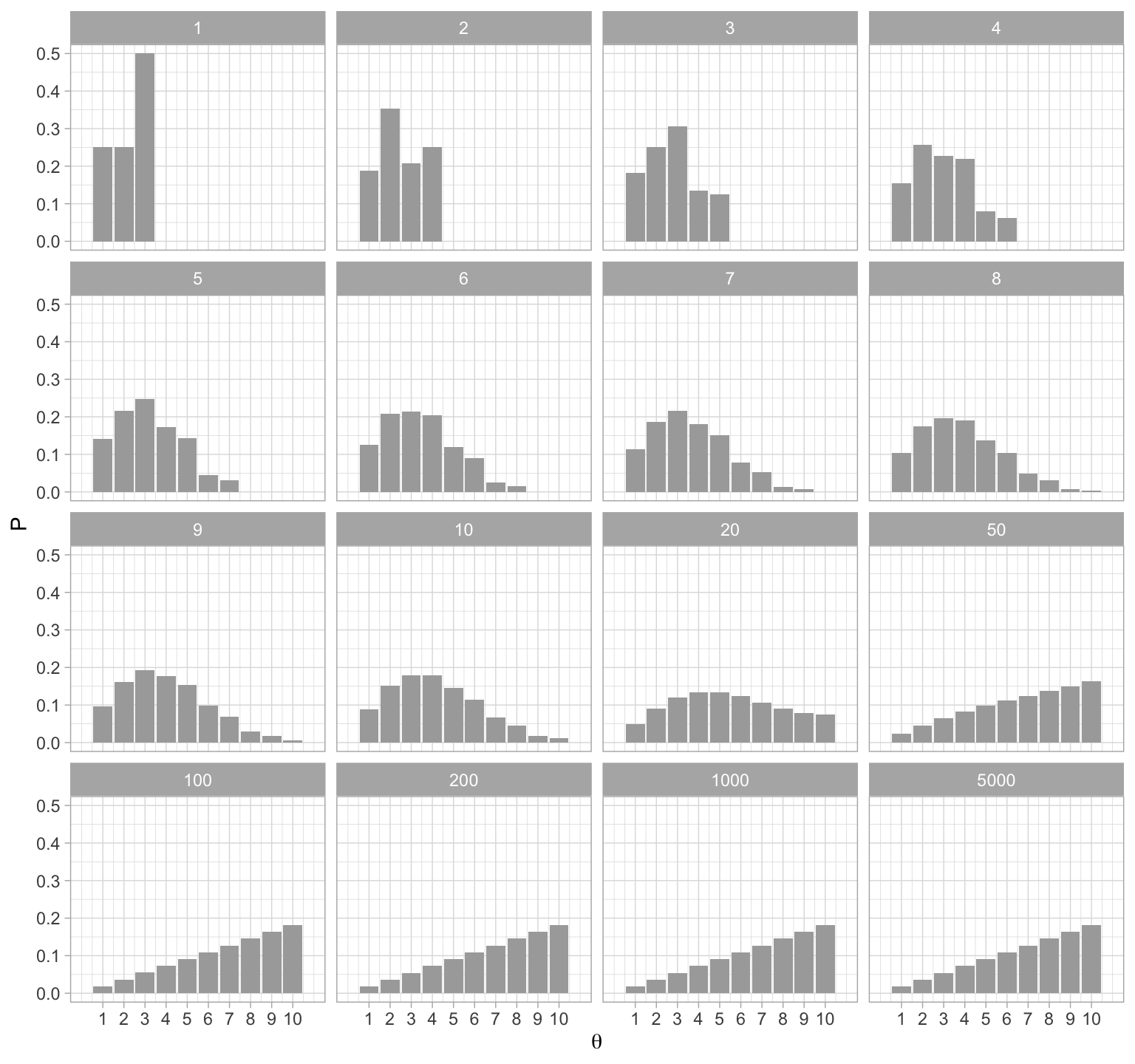
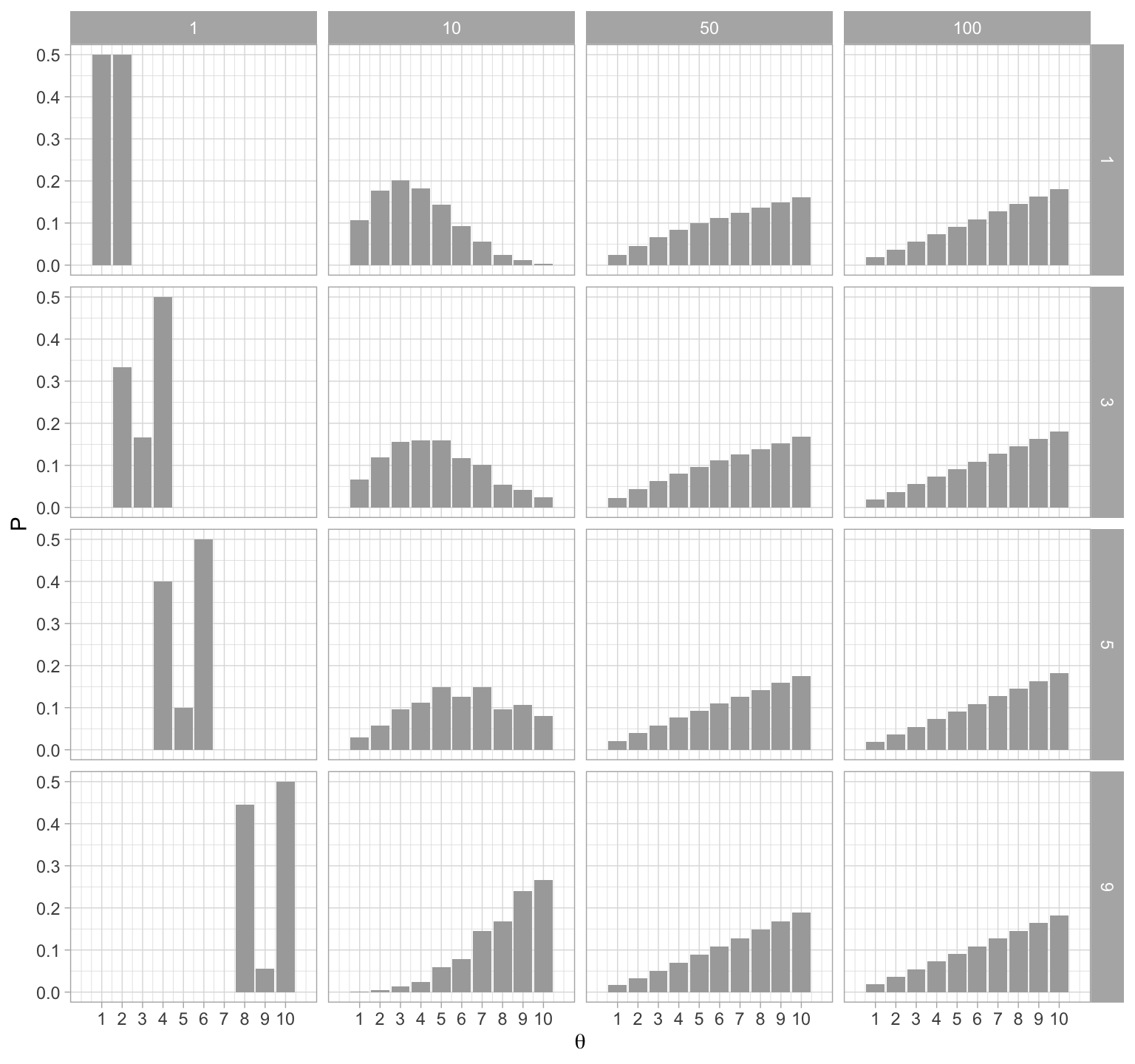
El segundo punto es que el proceso converge a la distribución objetivo. Podemos ver, (en nuestro ejemplo sencillo) que sin importar el punto de inicio se alcanza la distribución objetivo.
inicioP <- function(i){
w <- rep(0, 10)
w[i] <- 1
t <- c(1, 10, 50, 100)
expT <- map_df(t, ~data.frame(t = ., inicio = i, w %*% (T %^% .))) %>%
gather(theta, P, -t, -inicio) %>%
mutate(theta = parse_number(theta))
expT
}
expT <- map_df(c(1, 3, 5, 9), inicioP)
ggplot(expT, aes(x = as.numeric(theta), y = P)) +
geom_bar(stat = "identity", fill = "darkgray") +
facet_grid(inicio ~ t) +
scale_x_continuous(expression(theta), breaks = 1:10, limits = c(0, 11))