3.2 Representación log-lineal
Los modelos log-lineales han sido ampliamente utilizados en ciencias sociales para el análisis de tablas de contingencia, su desarrollo ha permitido formular y ajustar patrones de asociación complejas entre los dactores que cruzan en una tabla de contingencias.
Ejemplo. Usaremos la base de datos de lagartijas, tenemos \(N=409\) observaciones y \(d=3\) variables.
Un modelo log-lineal permite expresar el log de las probabilidades con expresiones de factoriales. Por ejemplo, para un modelo de saturado (donde se estiman parámetros para todos los cruces de factores) de 3 variables tenemos:
\[\log p(x) = u + u_X + u_Y + u_Z + u_{X,Y} + u_{X,Z} + u_{Y,Z} + u_{X,Y,Z} \]
donde las \(u\) son parámetros desconocidos.
En el ejemplo de lagartijas, si no restringimos las probabilidades del modelo (es decir, estimamos todos los cruces), tenemos un total de 8 parámetros (7 pues el último está dado), para cada parámetro la estimación de máxima verosimilitud es \(p_i=n_i/N\), esto es la proporción de observaciones en la celda i.
prop.table(lizard)
#> , , species = anoli
#>
#> height
#> diam >4.75 <=4.75
#> <=4 0.07823961 0.21026895
#> >4 0.02689487 0.08557457
#>
#> , , species = dist
#>
#> height
#> diam >4.75 <=4.75
#> <=4 0.14914425 0.17848411
#> >4 0.10024450 0.17114914Repetimos la estimación utilizando la representación log-lineal:
Los modelos log-lineales nos permiten hacer cero algunas interacciones, por ejemplo podemos ajustar:
\[\log p(x) = u + u_X + u_Y + u_Z + u_{X,Y} + u_{X,Z} \]
En las siguientes secciones estudiaremos la relación entre una clase de modelos log-lineales y redes markovianas.
3.2.1 Modelos gráficos log-lineales
Recordemos que algunos de los resultados de redes markovianas se sostenían únicamente para conjuntas positivas, por lo que podemos restringirnos a este conjunto y por tanto podemos representarlas de manera lgoarítmica de la siguiente forma:
Una distribución de Gibbs sobre \(\mathcal M\) se escribe
\[p(x) \propto \prod_{c\in {\mathcal C}} \psi_c (x_c).\]
Si todos los factores son positivos \(\psi_c>0\), definimos \(u_c=\log (\psi_c)\) de manera que
\[p(x)\propto \prod_{c\in {\mathcal C}} \exp (u_c (x_c)).\] y \[p(x)= \frac{\prod_{c\in {\mathcal C}} \exp (u_c (x_c))}{Z},\] donde \[Z= \sum_{x} \exp \left( \sum_{c\in {\mathcal C}}^{} {u_c(x_c)} \right).\]
Podemos también escribir
\[\log (p(x)) = \sum_{c\in {\mathcal C}}^{} u_c(x_c) - \log Z\]
donde \(\log Z\) es una constante de normalización.
La última expresión corresponde a un modelo log-lineal. En el resto de esta discusión, consideraremos la expresión log lineal para la conjunta, y supongamos que tenemos tres variables binarias que toman los valores \(0,1\). Comenzamos con el modelo deindependencia (o solamente de efectos principales), que es
\[\log p(x) = u + u_X + u_Y + u_Z\]
donde \(u\) representa el término de normalización. Esta gráfica corresponde a la gráfica de \(X,Y,Z\) sin arcos. Nótese que esta expresión está sobreparametrizada (contiene 6 parámetros, pero la conjunta solo depende de 3 parámetros). Esto quiere decir que hay una infinidad de maneras de representar a una misma conjunta por medio de las \(u\). Este punto no es crucial, pero podríamos restringir a \(u_X(0)=u_Y(0)=u_Z(0)=0\) y así obtenemos otra vez 3 parámetros.
Ahora supongamos que queremos eliminar la independencia entre \(X\) y \(Z\). En lugar de reescribir la expresión (absorbiendo \(u_X\) y \(u_Z\) en un factor \(u_{X,Z}\)), agregamos un término a la expresión anterior:
\[\log p(x) = u + u_X + u_Y + u_Z + u_{X,Z}\]
\(u_{X,Z}\) tiene 4 parámetros (sobreparametrizada), pero podemos eliminar la sobreparametrización estableciendo por ejemplo \(u_{X,Z}(x,z)= 0\) si \(x=0\) o \(z=0\), con lo que nos queda 1 parámetro. En total, tenemos entonces 3+1=4 parámetros, que corresponde a 1 para la marginal de \(Z\) y \(3\) para la conjunta de \(X\) y \(Y\).
Ahora agregemos una nueva arista entre \(Z\) y \(Y\). Podemos escribir
\[\log p(x) = u + u_X + u_Y + u_Z + u_{X,Z} + u_{Y,Z}\]
que con la misma restricción \(u_{Y,Z}(y,z)=0\) cuando \(y=0\) o \(z=0\) resulta en 5 parámetros, que es el número correcto (pues la conjunta se puede parametrizar con 1 parámetro para la marginal de \(Z\), y la condicional de \((X,Y)\) dado \(Z\) solo requiere 4 parámetros en lugar de 6 debido a la independencia \(X\bot Y|Z\)).
Finalmente, ¿qué sucede cuando agregamos el arco entre \(X\) y \(Y\)?
\[\log p(x) = u + u_X + u_Y + u_Z + u_{X,Z} + u_{Y,Z} + u_{X,Y}+u_{X,Y,Z}.\]
Tenemos que agregar el último término para poder capturar todos los patrones de dependencia de la gráfica completa de \(X\), \(Y\),\(Z\), pues esta gráfica contiene un factor \(\psi(x,y,z)\). Nótese que si no agregamos este término \(u_{X,Y,Z}\), entonces terminaríamos con 6 parámetros, pero sabemos que para parametrizar cualquier conjunta requerimos 8-1=7 parámetros.
Así que el modelo \[\log p(x) = u + u_X + u_Y + u_Z + u_{X,Z} + u_{Y,Z} + u_{X,Y}\]
tiene restricciones adicionales a las del modelo con gráfica completa, pues \(u_{X,Y,Z}=0\). Este modelo es un modelo log-lineal (en la definición usual), pero no es un modelo log-lineal gráfico, pues expresa independencias que no se pueden leer de la gráfica.
A los términos \(u\) se les llama muchas veces términos de interacción.
Siguiendo el proceso de construcción de arriba el tipo de modelos que nos interesa es:
Un modelo log-lineal gráfico asociado a la gráfica \(\mathcal M\) es de la forma \[\log p(x) = u + \sum_i \phi_i^1 u_i + \sum_{i,j}\phi_{i,j}^2 u_{i,j}+\cdots + \sum_{i_1,\ldots, i_s} \phi_{i_1,\ldots, i_s}^s u_{i_1,\ldots, i_s}\] donde
Las \(\phi\) toman el valor 1 o 0.
El modelo es jerárquico: si un término \(\phi_{i_1,\ldots, i_t}=1\), entonces todos los términos \(\phi_A=1\) para todo \(A\subset {i_1,\ldots, i_t}\).
- Los términos más altos de la expresión coresponden a cliques en \(\mathcal M\).
Ejemplos
La expresión \[u+ u_X+ u_{YZ}\] no es jerárquica. No puede resultar de la construcción que hicimos arriba, y por lo tanto tampoco puede ser un modelo gráfico.
La expresión \[u+ u_X+ u_Y+u_Z + u_{XY} + u_{XYZ}\] no es jerárquica. No puede resultar de la construcción que hicimos arriba, y por lo tanto tampoco puede ser un modelo gráfico.
*La expresión \[u + u_X + u_Y + u_Z + u_{X,Z} + u_{Y,Z} + u_{X,Y}\] es un modelo jerárquico, pero no es gráfico, pues \(X,Y,Z\) forman un clique, así que el término \(u_{X,Y,Z}\) no puede restringirse a ser 0.
Considera
\[u+u_1+u_2+u_3+u_4+u_5+u_{12}+u_{23}+u_{25}+u_{35}+u_{34}+u_{45}\]
- Es un modelo gráfico
- Es un modelo jerárquico
- Ninguna de las anteriores
Observación: En primer lugar, nótese que sin la parametrización y las restricciones que mostramos arriba, no tienen mucho sentido preguntarse si un modelo es jerárquico, pues todos los términos de grado más bajo se pueden absorber en el de orden más alto. La pregunta sería entonces: ¿por qué no usar con esta parametrización modelos no jerárquicos? Podemos por ejemplo considerar el modelo (\(X\) y \(Y\) binarias): \[u+u_X+u_{X,Y}\] con la restricción de que \(u_X(0)=0\) y \(u_{X,Y}(0,y)=u_{X,Y}(x,0)=0\). Entonces nótese que se tiene que cumplir que \(p(0,0)=p(0,1)\). Es decir, bajo esta parametrización modelos no jerárquicos incluyen otras restricciones que no tienen qué ver con la independencia condicional. No es que estos modelos no sirvan o estén mal, sino que en este punto no nos interesa modelar ese tipo de restricciones. En la práctica, típicamente se usan modelos jerárquicos.
3.2.2 Ajuste de modelos loglineales
Igual que en la gráficas no dirigidas, podemos escribir de manera fácil la verosimilitud bajo ciertos valores de los factores \(u\) de datos observados:
\[loglik(\theta, {\mathcal L})=\sum_i \log p(\theta; x^{(i)}),\] donde \(log(p(\theta; x^{(i)})\) es la probabilidad de la observación \(x^{(i)}\) según el modelo dado por la factorización, y \(\theta\) incluye todos los parámetros de los factores.
La diferencia más importante es que en general, no podemos usar la descomposición que hicimos en redes bayesianas de la verosimilitud.
En redes bayesianas, podíamos descomponer la verosimilitud en factores que correspondían a modelos locales, y resolver por separado para cada modelo local. En redes markovianas esto no es posible por la presencia del factor de normalización (en el que intervienen todos los parámetros de los factores en el modelo).
Tomando en cuenta esta diferencia hay varias maneras de estimar una red markoviana, uno de los métdos consiste en realizar pruebas de independencia para inferir la estructura del modelo conjunto. Y otro en utilizar heurísticas para optimizar un criterio.
Recordemos que en general no seleccionamos modelos usando la log-verosimilitud, sino que usaremos el AIC para seleccionar modelos que exploramos mediante una heurística más simple: dada una gráfica inicial no dirigida, en cada paso buscamos la eliminación o agregación del arco que resulte en la mejor ganancia en AIC.
Comenzaremos por ejemplo del error en clase. Primero simulamos datos según los datos del ejemplo, con una variable de ruido adicional:
library(dplyr)
potencial <- expand.grid(d = c(0, 1), c = c(0, 1), b = c(0, 1), a = c(0, 1)) %>%
mutate(
valor = c(3e05, 3e5, 3e5, 30, 500, 500, 5e6, 500, 100, 1e6, 100, 100, 10,
1e5, 1e5, 1e5),
indice = 1:n(),
prob = valor/sum(valor)
)
set.seed(2805)
muestra <- sample_n(potencial, size = 3000, weight = prob, replace = T) %>%
select(d, c, b, a)
# añadimos una variable independiente
muestra$e <- sample(c(0, 1), 3000, replace=T)La función dmod sirve para especificar modelos log-lineales.
Para usar el AIC o BIC, ponemos manualmente el coeficiente de penalización (2 para AIC y \(\log N\) para BIC):
mod_misco <- stepwise(m_init, k = log(nrow(muestra)),
direction='forward', type='unrestricted')
mod_misco
#> Model: A dModel with 5 variables
#> -2logL : 10605.81 mdim : 9 aic : 10623.81
#> ideviance : 6050.51 idf : 4 bic : 10677.87
#> deviance : 15.28 df : 22
plot(mod_misco)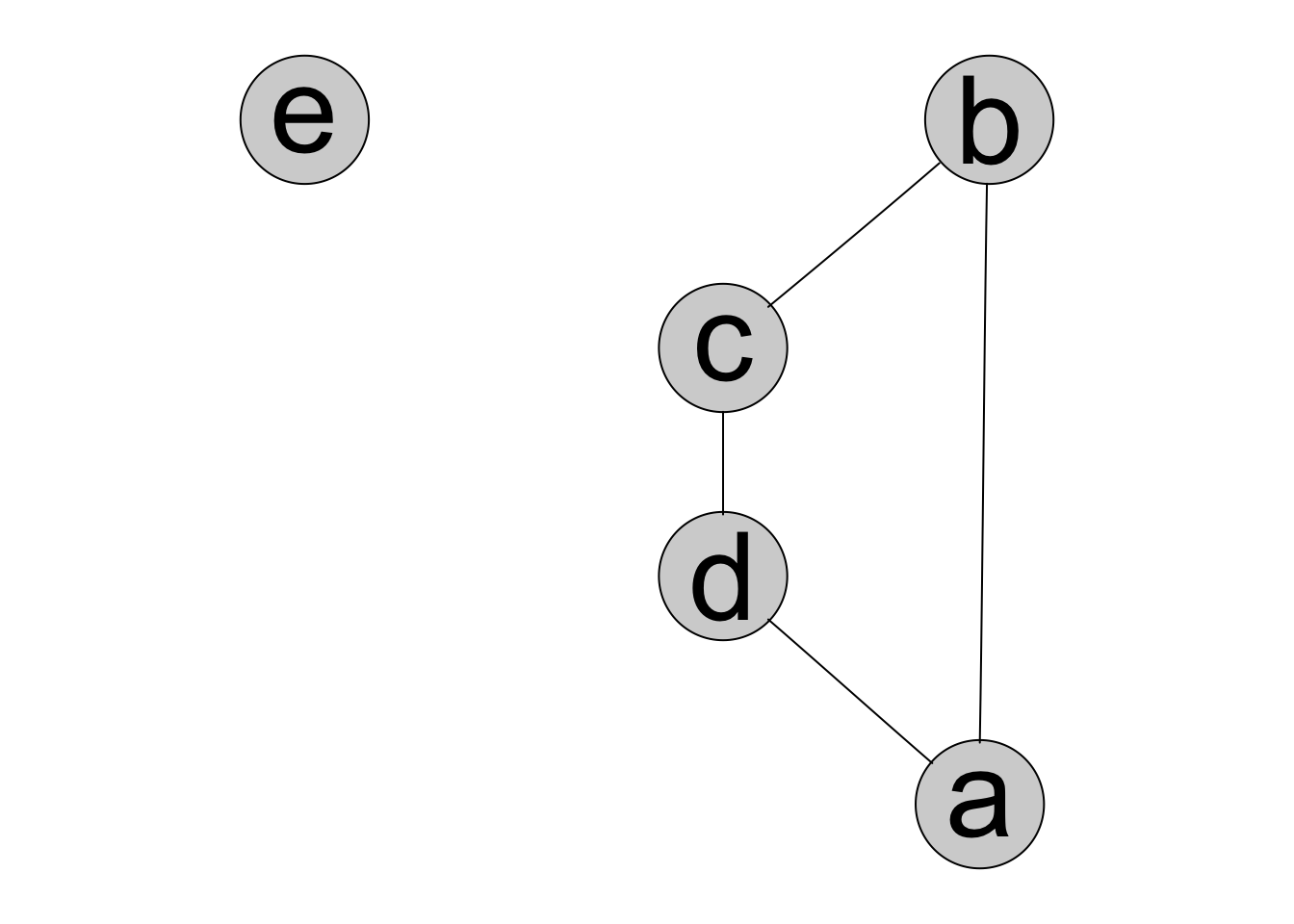
Las probabilidades ajustadas son (se puede omitir del cálculo en stepwise cuando es una tabla muy grande):
library(ggplot2)
ajuste <- mod_misco$datainfo
ajuste
#> $data
#> , , b = 0, a = 0, e = 0
#>
#> c
#> d 0 1
#> 0 61 58
#> 1 55 0
#>
#> , , b = 1, a = 0, e = 0
#>
#> c
#> d 0 1
#> 0 0 1046
#> 1 0 0
#>
#> , , b = 0, a = 1, e = 0
#>
#> c
#> d 0 1
#> 0 0 0
#> 1 214 0
#>
#> , , b = 1, a = 1, e = 0
#>
#> c
#> d 0 1
#> 0 0 24
#> 1 15 17
#>
#> , , b = 0, a = 0, e = 1
#>
#> c
#> d 0 1
#> 0 56 62
#> 1 66 0
#>
#> , , b = 1, a = 0, e = 1
#>
#> c
#> d 0 1
#> 0 0 1065
#> 1 1 0
#>
#> , , b = 0, a = 1, e = 1
#>
#> c
#> d 0 1
#> 0 0 0
#> 1 203 0
#>
#> , , b = 1, a = 1, e = 1
#>
#> c
#> d 0 1
#> 0 0 13
#> 1 16 28
ajuste_df <- data.frame(ajuste) %>%
rename_all(~stringr::str_replace(., "data.", "")) %>%
group_by(a, b, c, d) %>%
summarise(freq = sum(Freq)) %>%
ungroup() %>%
mutate(prob_aj = freq / sum(freq)) %>% # probabilidad ajustada
mutate_each(funs(as.numeric(as.character(.))), a:d)
# comparamos con las probabilidades originales
ej_comp <- inner_join(ajuste_df, potencial)
#> Joining, by = c("a", "b", "c", "d")
ggplot(ej_comp, aes(x = prob, y= prob_aj)) +
geom_abline(color = "red", alpha = 0.6) +
geom_point()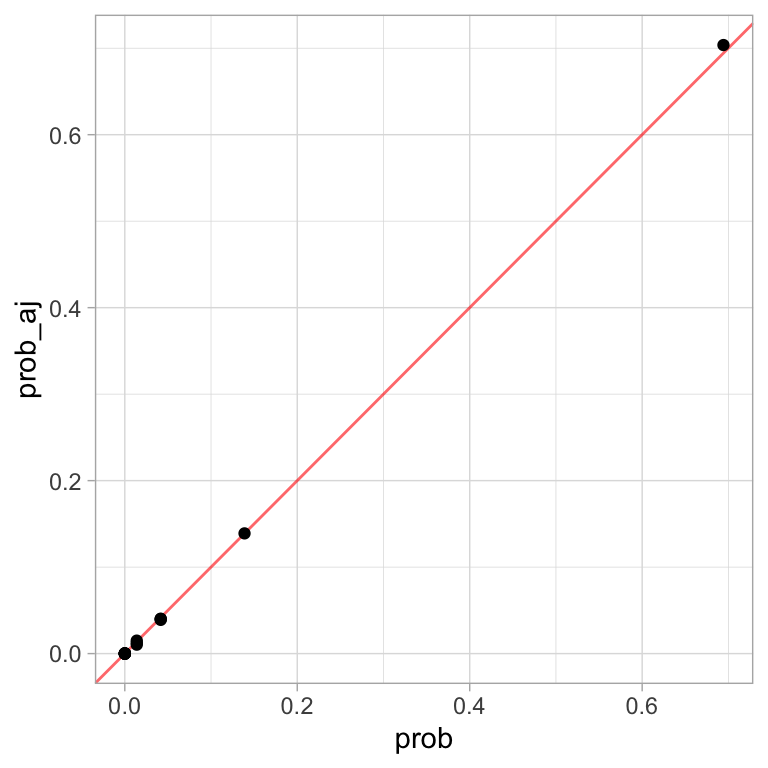 
En el siguiente ejemplo, seleccionamos un modelo para datos de riesgo de enfermedades del corazón. Tenemos 6 variables: fuma o no, si hace trabajo mental, si hace trabajo físico, si tiene presión baja, un indicador de colesterol alto, y un indicador de historia familiar de enfermedad del corazón:
library(gRim)
data(reinis)
reinis
#> , , phys = y, systol = y, protein = y, family = y
#>
#> mental
#> smoke y n
#> y 44 112
#> n 40 67
#>
#> , , phys = n, systol = y, protein = y, family = y
#>
#> mental
#> smoke y n
#> y 129 12
#> n 145 23
#>
#> , , phys = y, systol = n, protein = y, family = y
#>
#> mental
#> smoke y n
#> y 35 80
#> n 12 33
#>
#> , , phys = n, systol = n, protein = y, family = y
#>
#> mental
#> smoke y n
#> y 109 7
#> n 67 9
#>
#> , , phys = y, systol = y, protein = n, family = y
#>
#> mental
#> smoke y n
#> y 23 70
#> n 32 66
#>
#> , , phys = n, systol = y, protein = n, family = y
#>
#> mental
#> smoke y n
#> y 50 7
#> n 80 13
#>
#> , , phys = y, systol = n, protein = n, family = y
#>
#> mental
#> smoke y n
#> y 24 73
#> n 25 57
#>
#> , , phys = n, systol = n, protein = n, family = y
#>
#> mental
#> smoke y n
#> y 51 7
#> n 63 16
#>
#> , , phys = y, systol = y, protein = y, family = n
#>
#> mental
#> smoke y n
#> y 5 21
#> n 7 9
#>
#> , , phys = n, systol = y, protein = y, family = n
#>
#> mental
#> smoke y n
#> y 9 1
#> n 17 4
#>
#> , , phys = y, systol = n, protein = y, family = n
#>
#> mental
#> smoke y n
#> y 4 11
#> n 3 8
#>
#> , , phys = n, systol = n, protein = y, family = n
#>
#> mental
#> smoke y n
#> y 14 5
#> n 17 2
#>
#> , , phys = y, systol = y, protein = n, family = n
#>
#> mental
#> smoke y n
#> y 7 14
#> n 3 14
#>
#> , , phys = n, systol = y, protein = n, family = n
#>
#> mental
#> smoke y n
#> y 9 2
#> n 16 3
#>
#> , , phys = y, systol = n, protein = n, family = n
#>
#> mental
#> smoke y n
#> y 4 13
#> n 0 11
#>
#> , , phys = n, systol = n, protein = n, family = n
#>
#> mental
#> smoke y n
#> y 5 4
#> n 14 4
m_init <- dmod(~.^1 , data = reinis)
plot(m_init)
m_reinis <- stepwise(m_init, criterion = 'aic', details = T,
direction = 'forward', type = 'unrestricted')
#> STEPWISE:
#> criterion: aic ( k = 2 )
#> direction: forward
#> type : unrestricted
#> search : all
#> steps : 1000
#> change.AIC -683.9717 Edge added: mental phys
#> change.AIC -25.4810 Edge added: smoke phys
#> change.AIC -15.9293 Edge added: protein mental
#> change.AIC -38.4224 Edge added: smoke protein
#> change.AIC -23.6185 Edge added: systol protein
#> change.AIC -29.0833 Edge added: smoke systol
#> change.AIC -8.7290 Edge added: phys protein
#> change.AIC -2.7316 Edge added: family mental
plot(m_reinis)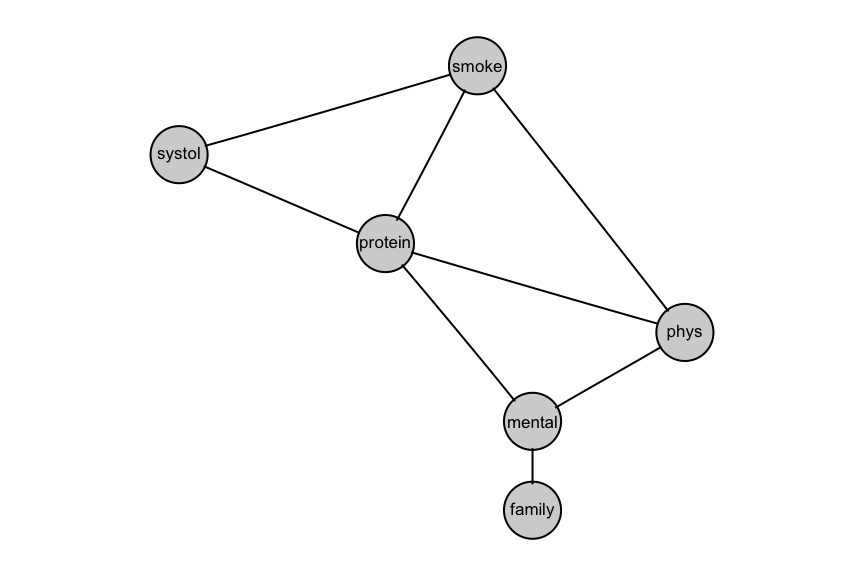
Un ejemplo simple con datos reales:
en este caso, queremos entender los patrones de variación de tres variables:
color de ojos, color de pelo y género.
data(HairEyeColor)
(HairEyeColor)
#> , , Sex = Male
#>
#> Eye
#> Hair Brown Blue Hazel Green
#> Black 32 11 10 3
#> Brown 53 50 25 15
#> Red 10 10 7 7
#> Blond 3 30 5 8
#>
#> , , Sex = Female
#>
#> Eye
#> Hair Brown Blue Hazel Green
#> Black 36 9 5 2
#> Brown 66 34 29 14
#> Red 16 7 7 7
#> Blond 4 64 5 8
m_init <- dmod(~.^., data=HairEyeColor)Primero construye un modelo no dirigido que incluya todos los datos.
Vimos en una tarea anterior que la única indicación de dependencia entre aceptación y género estaba en un departamento particular (dept A). Construye entonces dos modelos log-lineales: uno para el departamento A y otro para el resto. Explica por qué usar dos modelos es mejor para uno solo para entender estos datos.