2.4 Estructura
Hasta ahora hemos considerado ajuste de modelos locales para estructuras gráficas ya dadas. Aunque en algunos casos la estructura de la red está dada por algún experto o restricciones naturales del fenómeno que nos interesa, también es común que tengamos que aprender la estructura a partir de los datos.
Vale la pena considerar los escenarios bajo los cuales se busca aprender una red.
Buscamos construir un modelo que nos permita responder queries probabilísticos generales (mismo objetivo que si elicito la red con conocimiento experto).
Buscamos predecir nuevas observaciones. Predecir variables objetivo \(y\) (vector) a partir de observaciones. Un ejemplo es en clasificación de imágenes o procesamiento de lenguaje.
No nos interesa una tarea de inferencia particular, sino descubrir conocimiento o estructura: distinguir entre dependencias directas e indirectas, posibles direccionalidades de los arcos.
Los objetivos anteriores se pueden satisfacer usando otras técnicas, algunas de las razones o situaciones por las que se utilizan modelos gráficos son: i) se busca predicción de objetos estructurados (explotar las correlaciones sobre varias variables), ii) se desea incorporar conocimiento experto al modelo, iii) tenemos un modelo unificado para múltiples variables, iv) es un marco para descubrir conocimiento.
Ahora, para aprender estructura existen dos tipos generales de algoritmos:
Aprendizaje basado en restricciones: algoritmos basados en pruebas de hipótesis de independencia entre variables. En este caso, el algoritmo se enfoca en explicar las relaciones de independencia y dependencia.
Aprendizaje basado en scores: estos algoritmos consideran las posibles estructuras gráficas como distintos modelos, de tal manera que el problema se convierte en uno de maximizar algún score que califica los distintos modelos. Es decir: definimos primero \(score({\mathcal G},p)\), donde \({\mathcal G}\) es una gráfica y \(p\) una distribución de probabilidad conjunta que se factoriza sobre \({\mathcal G}\), e intentamos resolver (o aproximar una solución) al problema
\[\max_{\mathcal G, p} score(\mathcal G,p)\]
En estas notas nos concentramos en aprendizaje basado en scores. Para esto, tendremos que definir una función apropiada de score, y una manera de aproximar la solución del problema de maximización mostrado arriba. Nuestro enfoque será heurístico, pues el problema de encontrar una solución exacta (máximo global) rápidamente se vuelve intratable conforme el número de nodos crece. Si tenemos \(k\) variables, y consideramos un solo ordenamiento \(X_1,\ldots, X_k\), entonces hay un total de \(2^1(2^2)\cdots (2^{k-1})=2^{k(k-1)/2}\) redes distintas que satisfacen el ordenamiento.
2.4.1 Scores de estructura
2.4.1.1 Máxima verosimilitud
Un posible score es la verosimilitud. Podríamos escoger un modelo, de entre todas las estructuras y parámetros posibles, usando máxima verosimilitud. Sin embargo, este enfoque no es apropiado para selección de modelos pues la verosimilitud siempre aumenta con la complejidad del modelo (aunque puede ser apropiado para estimar parámetros cuando la estructura es fija), y dado que el espacio de modelos con el que tratamos aquí generalmente es muy grande, es fácil sobreajustar los datos. Cuando sobreajustamos terminamos con modelos grandes, poco parsimoniosos y ruidosos que son difíciles de interpretar y que son malos en el pronóstico o la estimación de probabilidades condicionales.
Para entender esto recordemos máxima verosimilitud, supongamos que tenemos la muestra
\[{\mathcal L}= \{x^{(1)},x^{(2)}, \ldots, x^{(N)} \},\] donde cada \(x^{(i)}\) es una observación conjunta de las \(k\) variables \(X_1,X_2,\ldots, X_k\): \[x^{(i)}=(x^{(i)}_1,\ldots, x^{(i)}_k).\]
Ejemplo.
library(bnlearn)
library(plyr)
adm <- read.csv("data/admisiones.csv", stringsAsFactors = FALSE)
head(adm)
#> id Admit Gender Dept
#> 1 1 Admitted Male A
#> 2 2 Admitted Male A
#> 3 3 Admitted Male A
#> 4 4 Admitted Male A
#> 5 5 Admitted Male A
#> 6 6 Admitted Male A
adm_sub <- filter(adm, Dept %in% c("A", "B", "C"))En este ejemplo \(N=4,526\) y \(k=3\). Cada \(x^{(i)}\) es un renglón de la tabla.
Sea \({\mathcal G}\) una gráfica sobre los nodos \(X_1,\ldots, X_k\), y \(p\) una conjunta que se factoriza sobre \({\mathcal G}\). La verosimilitud de la red \(({\mathcal G}, p)\) es la probabilidad de observar los datos de entrenamiento \(\mathcal L\) dado el modelo \(({\mathcal G}, p),\) y la denotamos por \[L({\mathcal G}, p; {\mathcal L}).\]
Recordamos que si \(\mathcal L\) es una muestra, entonces \[L({\mathcal G}, p; {\mathcal L})=\prod_{i=1}^N p(x^{(i)}). \]
Entonces, buscamos maximizar esta verosimilitud sobre estructuras \({\mathcal G}\) junto con una conjunta \(p\) que se factoriza sobre \({\mathcal G}\), es decir resolver \[\max_{({\mathcal G}, p)} L({\mathcal G}, p; {\mathcal L})= \max_{\mathcal G} \max_{p\in M({\mathcal G})} \prod_{i=1}^N p(x^{(i)}) \]
Este problema es paramétrico, y podemos parametrizarlo usando los modelos locales que produce la factorización de \(p\) sobre \(\mathcal G\).
Ejemplo. Consideremos el modelo Gender -> Admit. Ambas variables tienen dos niveles, así que la conjunta se parametriza con 3 probabilidades. Como \(p\) se factoriza sobre la gráfica Gender -> Admit tenemos: \[p(Gender,Admit)=p(Gender)p(Admit|Gender),\] podemos parametrizar con \[\theta_1=p(Female), \theta_2=p(Admitted|Female), \theta_3=p(Admitted|Male),\] el resto de las probabilidades del modelo se calculan complementando estas tres.
Escribimos la verosimilitud haciendo explícitos los parámetros mediante
\[L( {\mathcal G},\theta_{\mathcal G};{\mathcal L} ),\]
donde \(\theta_{\mathcal G}\) representa los parámetros necesarios para obtener la conjunta \(p\) que se factorizan sobre la estructura \(\mathcal G\).
Con esta nueva notación, escribimos también:
\[L( {\mathcal G},\theta_{\mathcal G};{\mathcal L} )= \prod_{i=1}^N p(x^{(i)};\theta_{\mathcal G})\] donde $ p(x^{(i)};_{G})$ es la probabilidad conjunta de la observación \(x^{(i)}\) dados los parámetros \(\theta_{\mathcal G}\).
Ahora escribimos en términos de la factorización sobre \(\mathcal G\):
\[p(x^{(i)},\theta_{\mathcal G})=\prod_{j=1}^k p(x^{i}_j|x^{(i)};\theta_{\mathcal G}).\]
Y finalmente, observamos que en el \(j\)-ésimo factor \(p(x^{i}_j|x^{(i)};\theta_{\mathcal G})\), esta probabilidad sólo depende de las entradas de \(x^{(i)}\) que están en el conjunto de padres de \(X_j\), y además, que sólo depende de los parámetros en \(\theta_{\mathcal G}\) que se refieren a la parametrización del modelo local de \(X_j\).
Ejemplo En nuestro ejemplo anterior, tenemos que, para cualquier dato \(x^{(i)}=(a^{i}, g^{i})\), podríamos escribir \[p(a^{i};\theta_1)p(g^{i}|a^{i};\theta_2, \theta_3).\] El primer factor sólo depende de la primera coordenada \(a^{(i)}\) de \(x^{(i)}\) y del parámetro \(\theta_1\). El segundo factor depende de ambas coordenadas de \(x^{(i)}\) pero solamente de \(\theta_2, \theta_3.\)
Por lo tanto, la verosimilitud es:
\[L(Gender->Admit,(\theta_1,\theta_2,\theta_3);{\mathcal L})=\prod_{i=1}^N p(a^{i};\theta_1)p(g^{i}|a^{i};\theta_2, \theta_3),\]
Una vez que analizamos el ejemplo es fácil ver que tenemos el siguiente resultado:
La verosimilitud de una conjunta \(p\) que se factoriza sobre \(\mathcal G\) tiene una descomposición global en factores, donde en cada factor sólo intervienen los datos necesarios para los modelos locales y los parámetros correspondientes a cada modelo local.
Este resultado implica en particular que dada una gráfica \(\mathcal G\), la solución de máxima verosimilitud se puede calcular maximizando individualmente cada factor o modelo local, que es precisamente lo que explicamos en la clase anterior (usando tablas de frecuencias).
Usualmente trabajaremos con la log-verosimilitud, que está dada por \[loglik( {\mathcal G},\theta_{\mathcal G};{\mathcal L} )= \sum_{j=1}^k \sum_{i=1}^N \log p(x^{i}_j|x^{(i)};\theta_{\mathcal G}).\]
Muchas veces trabajamos también con la devianza, que es más útil para comparar modelos a lo largo de conjuntos de datos con distinto tamaño \(N\). La devianza se define como sigue:
\[Dev =-\frac{2}{N}loglik( {\mathcal G},\theta_{\mathcal G};{\mathcal L} )= -\frac{2}{N}\sum_{j=1}^k \sum_{i=1}^N \log p(x^{(i)},\theta_{\mathcal G})\]
Nótese que maximizar la verosimilitud es equivalente a maximizar la log-verosimilitud, y estas dos son equivalentes a minimizar la devianza.
Ejemplo. Si fijamos \(\mathcal G\) como la red con una sola arista que va de Gender a Admit, y dejamos sin aristas a Dept, tenemos que estimar 2 parámetros para la marginal de Dept, 1 parámetro para la marginal de Gender, y 2 parámetros para la condicional de Admit dado Gender. Así que \(\theta_G\) es un vector de longitud 5.
Podemos construir manualmente la función de verosimilitud como mostramos en el código de abajo. En este ejemplo, usamos una parametrización tipo logístico apropiada para minimizar la devianza sin restricciones. Por ejemplo, en lugar de parametrizar la como \((p_1,p_2)\to (p_1,p_2,1-p_1-p_2)\) la distribución sobre una variable que toma tres valores, usamos \[(\theta_1,\theta_2) \to \frac{1}{1+e^\theta_1+e^\theta_2}(e^\theta_1, e^\theta_2,1),\] y así los parámetros están libres.
logVerosimilitud <- function(datos) {
# logVerosimilitud recibe como parámetro los datos y devuelve la función
# de verosimilitud
function(theta){
p_1 <- exp(c(theta[1], 0)) / (1 + exp(theta[1]))
p_2 <- exp(c(theta[2], theta[3], 0)) / (1 + exp(theta[2]) + exp(theta[3]))
p_3 <- c(exp(c(theta[4], 0)) / (1 + exp(theta[4])), exp(c(theta[5], 0)) /
(1 + exp(theta[5])))
factor_1 <- data.frame(Gender = c('Male', 'Female'), prob_1 = p_1,
stringsAsFactors = FALSE)
factor_2 <- data.frame(Dept = c('A', 'B', 'C'), prob_2 = p_2,
stringsAsFactors = FALSE)
factor_3 <- data.frame(
Admit = c('Admitted', 'Rejected', 'Admitted', 'Rejected'),
Gender=c('Male', 'Male', 'Female', 'Female'), prob_3 = p_3,
stringsAsFactors = FALSE)
# producto cartesiano de los niveles
grid <- expand.grid(
Gender=c('Male','Female'),
Admit=c('Admitted','Rejected'),
Dept=c('A','B','C'), stringsAsFactors = FALSE) %>%
left_join(factor_1, by = "Gender") %>% # agregamos probabilidades
left_join(factor_2, by = 'Dept' ) %>%
left_join(factor_3, by = c('Admit', 'Gender'))
dat_p <- left_join(datos, grid, by = c('Gender', 'Dept', 'Admit'))
# log-verosimilitud
-sum(log(dat_p$prob_1) + log(dat_p$prob_2) + log(dat_p$prob_3))
}
}
logVer_1 <- logVerosimilitud(adm_sub)
class(logVer_1)
#> [1] "function"
logVer_1(rep(log(0.1), 5))
#> [1] 11318.47Si optimizamos numéricamente, obtenemos:
salida_1 <- optim(rep(0.1, 5), logVer_1)
(salida_1$par)
#> [1] 0.85675802 0.01824649 -0.45493261 0.30307326 -0.30528711
exp(salida_1$par[1]) / (1 + exp(salida_1$par[1]))
#> [1] 0.7019829
exp(salida_1$par[2]) / (1 + exp(salida_1$par[2]) + exp(salida_1$par[3]))
#> [1] 0.3838864
exp(salida_1$par[3]) / (1 + exp(salida_1$par[2]) + exp(salida_1$par[3]))
#> [1] 0.2391683
exp(salida_1$par[4]) / (1 + exp(salida_1$par[4]))
#> [1] 0.5751936
exp(salida_1$par[5]) / (1 + exp(salida_1$par[5]))
#> [1] 0.4242655Como habíamos explicado, estas probabilidades son precisamente las estimaciones que se obtienen de las tablas de frecuencias (máxima verosimilitud en cada factor):
prop.table(table(adm_sub$Gender))
#>
#> Female Male
#> 0.2980296 0.7019704
prop.table(table(adm_sub$Dept))
#>
#> A B C
#> 0.3830049 0.2401478 0.3768473
prop.table(table(adm_sub$Admit, adm_sub$Gender), 2)
#>
#> Female Male
#> Admitted 0.4242424 0.5760234
#> Rejected 0.5757576 0.4239766La verosimilitud alcanzada es
Repetimos el cálculo usando las función bn.fit de bnlearn con el fin de verificar que obtenemos el mismo resultado:
adm_sub_1 <- adm_sub %>%
dplyr::select(-id) %>%
mutate_each(funs(as.factor))
graf_adm_1 <- empty.graph(c('Admit','Gender','Dept'))
arcs(graf_adm_1) <- matrix(c('Gender', 'Admit'), ncol = 2)
fit_1 <- bn.fit(graf_adm_1, data = adm_sub_1)
fit_1
#>
#> Bayesian network parameters
#>
#> Parameters of node Admit (multinomial distribution)
#>
#> Conditional probability table:
#>
#> Gender
#> Admit Female Male
#> Admitted 0.4242424 0.5760234
#> Rejected 0.5757576 0.4239766
#>
#> Parameters of node Gender (multinomial distribution)
#>
#> Conditional probability table:
#> Female Male
#> 0.2980296 0.7019704
#>
#> Parameters of node Dept (multinomial distribution)
#>
#> Conditional probability table:
#> A B C
#> 0.3830049 0.2401478 0.3768473
logLik(fit_1, data = adm_sub_1)
#> [1] -5770.0742.4.1.2 Máxima verosimilitud y sobreajuste
En muchos casos, utilizar máxima verosimilitud para estimar modelos complejos con datos relativamente ralos es mala idea, debido a que al intentar maximizar el ajuste podemos acabar ajustando ruido como si fuera estructura. Veamos que pasa si evaluamos distintas estructuras en nuestro ejemplo de admisiones:
set.seed(6391572)
adm_f <- adm %>%
mutate_each(funs(factor), Admit, Gender, Dept)
# datos de entrenamiento
adm_ent <- sample_n(adm_f, 300)
#datos de validación
adm_val <- anti_join(adm_f, adm_ent, by = "id")Comparamos 3 modelos:
modelo_0 <- empty.graph(c('Gender', 'Dept', 'Admit'))
modelo_1 <- modelo_0
arcs(modelo_1) <- matrix(c('Gender', 'Dept'), ncol = 2, byrow = T)
modelo_2 <- modelo_0
arcs(modelo_2) <- matrix(c('Gender', 'Dept', 'Dept', 'Admit'), ncol = 2,
byrow = T)
modelo_3 <- modelo_0
arcs(modelo_3) <- matrix(c('Gender', 'Dept', 'Dept', 'Admit', 'Gender',
'Admit'), ncol = 2, byrow = T)El modelo más sencillo corresponde a independencia,
fit_0 <- bn.fit(modelo_0, data = adm_ent)
devianza_0 <- -2 * logLik(fit_0, data = adm_ent) / nrow(adm_ent)
devianza_0
#> [1] 6.236199Ahora consideramos un arco de Gender a Dept, notamos que se reduce la devianza:
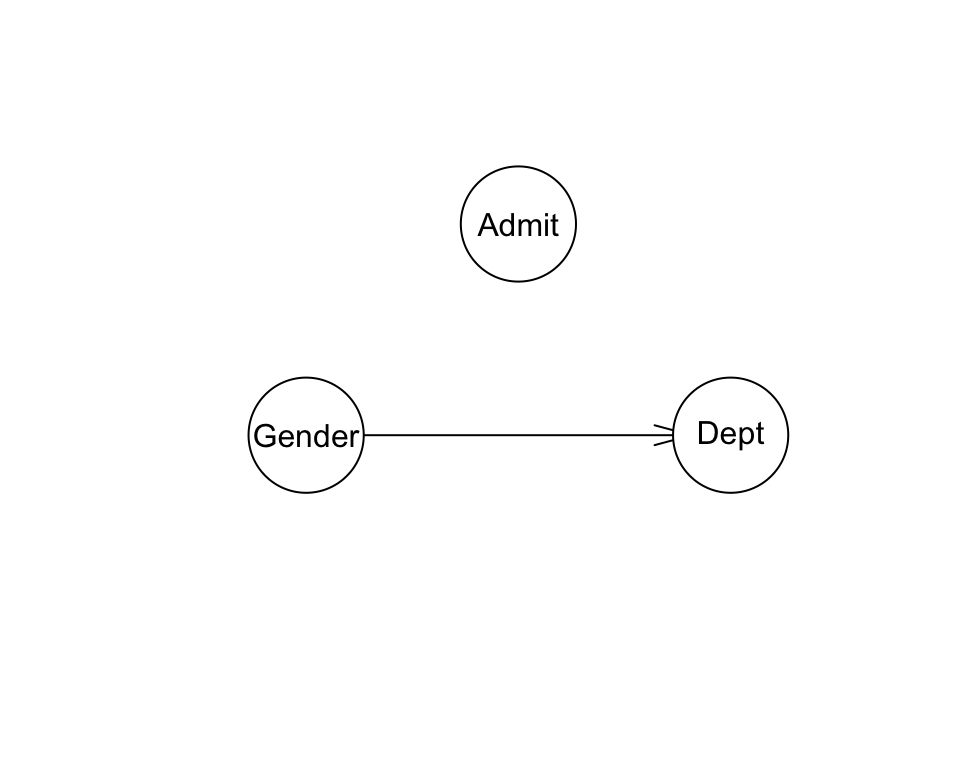
fit_1 <- bn.fit(modelo_1, data = adm_ent)
devianza_1 <- -2 * logLik(fit_1, data = adm_ent) / nrow(adm_ent)
devianza_1
#> [1] 5.986321Agregamos un arco de Dept a Admit,
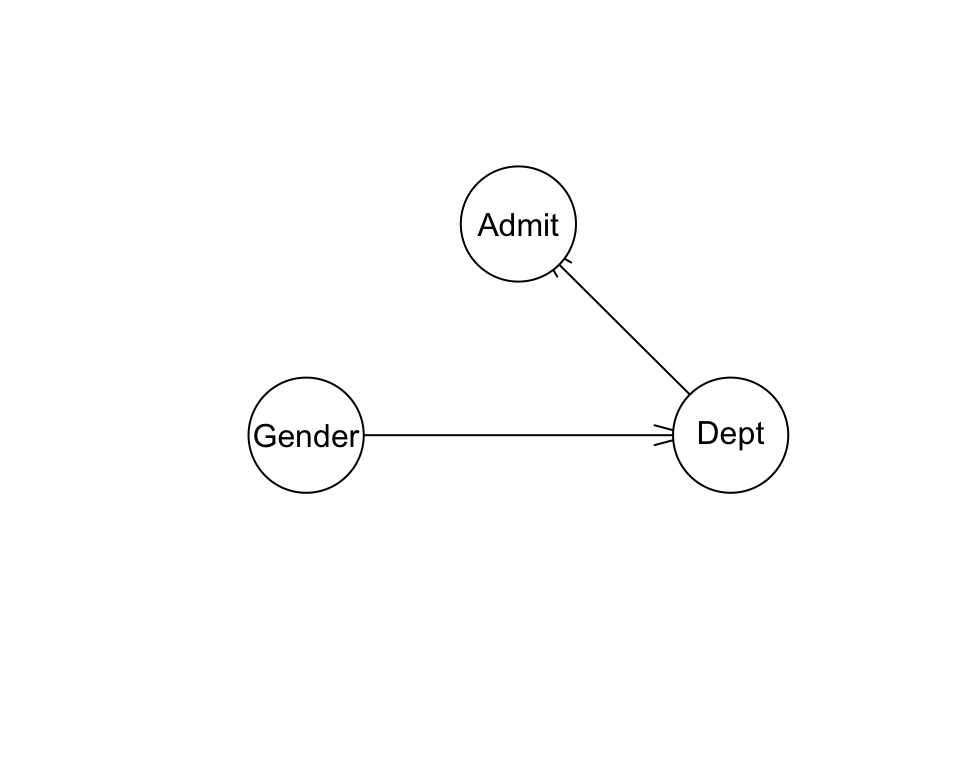
fit_2 <- bn.fit(modelo_2, data = adm_ent)
devianza_2 <- -2 * logLik(fit_2, data = adm_ent) / nrow(adm_ent)
devianza_2
#> [1] 5.833935Y finalmente agregamos un arco más de Gender a Admit:
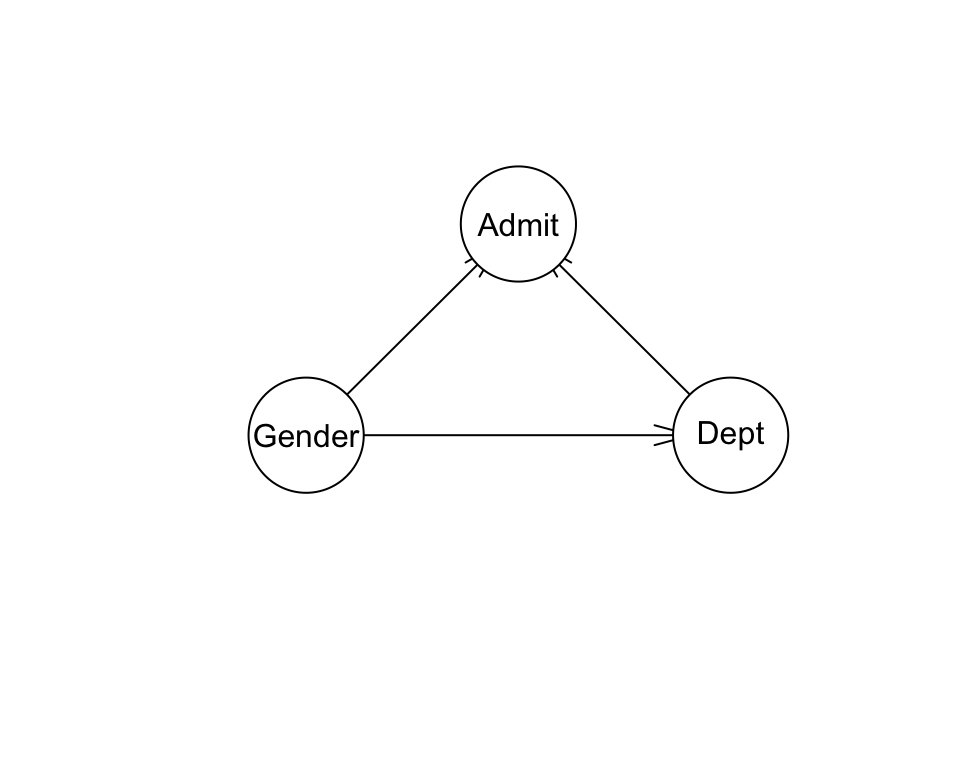
fit_3 <- bn.fit(modelo_3, data = adm_ent)
devianza_3 <- -2 * logLik(fit_3, data = adm_ent) / nrow(adm_ent)
devianza_3
#> [1] 5.808581En todos estos casos, la devianza se redujo, como esperábamos. Sin embargo, ¿qué pasa si observamos un nuevo conjunto de datos generado por el mismo fenómeno? ¿Cuál se desempeño de cada modelo, ¿Cuál explica mejor los nuevos datos? Calcularemos entonces la devianza con una muestra de validación, esta es una muestra independiente de la que se usó para ajustar los modelos.
library(tidyr)
library(ggplot2)
adm_val <- dplyr::select(adm_val, -id)
modelos <- list(fit_0, fit_1, fit_2, fit_3)
resultados <- ldply(1:4, function(i){
data.frame(modelo = i,
dev_ent = -2 * logLik(modelos[[i]], data = adm_ent) / nrow(adm_ent),
dev_val = -2 * logLik(modelos[[i]], data = adm_val) / nrow(adm_val))
})
res_m <- gather(resultados, muestra, devianza, dev_ent:dev_val)
ggplot(res_m, aes(x = modelo, y = devianza, colour = muestra, group = muestra)) +
geom_point() +
geom_line()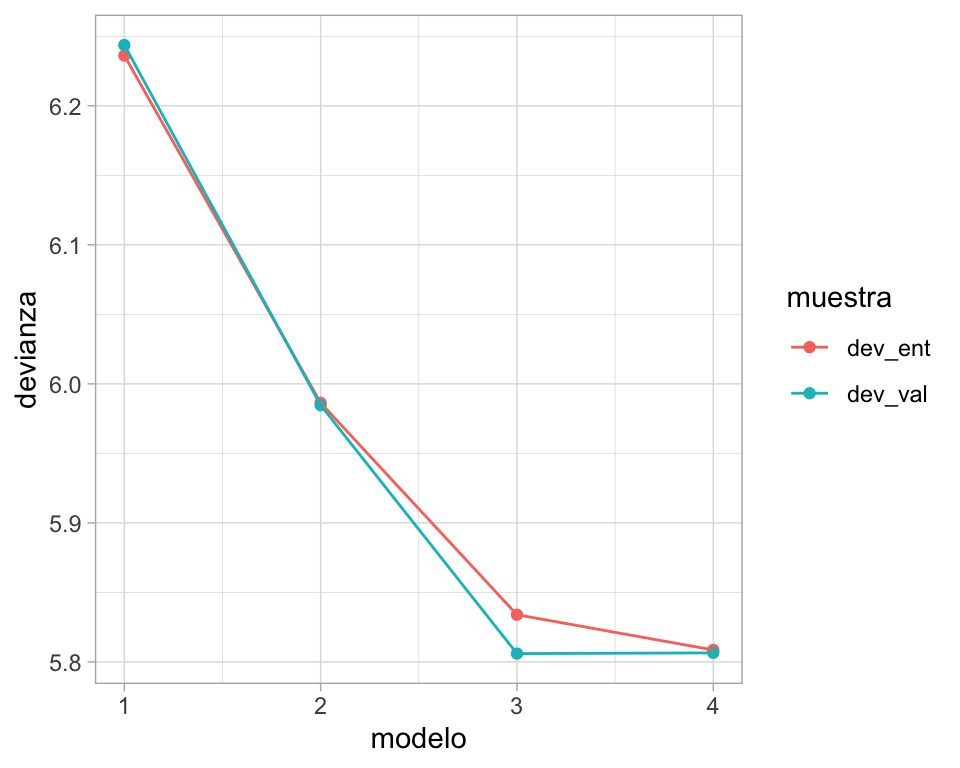
Al evaluar con una nueva muestra, vemos entonces que el modelo de tres arcos se desempeña peor o de manera similarque el modelo más simple con dos aristas. Esto sugiere que el modelo más parsimonioso es superior al que tiene tres aristas.
El problema es que máxima verosimilitud siempre califica mejor a los modelos más complejos pues el ajuste a los datos de entrenamiento siempre es mejor con modelos más complejos. Sin embargo, la muestra de validación sugiere que esta ganancia en ajuste sólo es cierta para la muestra de entrenamiento, y no es replicable para otras muestras del mismo fenómeno. A su vez, esto indica que esa mejora en ajuste se debe a que el modelo más complejo mejoró porque está explicando variación muestral, o características de la muestra particular que usamos para entrenar. Pero estos resultados no son generalizables o replicables.
Es posible seleccionar modelos usando muestras de validación (y es un enfoque muy robusto desde el punto de vista teórico), como hicimos arriba. Sin embargo, cuando no tenemos muchos datos, el modelo seleccionado puede ser uno relativamente malo en comparación a lo que obtendríamos con toda la muestra. En realidad no estamos desaprovechando datos (unos se usan para estimar parámetros y otros para seleccionar modelos), pero en casos donde hay muchas variables preferiremos hacer aproximaciones, en lugar de usar muestras de validación, para seleccionar modelos ajustados con la totalidad de los datos.
2.4.1.3 Penalización por complejidad y score AIC
Una solución al problema de selección de modelos es cambiar la función de score por una que penalice la verosimilitud según el número de parámetros en el modelo. Una medida popular de este es el AIC (Aikaike information criterion). El AIC se define como
El score AIC de un modelo se define como \[AIC({\mathcal G}, \theta_{\mathcal G}) = -\frac{2}{N}loglik + \frac{2d}{N}=Dev + \frac{2d}{N},\] donde \(d\) es el número de parámetros en \(\theta_{\mathcal G}.\)
Nótemos que bajo este score, agregar una arista no necesariamente representa una mejora, pues aunque \(loglik\) no aumenta o disminuye, \(d\) definitivamente aumenta (añadimos variables en los modelos locales). Es decir, el AIC es una combinación de una medida de ajuste del modelo con una penalización por complejidad, donde medimos complejidad por el número de parámetros del modelo.
El score AIC es una aproximación asintótica (\(N\) grande) al valor esperado de la devianza sobre datos de prueba, independientes de la muestra de entrenamiento o ajuste que utilizamos. Tiene sentido intentar minimizar este valor esperado: esto indica buen desempeño para observaciones fuera de nuestra muestra, que es en realidad lo que queremos lograr, e ignorar mejoras que sólo se deben a particularidades de nuestra muestra de entrenamiento.
En el ejmplo de admisiones podemos ver que,
loglike_2 <- logLik(modelos[[2]], data = adm_ent)
aic_2 <- AIC(modelos[[2]], data = adm_ent)
loglike_2
#> [1] -897.9482
aic_2
#> [1] -909.9482
loglike_2 - aic_2
#> [1] 12Efectivamente, el modelo 2 tiene 12 parámetros:
modelos[[2]]
#>
#> Bayesian network parameters
#>
#> Parameters of node Gender (multinomial distribution)
#>
#> Conditional probability table:
#> Female Male
#> 0.43 0.57
#>
#> Parameters of node Dept (multinomial distribution)
#>
#> Conditional probability table:
#>
#> Gender
#> Dept Female Male
#> A 0.077519380 0.292397661
#> B 0.007751938 0.216374269
#> C 0.294573643 0.116959064
#> D 0.248062016 0.175438596
#> E 0.170542636 0.081871345
#> F 0.201550388 0.116959064
#>
#> Parameters of node Admit (multinomial distribution)
#>
#> Conditional probability table:
#> Admitted Rejected
#> 0.3833333 0.6166667¿Qué modelo debemos elegir de acuerdo al AIC?
resultados <- ldply(1:4, function(i){
data.frame(modelo = i,
dev_ent = -2 * logLik(modelos[[i]], data = adm_ent) / nrow(adm_ent),
dev_val = -2 * logLik(modelos[[i]], data = adm_val) / nrow(adm_val),
aic = -2 * AIC(modelos[[i]], data = adm_val) / nrow(adm_val))
})
res_m <- gather(resultados, muestra, devianza, dev_ent:aic)
ggplot(res_m, aes(x = modelo, y = devianza, colour = muestra, group = muestra)) +
geom_point() +
geom_line()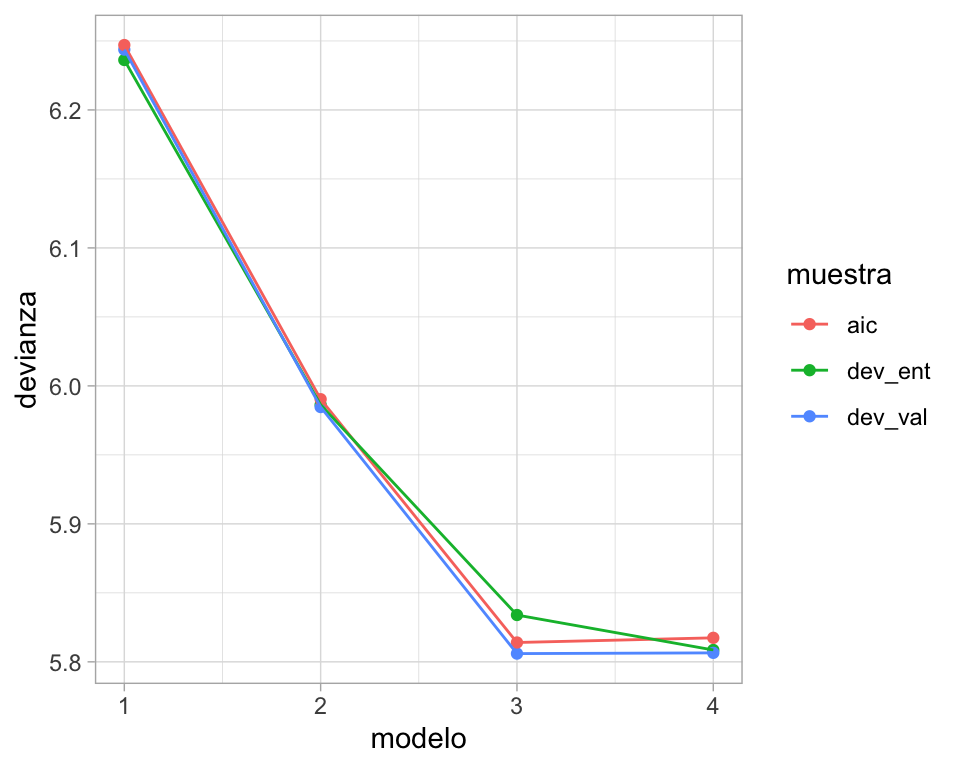
No hay garantía de escoger el modelo óptimo usando el AIC (según la experiencia tiende a escoger modelos quizá demasiado complejos), pero es una guía útil para controlar complejidad.
Otra alternativa útil es el BIC, que también es un tipo de verosimilitud penalizada:
Hay otros scores que se utilizan. Un ejemplo es el BIC (Bayesian Information Criterion), que en lugar de penalizar por \(d\), penaliza por \(\frac{\log(N)}{2}d\). Este criterio resulta en modelos más simples (ver referencia de Koller, 18.3.2).
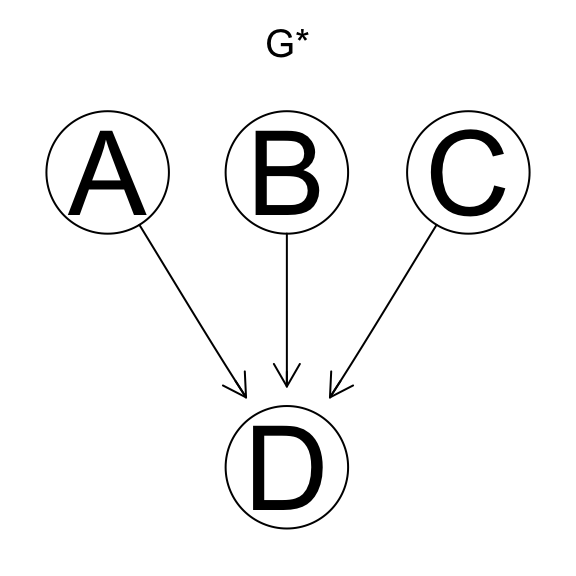
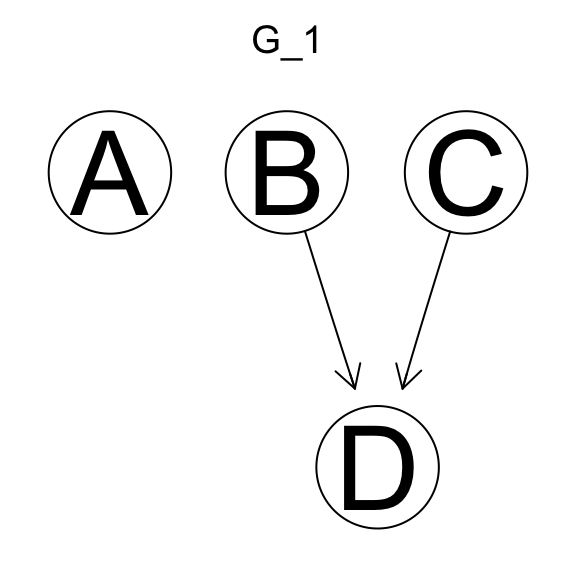
Considera \(\mathcal G^*\) la verdadera red y \(\mathcal G_1\), \(\mathcal G_2\) redes aprendidas. Definamos \(p*\) tal que \(\mathcal G^*\) es un mapeo perfecto de \(\mathcal G*\) (\(I(\mathcal G^*)=I(p^*)\)) Entonces,
- \(\mathcal G_1\) y \(\mathcal G_2\) se pueden usar para aprender \(\mathcal p^*\)
de manera correcta.
- \(\mathcal G_1\) se puede usar para aprender \(p^*\) de manera correcta
pero \(\mathcal G_2\) no.
- \(\mathcal G_2\) se puede usar para aprender \(p^*\) de manera correcta
pero \(\mathcal G_1\) no.
- Ninguna se puede usar para aprender \(p^*\) de manera correcta.
En la práctica se utilizan AIC y BIC. El AIC tiende a producir modelos más complejos con algún sobreajuste, mientras que el BIC tiende a producir modelos más simples y a veces con falta de ajuste. No hay acuerdo en qué medida es mejor en general, pero el balance se puede considerar como sigue: cuando es importante predecir o hacer inferencia, y no nos preocupa tanto obtener algunas aristas espurias, preferimos el AIC. Cuando buscamos la parte más robusta de la estructura de variación de las variables, aún cuando perdamos algunas dependencias débiles, puede ser mejor usar el BIC.
2.4.2 Procedimiento de búsqueda
Nuestro siguiente paso es describir la heurística de búsqueda para minimizar el score, que en lo que sigue suponemos que es el AIC.
Hay dos decisiones de diseño para decidir el algoritmo de aprendizaje de estructura:
Técnicas de busqueda.
* Hill-climbing
* Recocido simulado
* Algoritmos genéticos
Operadores de búsqueda
Locales
* Agregar arista
* Eliminar arista
* Cambiar dirección de arista
Globales (ej. cambiar un nodo de lugar, más costoso)
Aunque hay varios algoritmos, uno utilizado comunmente es el de hill climbing.
2.4.3 Hill-climbing
- Iniciamos con una gráfica dada:
- Gráfica vacía
- Gráfica aleatoria
- Conocimiento experto
- En cada iteración:
- Consideramos el score para cada operador de búsqueda local (agregar, eliminar o cambiar la dirección de una arista)
- Aplicamos el cambio que resulta en un mayor incremento en el score. Si tenemos empates elijo una operación al azar.
- Parar cuando ningún cambio resulte en mejoras del score.
Ejemplo. Eliminación de aristas Consideremos datos simulados de una red en forma de diamante:
set.seed(28)
n <- 600 # número de observaciones
a <- (rbinom(n, 1, 0.3)) # nodo raíz
b <- (rbinom(n, 1, a * 0.1 + (1 - a) * 0.8))
c <- (rbinom(n, 1, a * 0.2 + (1 - a) * 0.9))
d <- (rbinom(n, 1, b * c * 0.9 + (1 - b * c) * 0.1))
dat <- data.frame(a = factor(a), b = factor(b), c = factor(c), d = factor(d))
head(dat)
#> a b c d
#> 1 0 1 1 1
#> 2 0 1 1 1
#> 3 0 1 1 1
#> 4 1 0 0 0
#> 5 0 1 1 1
#> 6 1 0 0 0Y supongamos que comenzamos el proceso con una gráfica vacía:
aic <- function(fit, data){
-2 * AIC(fit, data = data) / nrow(data)
}
grafica_0 <- empty.graph(c('a','b','c','d'))
fit_0 <- bn.fit(grafica_0, dat)
logLik(fit_0, data = dat)
#> [1] -1543.696
AIC(fit_0, data = dat) # cuatro parámetros
#> [1] -1547.696
aic(fit_0, data = dat)
#> [1] 5.158988Consideramos agregar \(a\to d\), la nueva arista que mejora el AIC, y escogemos este cambio. Notemos que esta arista no existe en el modelo que genera los datos,
grafica_1 <- grafica_0
arcs(grafica_1) <- matrix(c('a', 'd'), ncol = 2, byrow = T)
fit_1 <- bn.fit(grafica_1, dat)
logLik(fit_1, data = dat)
#> [1] -1458.222
aic(fit_1, data = dat)
#> [1] 4.877407
graphviz.plot(grafica_1)
Ahora agregamos \(a\to b\), que también mejora el AIC:
grafica_2 <- grafica_0
arcs(grafica_2) <- matrix(c('a','d','a','b'), ncol = 2, byrow = T)
fit_2 <- bn.fit(grafica_2, dat)
logLik(fit_2, data = dat)
#> [1] -1288.1
aic(fit_2, data = dat)
#> [1] 4.313667
graphviz.plot(grafica_2)
Igualmente, agregar \(a\to c\) merjoar el AIC:
grafica_3 <- grafica_0
arcs(grafica_3) <- matrix(c('a','d','a','b','a','c'), ncol = 2, byrow = T)
fit_3 <- bn.fit(grafica_3, dat)
logLik(fit_3, data = dat )
#> [1] -1141.835
aic(fit_3, data = dat)
#> [1] 3.829451
graphviz.plot(grafica_3)
Agregamos \(b\to d\) y \(c\to d\):
grafica_4 <- grafica_0
arcs(grafica_4) <- matrix(c('a','d','a','b','a','c','b','d'), ncol = 2,
byrow = T)
fit_4 <- bn.fit(grafica_4, dat)
logLik(fit_4, data = dat )
#> [1] -1064.735
aic(fit_4, data = dat)
#> [1] 3.579116
grafica_4 <- grafica_0
arcs(grafica_4) <- matrix(c('a','d','a','b','a','c','b','d','c','d'), ncol = 2,
byrow = T)
fit_4 <- bn.fit(grafica_4, dat)
logLik(fit_4, data = dat )
#> [1] -1015.777
aic(fit_4, data = dat)
#> [1] 3.429258
graphviz.plot(grafica_4)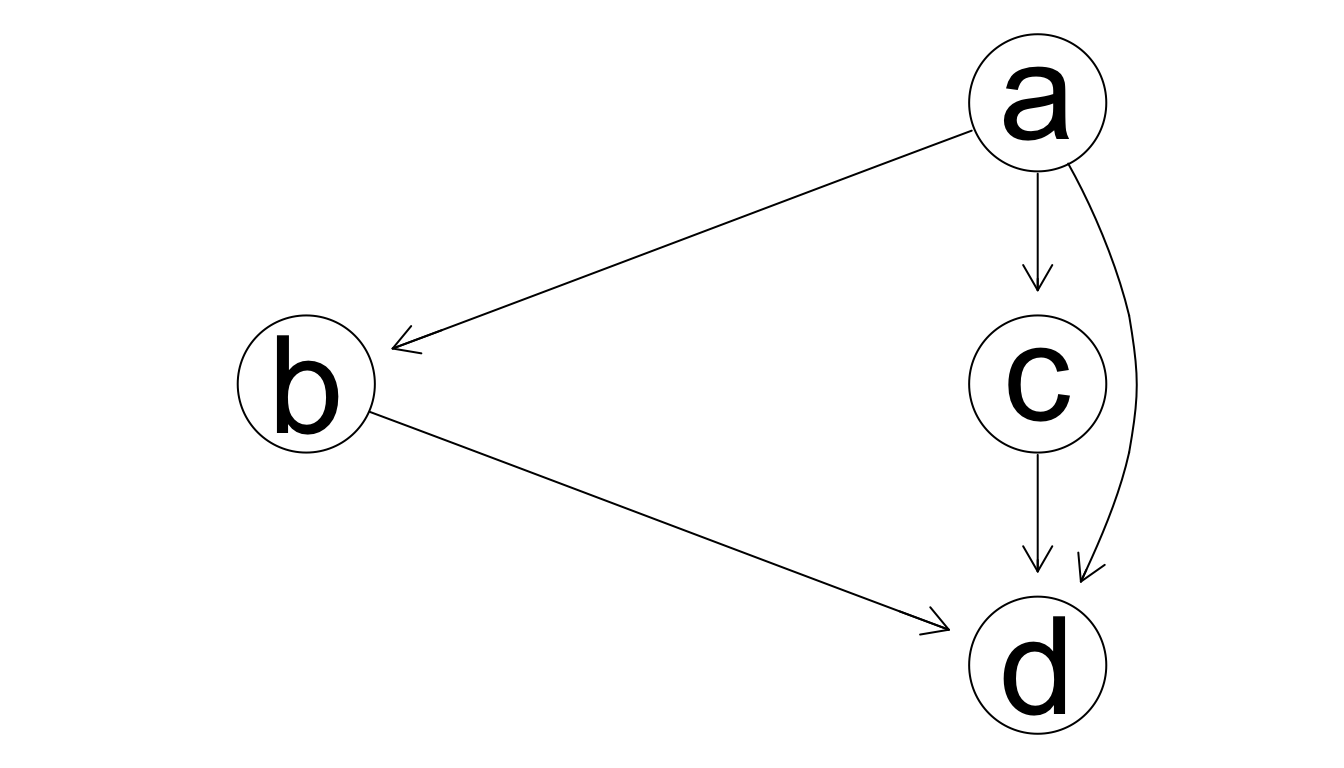
Ahora nótese que podemos eliminar \(a\to d\), y mejoramos el AIC:
grafica_5 <- grafica_0
arcs(grafica_5) <- matrix(c('a','b','a','c','b','d','c','d'), ncol = 2,
byrow = T)
fit_5 <- bn.fit(grafica_5, dat)
logLik(fit_5, data = dat )
#> [1] -1016.166
aic(fit_5, data = dat)
#> [1] 3.417219
graphviz.plot(grafica_5)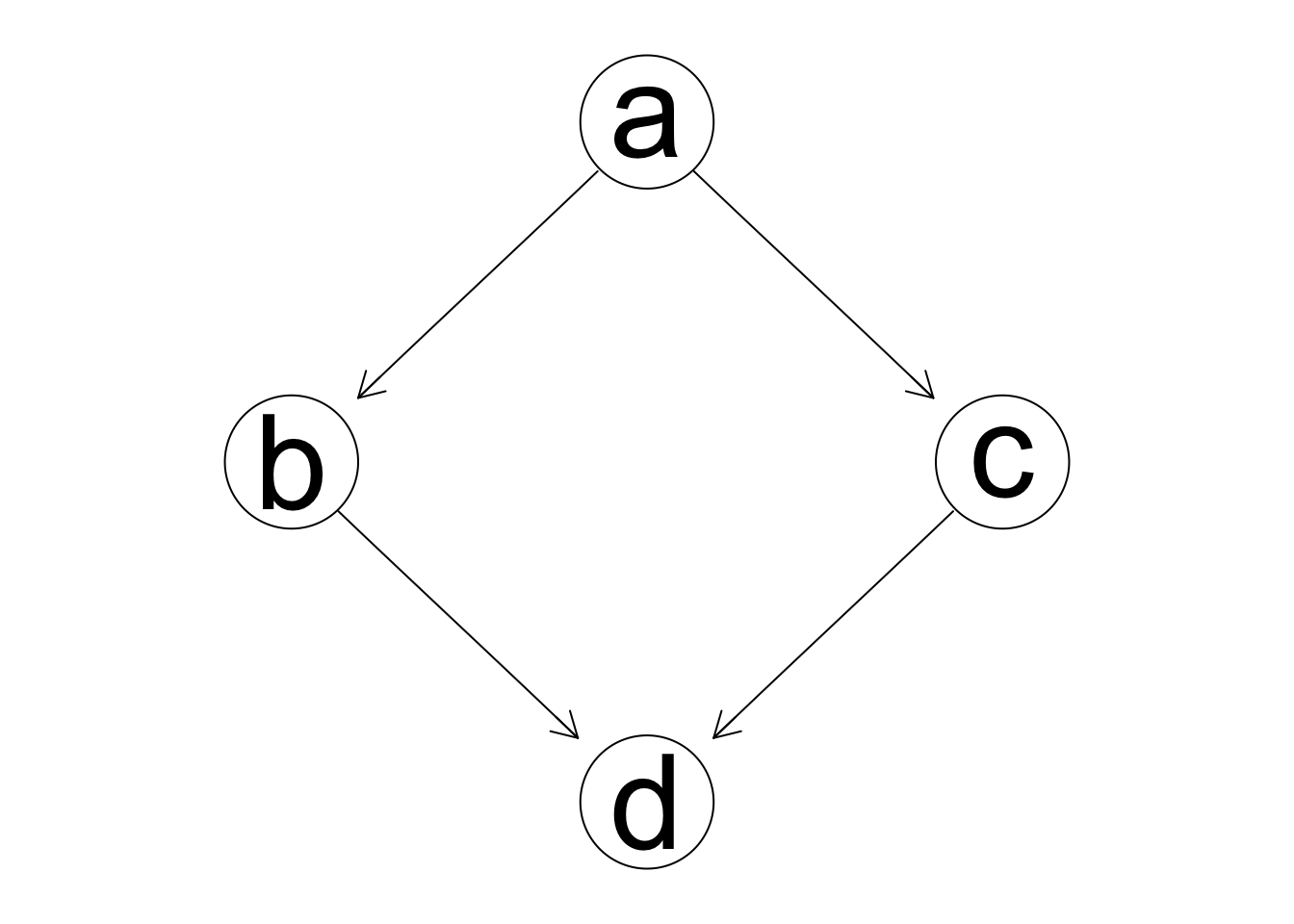
Este última gráfica es el modelo original. La eliminación de arcos nos permitió recuperar el modelo original a pesar de nuestra decisión inicial temporalmente incorrecta de agregar \(a\to d\).
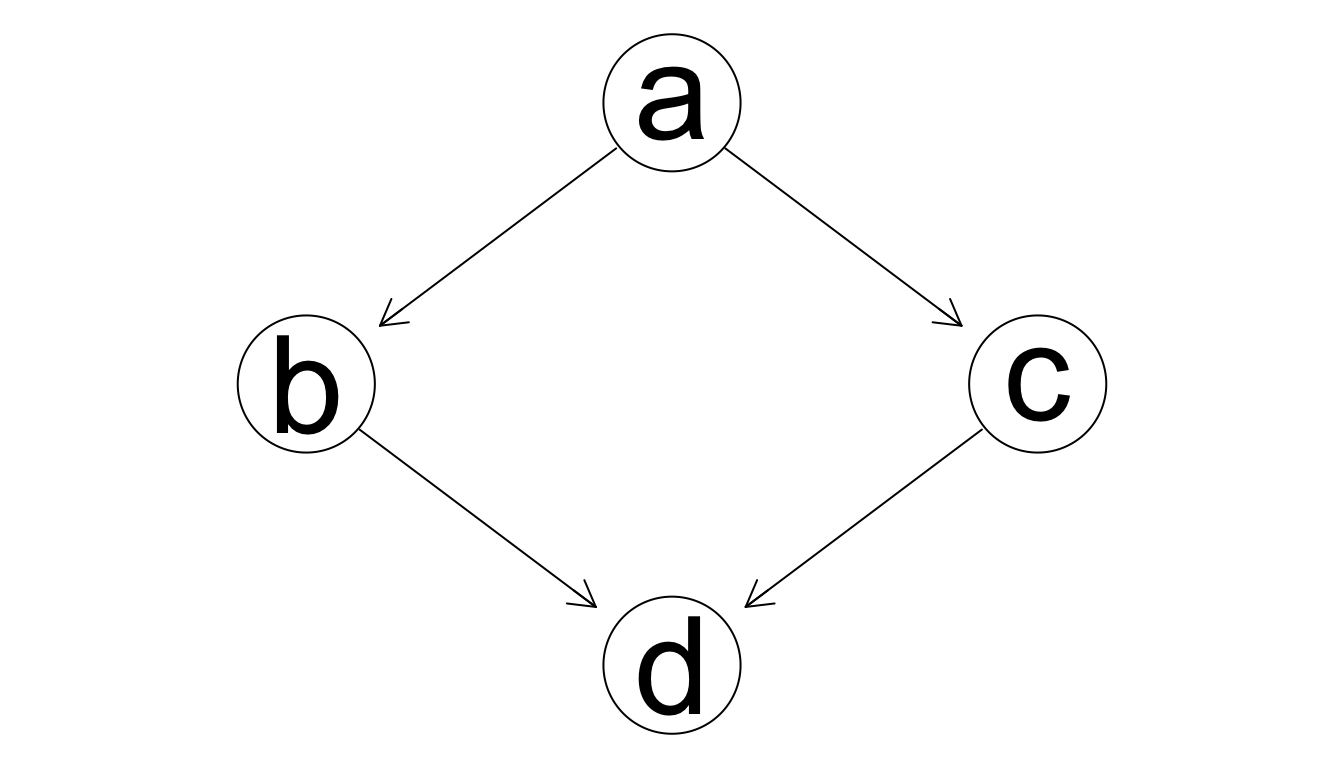
El algoritmo de hill climbing como está implementado en bn.learn resulta en:
Ejemplo: Cambios de dirección
Consideramos un ejemplo simple con un colisionador:
set.seed(28)
n <- 600
b <- (rbinom(n, 1, 0.4))
c <- (rbinom(n, 1, 0.7))
d <- (rbinom(n, 1, b*c*0.9+ (1-b*c)*0.1 ))
dat <- data.frame(factor(b),factor(c),factor(d))
names(dat) <- c('b','c','d')Supongamos que comenzamos agregando la arista \(d\to c\) (sentido incorrecto).
grafica_0 <- empty.graph(c('b','c','d'))
arcs(grafica_0) <- matrix(c('d','c'), ncol=2, byrow=T)
graphviz.plot(grafica_0)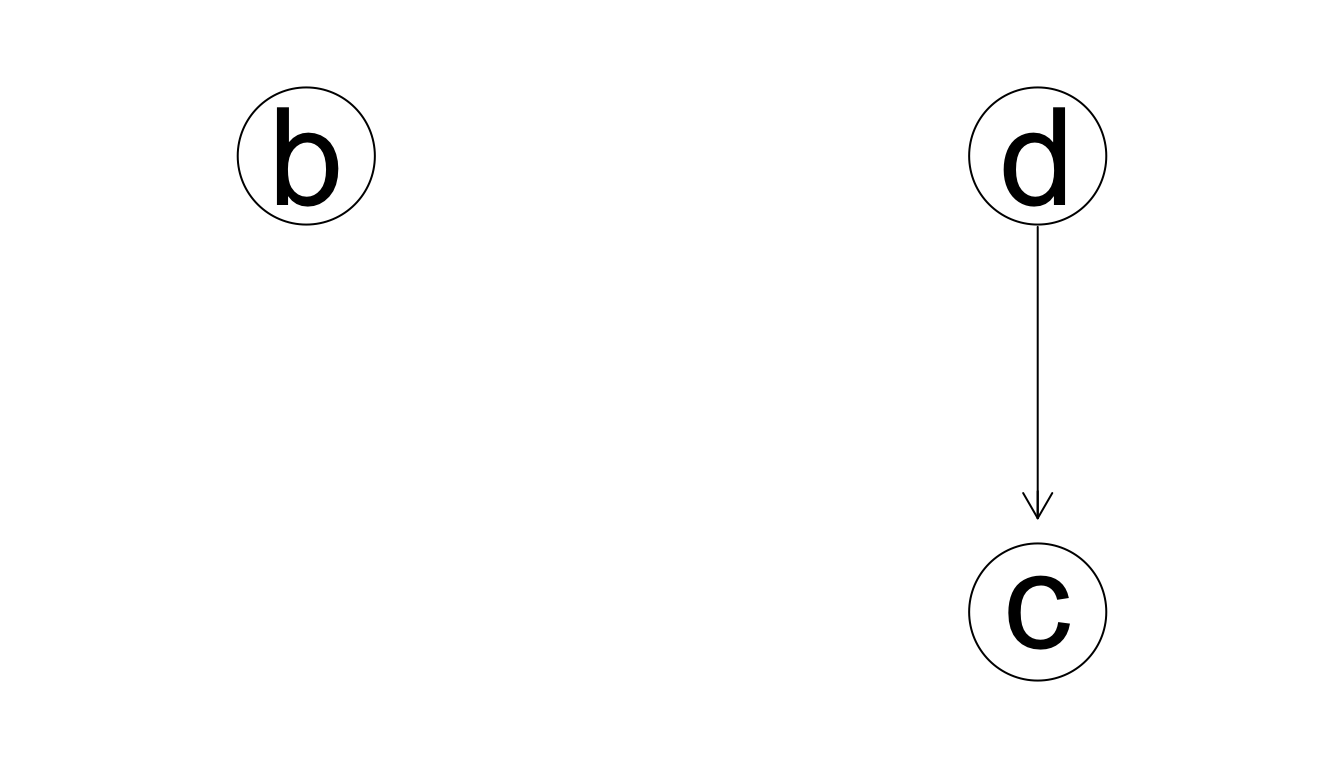
En el primer paso, agregamos \(b \to d\), que muestra una mejora grande:
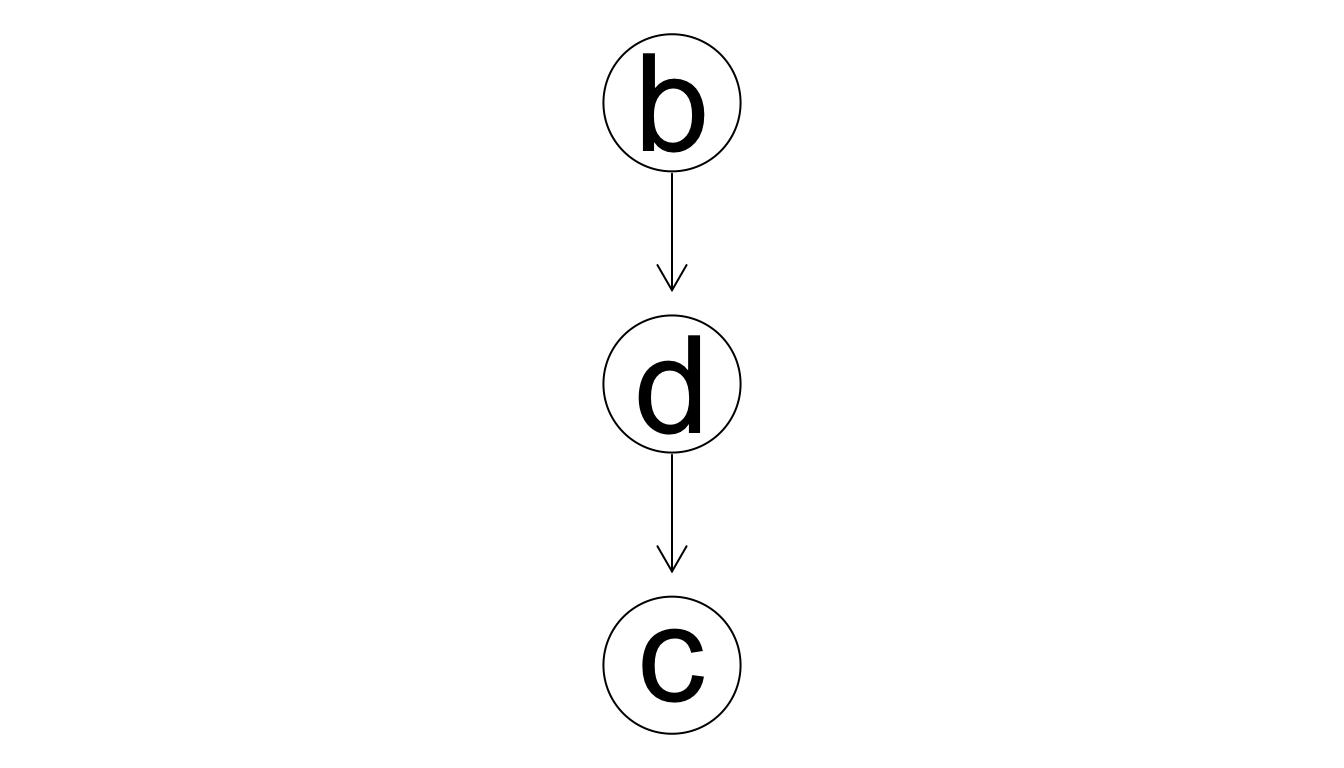
Pero en el siguiente paso nos damos cuenta que podemos mejorar considerablemente si construimos el modelo local de \(d\) a partir no sólo de \(b\) sino también de \(c\), y cambiamos dirección:
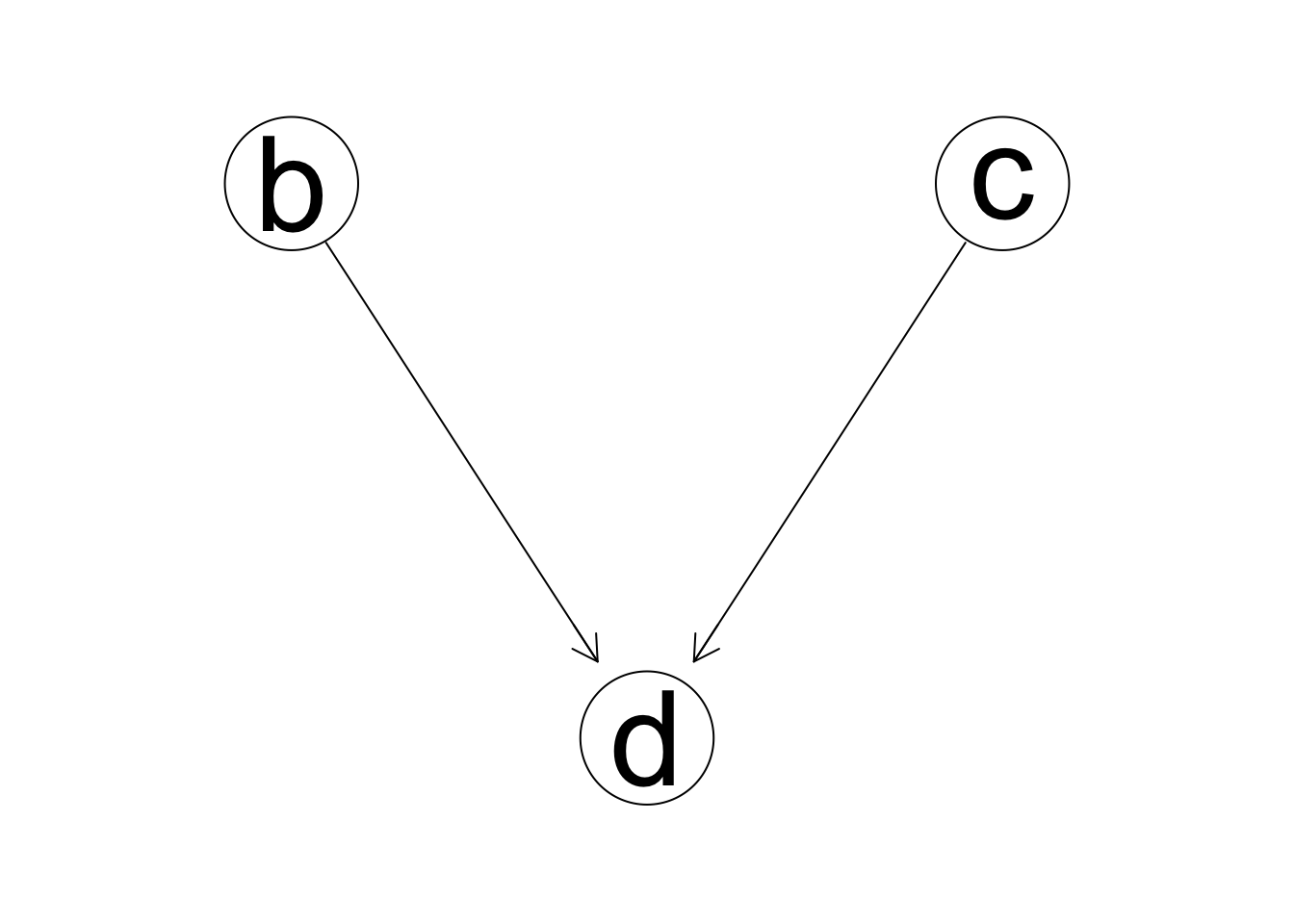
Podemos examinar cada paso del algoritmo:
hc(dat, start = grafica_0, score='aic', debug=T)
#> ----------------------------------------------------------------
#> * starting from the following network:
#>
#> Random/Generated Bayesian network
#>
#> model:
#> [b][d][c|d]
#> nodes: 3
#> arcs: 1
#> undirected arcs: 0
#> directed arcs: 1
#> average markov blanket size: 0.67
#> average neighbourhood size: 0.67
#> average branching factor: 0.33
#>
#> generation algorithm: Empty
#>
#> * current score: -1105.878
#> * whitelisted arcs are:
#> * blacklisted arcs are:
#> * caching score delta for arc b -> c (51.958371).
#> * caching score delta for arc b -> d (127.579833).
#> * caching score delta for arc c -> b (-0.955426).
#> * caching score delta for arc c -> d (25.648932).
#> * caching score delta for arc d -> c (-25.648932).
#> ----------------------------------------------------------------
#> * trying to add one of 4 arcs.
#> > trying to add b -> c.
#> > delta between scores for nodes b c is 51.958371.
#> @ adding b -> c.
#> > trying to add b -> d.
#> > delta between scores for nodes b d is 127.579833.
#> @ adding b -> d.
#> > trying to add c -> b.
#> > delta between scores for nodes c b is -0.955426.
#> > trying to add d -> b.
#> > delta between scores for nodes d b is 127.579833.
#> ----------------------------------------------------------------
#> * trying to remove one of 1 arcs.
#> > trying to remove d -> c.
#> > delta between scores for nodes d c is -25.648932.
#> ----------------------------------------------------------------
#> * trying to reverse one of 1 arcs.
#> > trying to reverse d -> c.
#> > delta between scores for nodes d c is 0.000000.
#> ----------------------------------------------------------------
#> * best operation was: adding b -> d .
#> * current network is :
#>
#> Bayesian network learned via Score-based methods
#>
#> model:
#> [b][d|b][c|d]
#> nodes: 3
#> arcs: 2
#> undirected arcs: 0
#> directed arcs: 2
#> average markov blanket size: 1.33
#> average neighbourhood size: 1.33
#> average branching factor: 0.67
#>
#> learning algorithm: Hill-Climbing
#> score: AIC (disc.)
#> penalization coefficient: 1
#> tests used in the learning procedure: 5
#> optimized: TRUE
#>
#> * current score: -978.2983
#> * caching score delta for arc b -> d (-127.579833).
#> * caching score delta for arc c -> d (78.562729).
#> ----------------------------------------------------------------
#> * trying to add one of 2 arcs.
#> > trying to add b -> c.
#> > delta between scores for nodes b c is 51.958371.
#> @ adding b -> c.
#> > trying to add c -> b.
#> > delta between scores for nodes c b is -0.955426.
#> ----------------------------------------------------------------
#> * trying to remove one of 2 arcs.
#> > trying to remove b -> d.
#> > delta between scores for nodes b d is -127.579833.
#> > trying to remove d -> c.
#> > delta between scores for nodes d c is -25.648932.
#> ----------------------------------------------------------------
#> * trying to reverse one of 2 arcs.
#> > trying to reverse b -> d.
#> > delta between scores for nodes b d is 0.000000.
#> > trying to reverse d -> c.
#> > delta between scores for nodes d c is 52.913797.
#> @ reversing d -> c.
#> ----------------------------------------------------------------
#> * best operation was: reversing d -> c .
#> * current network is :
#>
#> Bayesian network learned via Score-based methods
#>
#> model:
#> [b][c][d|b:c]
#> nodes: 3
#> arcs: 2
#> undirected arcs: 0
#> directed arcs: 2
#> average markov blanket size: 2.00
#> average neighbourhood size: 1.33
#> average branching factor: 0.67
#>
#> learning algorithm: Hill-Climbing
#> score: AIC (disc.)
#> penalization coefficient: 1
#> tests used in the learning procedure: 7
#> optimized: TRUE
#>
#> * current score: -925.3845
#> * caching score delta for arc b -> c (-0.955426).
#> * caching score delta for arc b -> d (-180.493630).
#> * caching score delta for arc c -> d (-78.562729).
#> * caching score delta for arc d -> c (25.648932).
#> ----------------------------------------------------------------
#> * trying to add one of 2 arcs.
#> > trying to add b -> c.
#> > delta between scores for nodes b c is -0.955426.
#> > trying to add c -> b.
#> > delta between scores for nodes c b is -0.955426.
#> ----------------------------------------------------------------
#> * trying to remove one of 2 arcs.
#> > trying to remove b -> d.
#> > delta between scores for nodes b d is -180.493630.
#> > trying to remove c -> d.
#> > delta between scores for nodes c d is -78.562729.
#> ----------------------------------------------------------------
#> * trying to reverse one of 2 arcs.
#> > trying to reverse b -> d.
#> > delta between scores for nodes b d is -52.913797.
#> > trying to reverse c -> d.
#> > delta between scores for nodes c d is -52.913797.Ejemplo simulado.
Comenzamos con una muestra relativamente chica, y utilizamos el BIC:
set.seed(280572)
n <- 300
a <- (rbinom(n, 1, 0.2))
b <- (rbinom(n, 1, a*0.1+(1-a)*0.8))
c <- (rbinom(n, 1, a*0.2+(1-a)*0.9))
d <- (rbinom(n, 1, b*c*0.9+ (1-b*c)*0.1 ))
e <- rbinom(n, 1, 0.4)
f <- rbinom(n, 1, e*0.3+(1-e)*0.6)
g <- rbinom(n, 1, f*0.2+(1-f)*0.8)
dat <- data.frame(factor(a),factor(b),factor(c),factor(d), factor(e), factor(f),
factor(g))
names(dat) <- c('a','b','c','d','e','f','g')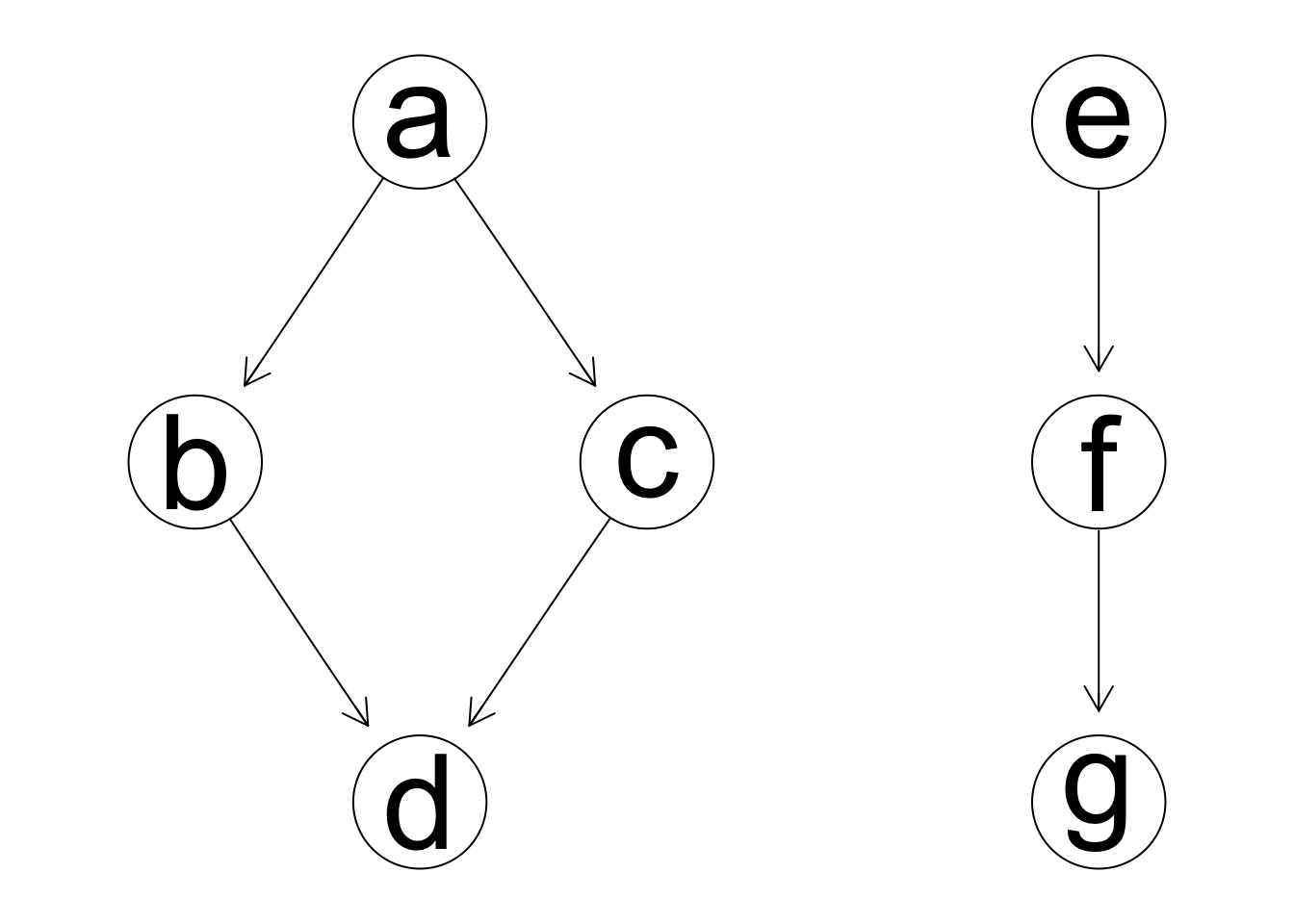
set.seed(280572)
n <- 300
a <- (rbinom(n, 1, 0.3))
b <- (rbinom(n, 1, a*0.1+(1-a)*0.8))
c <- (rbinom(n, 1, a*0.2+(1-a)*0.9))
d <- (rbinom(n, 1, b*c*0.9+ (1-b*c)*0.1 ))
e <- rbinom(n, 1, 0.4)
f <- rbinom(n, 1, e*0.3+(1-e)*0.6)
g <- rbinom(n, 1, f*0.2+(1-f)*0.8)
dat <- data.frame(factor(a),factor(b),factor(c),factor(d), factor(e), factor(f),
factor(g))
names(dat) <- c('a','b','c','d','e','f','g')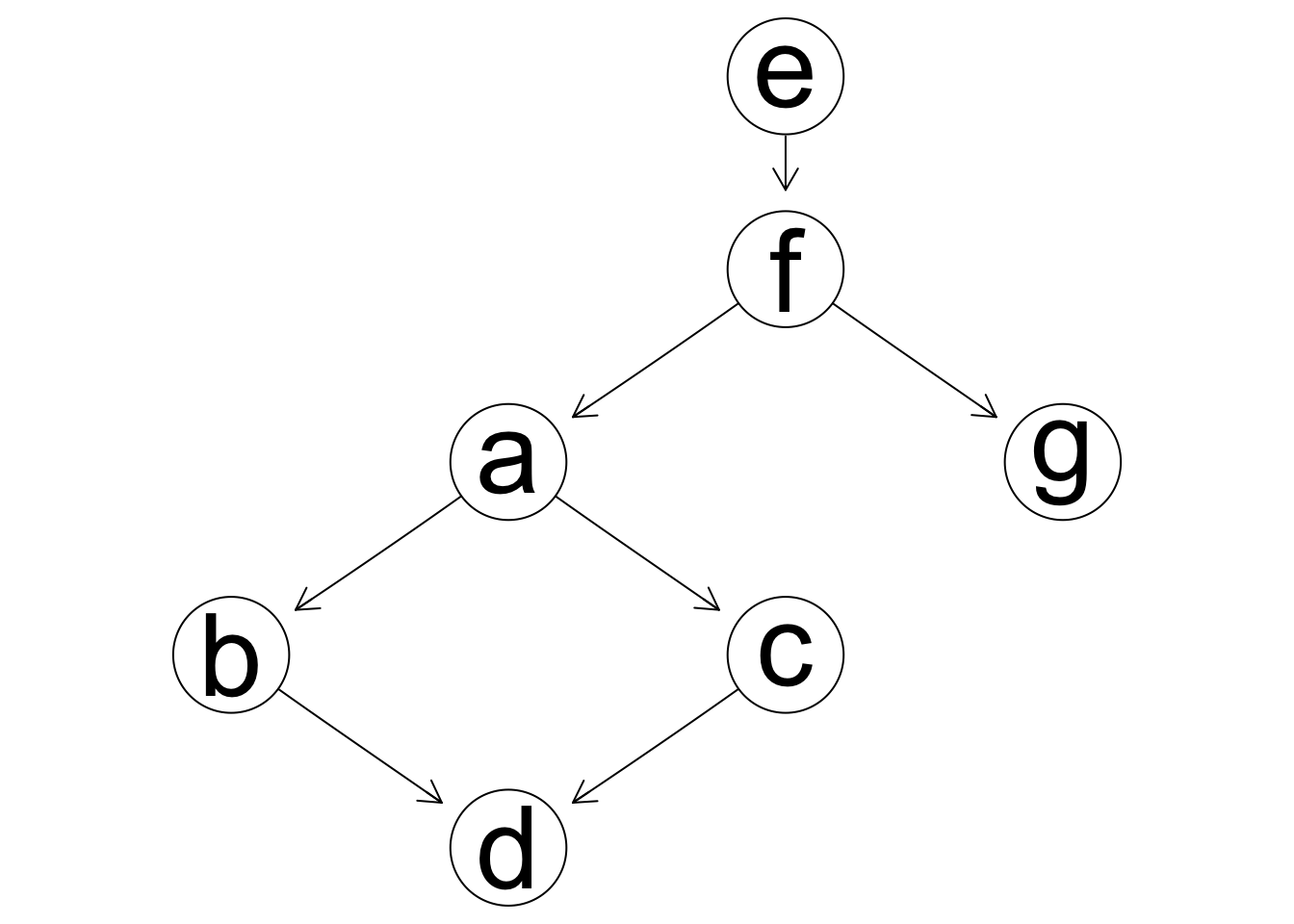
En este ejemplo, con el AIC obtenemos algunas aristas espurias, que en todo caso muestran relaciones aparentes débiles en los datos de entrenamiento. Nótese que AIC captura las relaciones importantes, y erra en cautela en cuanto a qué independencias están presentes en los datos.
2.4.3.1 Incorporando información acerca de la estructura
En algunos casos, tenemos información adicional de las posibles estructuras gráficas que son aceptables o deseables en los modelos que buscamos ajustar.
Esta información es muy valiosa cuando tenemos pocos datos o muchas variables (incluso puede ser crucial para obtener un modelo de buena calidad), y puede incorporarse en prohibiciones acerca de qué estructuras puede explorar el algoritmo.
Consideremos nuestro ejemplo anterior con considerablemente menos datos:
set.seed(28)
n <- 100
a <- (rbinom(n, 1, 0.2))
b <- (rbinom(n, 1, a*0.1+(1-a)*0.8))
c <- (rbinom(n, 1, a*0.2+(1-a)*0.9))
d <- (rbinom(n, 1, b*c*0.9+ (1-b*c)*0.1 ))
e <- rbinom(n, 1, 0.4)
f <- rbinom(n, 1, e*0.3+(1-e)*0.6)
g <- rbinom(n, 1, f*0.2+(1-f)*0.8)
dat <- data.frame(factor(a),factor(b),factor(c),factor(d), factor(e), factor(f),
factor(g))
names(dat) <- c('a','b','c','d','e','f','g')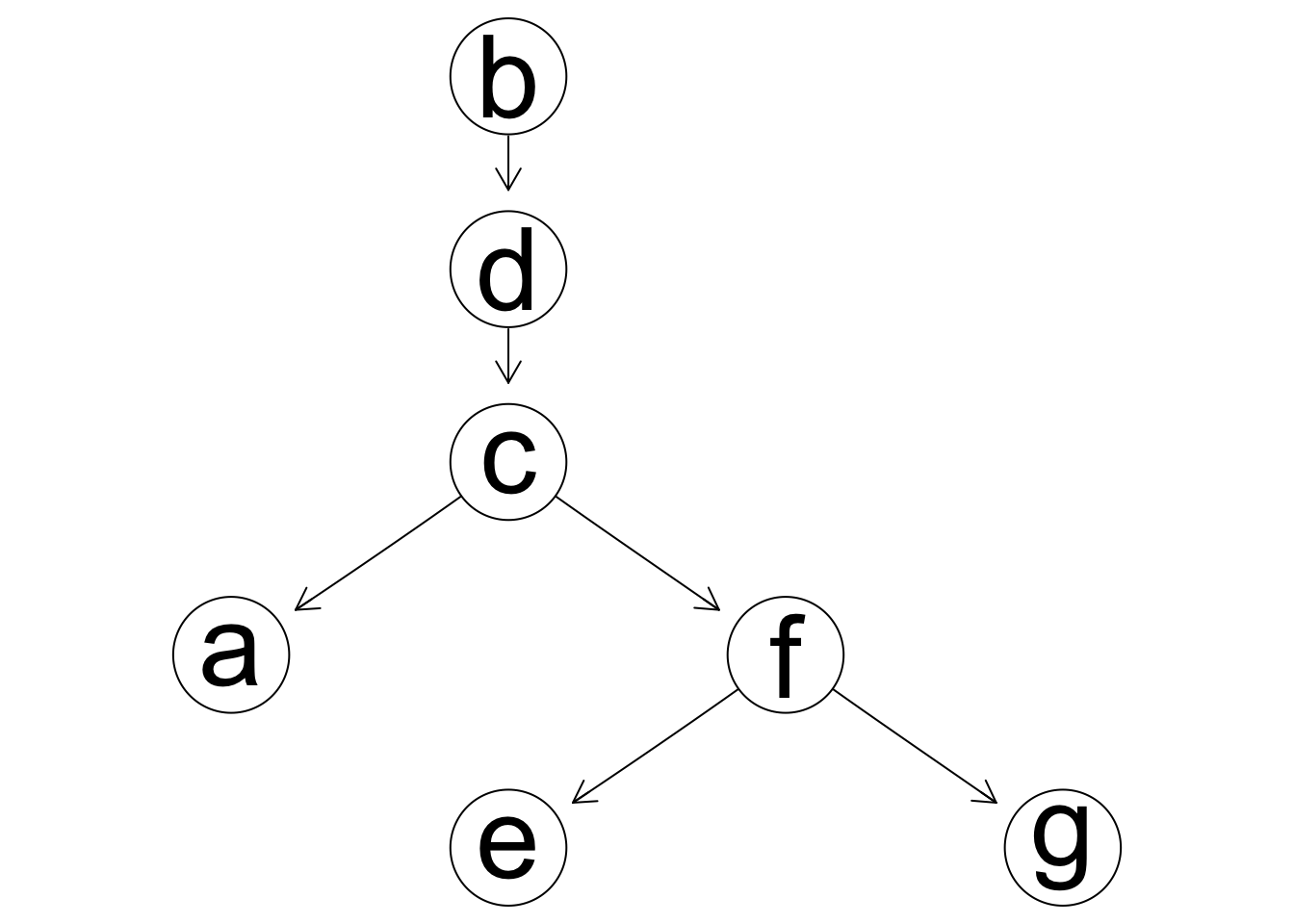
Nótese que en este ejemplo BIC falla en identificar una dependencia, y afirma que hay una independencia condicional entre a y d dado c. AIC sin embargo captura la dependencia con un modelo demasiado complejo (tres flechas espurias):
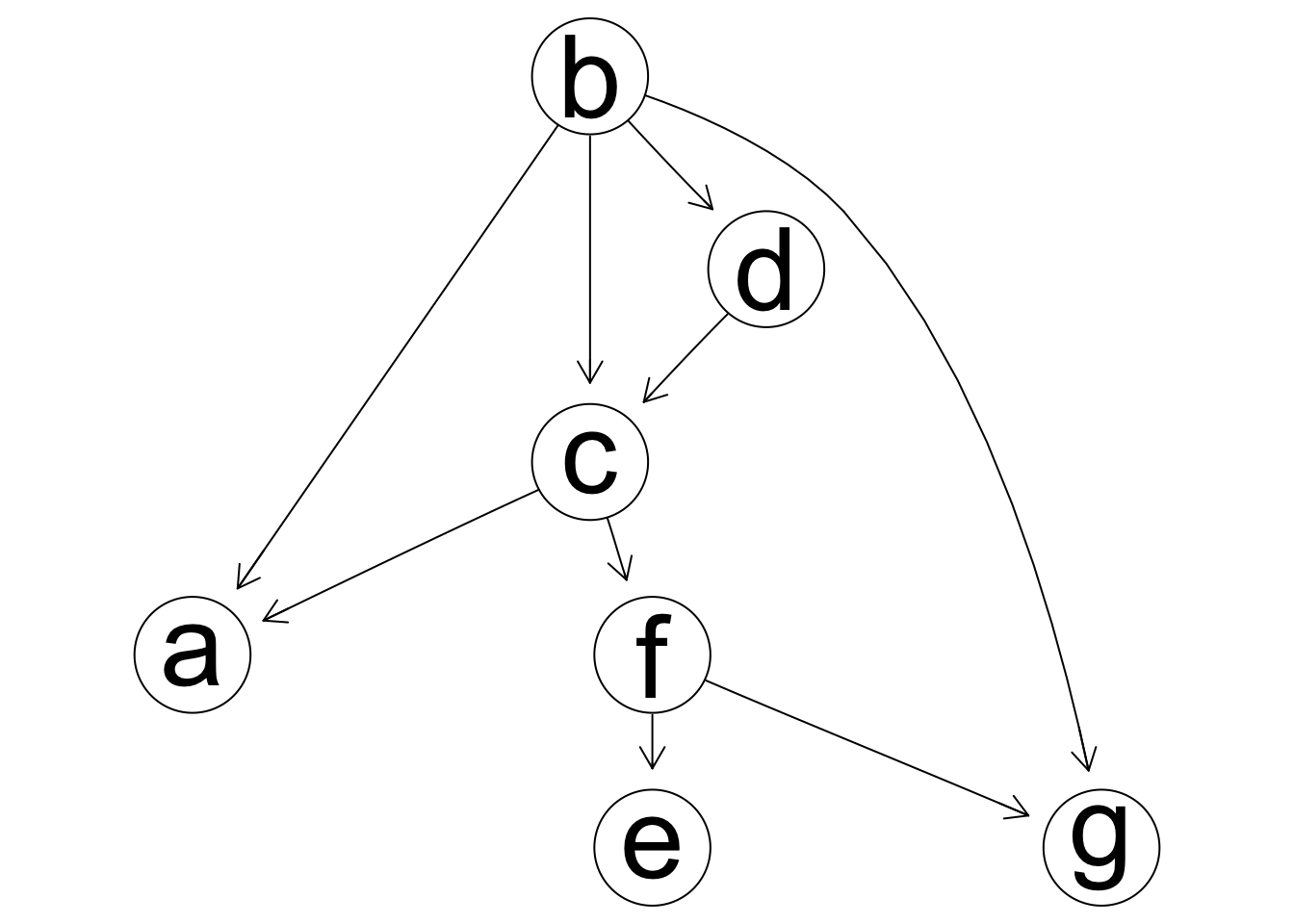
Sin embargo, si sabemos, por ejemplo, que no debe haber una flecha de c a f, y tiene que haber una de a a c, podemos mejorar nuestros modelos:
b.list <- data.frame(from=c('c','f'), to=c('f','c'))
w.list <- data.frame(from=c('a'), to=c('c'))
grafica.bic <- hc(dat, score='bic', blacklist=b.list, whitelist=w.list)
graphviz.plot(grafica.bic)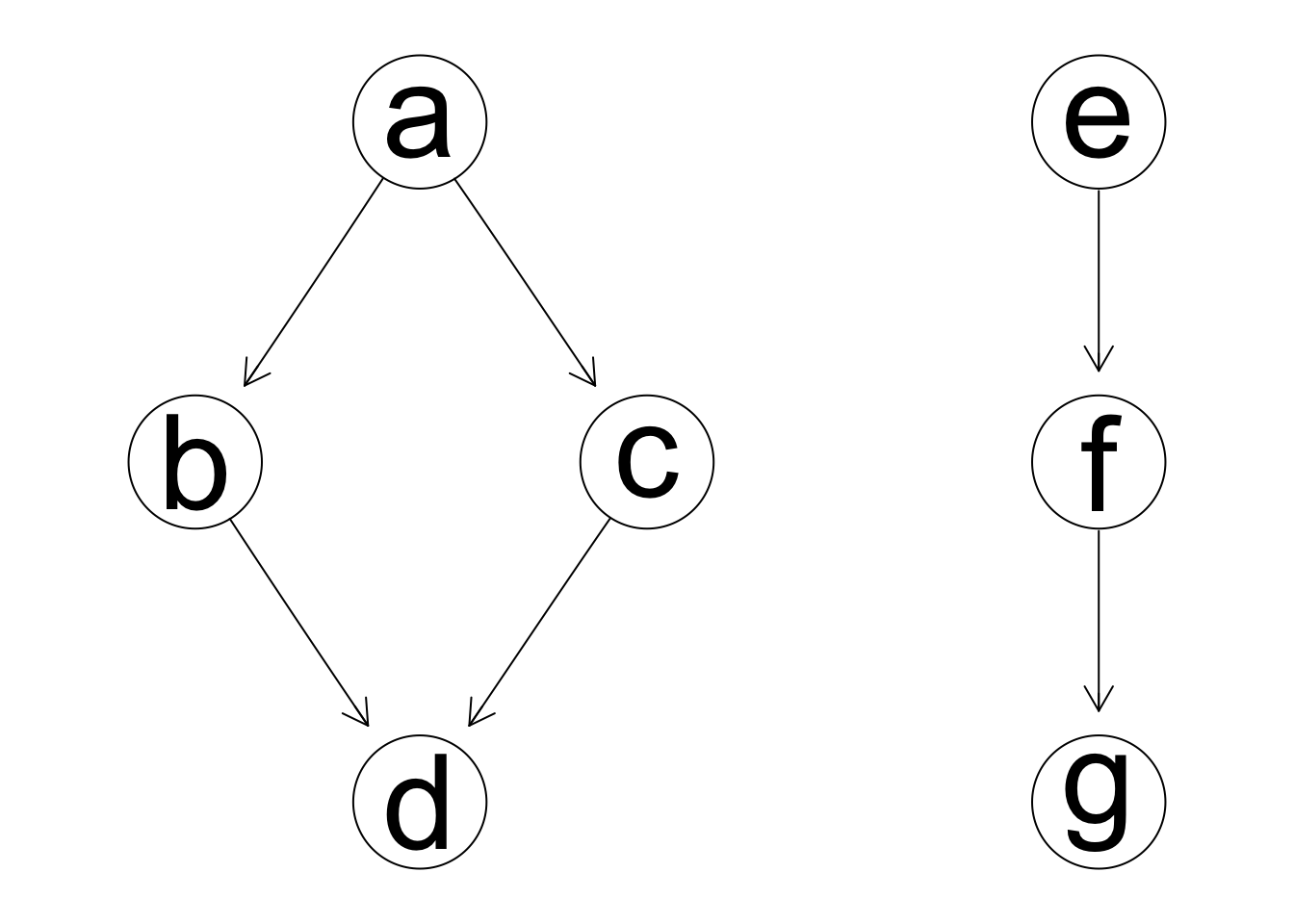
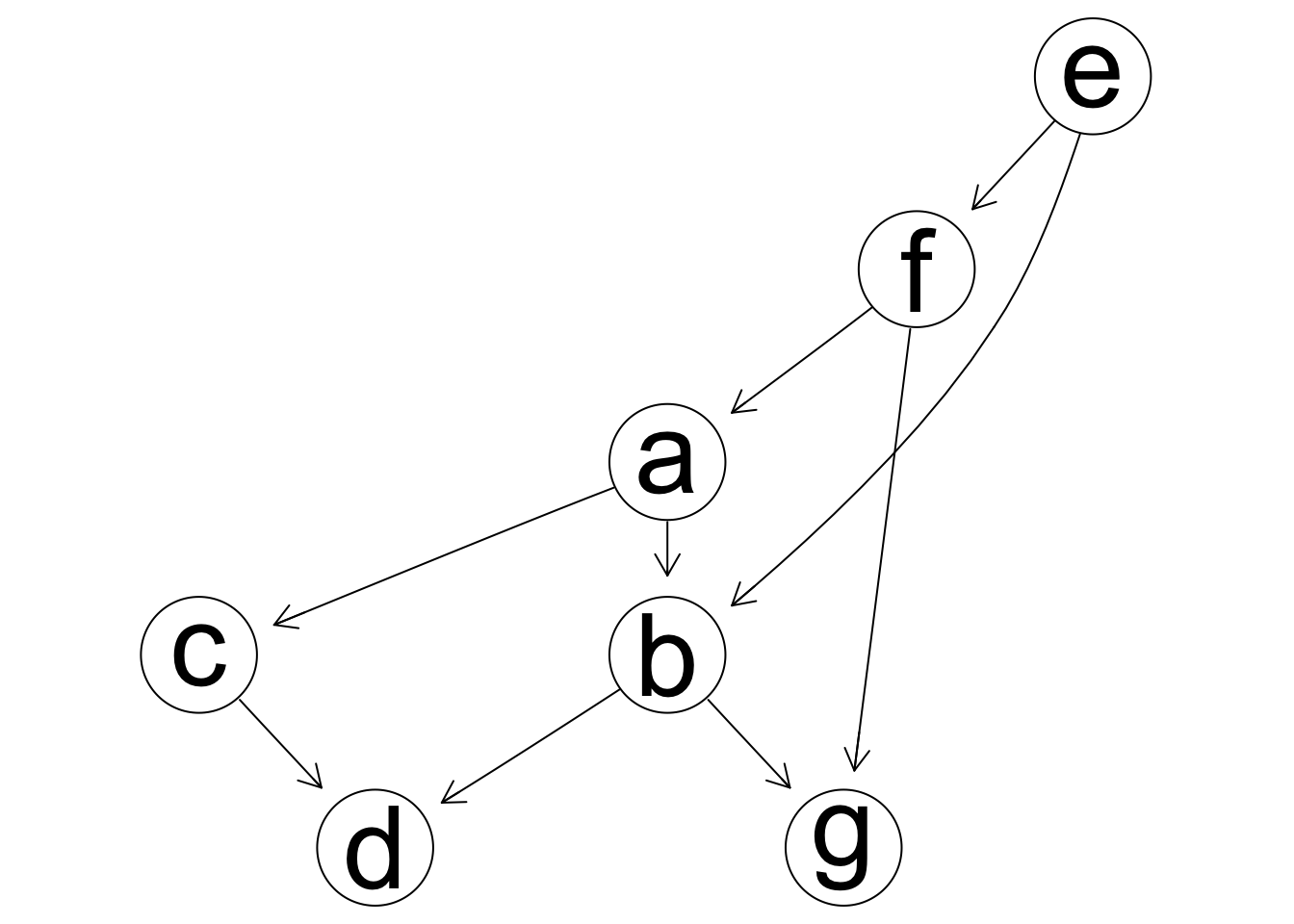
En este ejemplo estamos seguros de las aristas que forzamos. Muchas veces este no es el caso, y debemos tener cuidado:
Forzar la inclusión de una arista cuando esto no es necesario puede resultar en modelos demasiado complicados que incluyen estructuras espurias.
- Exclusión de muchas aristas puede provocar también modelos que ajustan mal y no explican los datos.
set.seed(28)
n <- 600
b <- (rbinom(n, 1, 0.4))
c <- (rbinom(n, 1, 0.7))
d <- (rbinom(n, 1, b*c*0.9+ (1-b*c)*0.1 ))
dat.x <- data.frame(factor(b),factor(c),factor(d))
names(dat.x) <- c('b','c','d')Supongamos que comenzamos agregando la arista \(d\to b\) (sentido incorrecto).
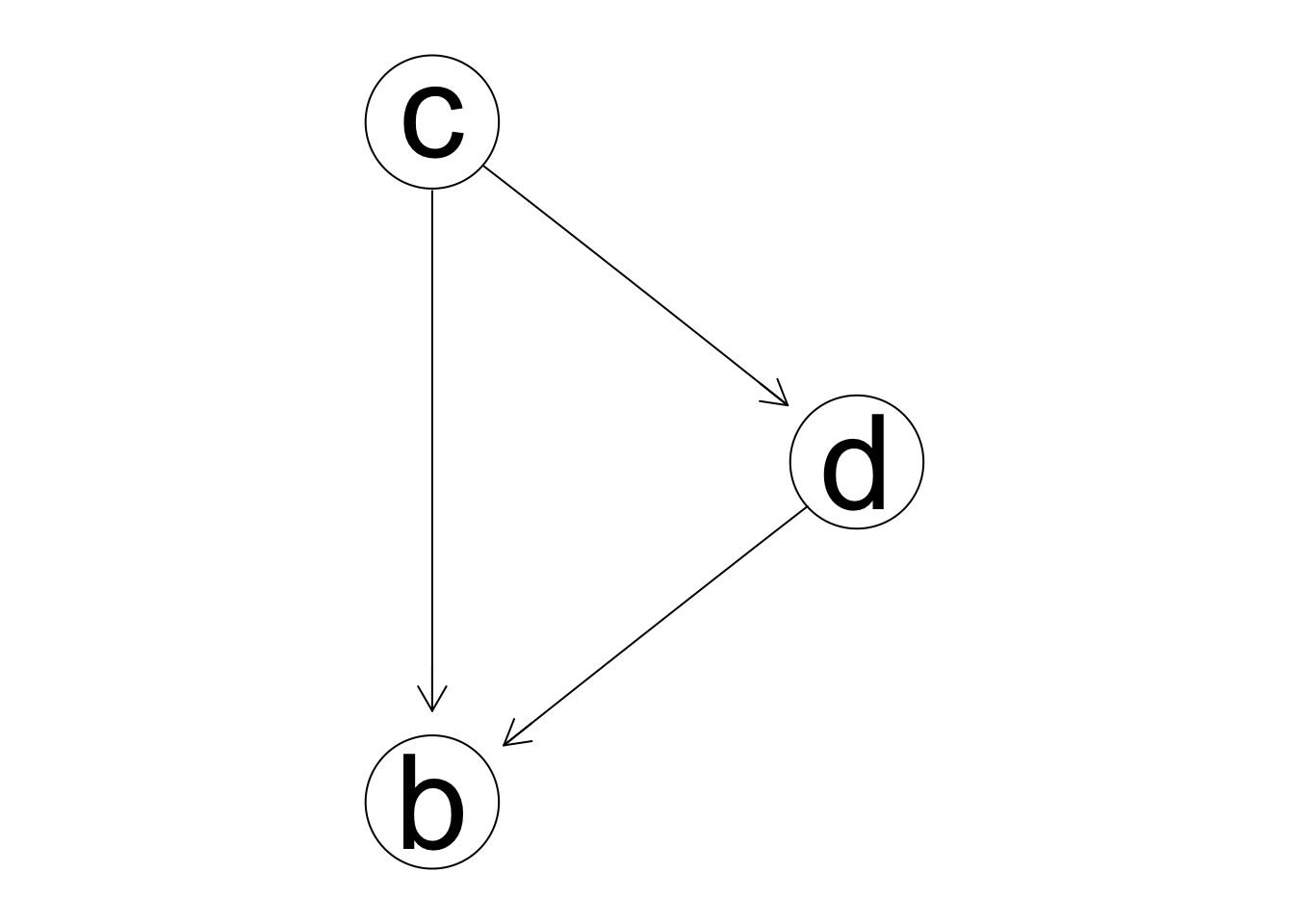
Y no aprendimos nada, pues cualquier conjunta se factoriza de esta manera.
2.4.3.2 Sentido de las aristas
Los métodos de score a lo más que pueden aspirar es a capturar la clase de equivalencia Markoviana de la conjunta que nos interesa (es decir, gráficas que tienen las mismas independencias, y que cubren a exactamente las mismas conjuntas que se factorizan sobre ellas). Esto implica que hay cierta arbitrariedad en la selección de algunas flechas.
En la siguiente gráfica, por ejemplo, ¿qué pasa si cambiamos el sentido de la flecha entre e y f?
set.seed(28)
n <- 500
a <- (rbinom(n, 1, 0.2))
b <- (rbinom(n, 1, a*0.1+(1-a)*0.8))
c <- (rbinom(n, 1, a*0.2+(1-a)*0.9))
d <- (rbinom(n, 1, b*c*0.9+ (1-b*c)*0.1 ))
e <- rbinom(n, 1, 0.4)
f <- rbinom(n, 1, e*0.3+(1-e)*0.6)
g <- rbinom(n, 1, f*0.2+(1-f)*0.8)
dat <- data.frame(factor(a),factor(b),factor(c),factor(d), factor(e), factor(f),
factor(g))
names(dat) <- c('a','b','c','d','e','f','g')
grafica.bic <- hc(dat, score='bic')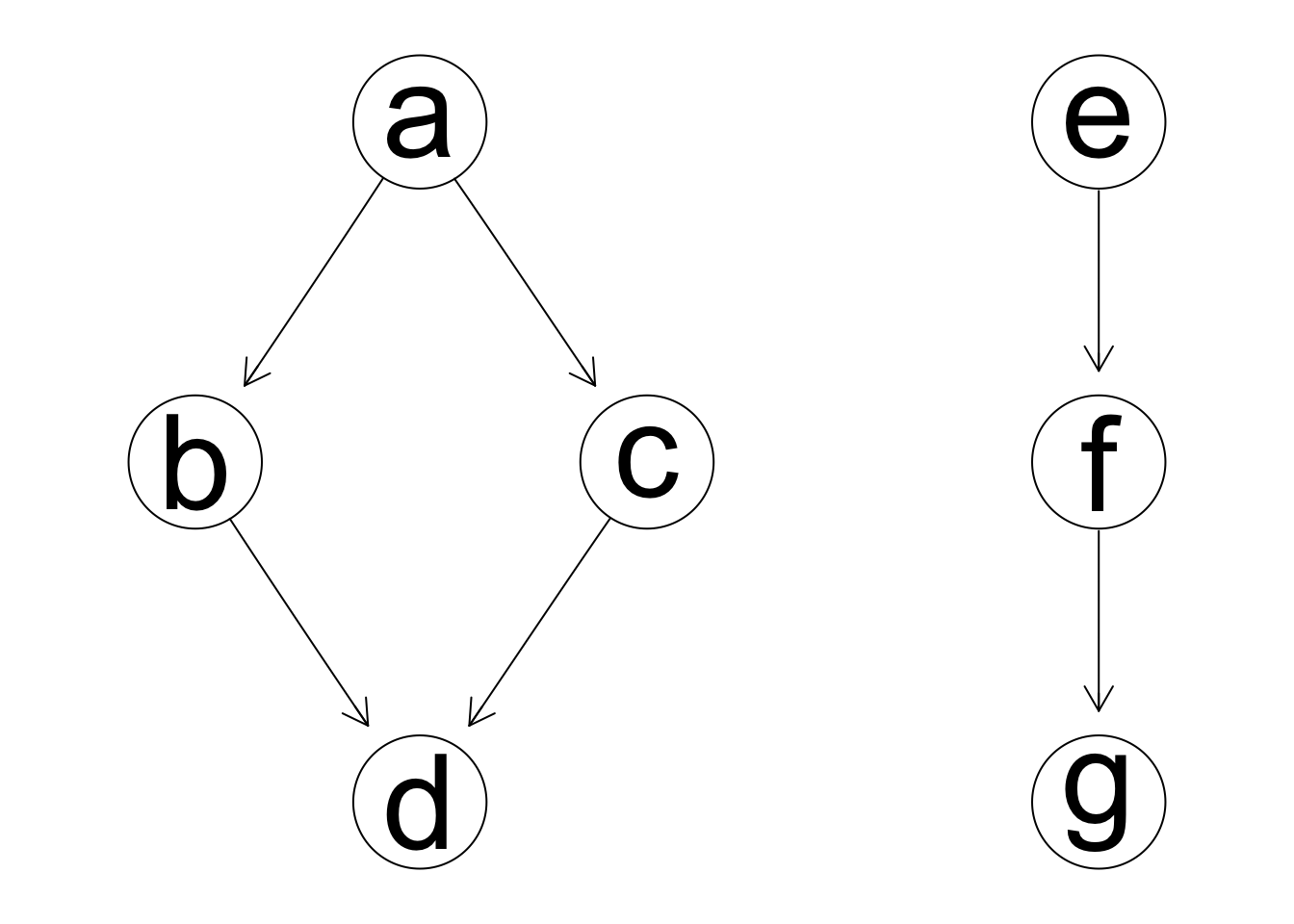
arcos <- grafica.bic$arcs
arcos
#> from to
#> [1,] "b" "d"
#> [2,] "a" "b"
#> [3,] "f" "g"
#> [4,] "a" "c"
#> [5,] "c" "d"
#> [6,] "e" "f"
arcos[3,] <- c('g','f')
arcos[6,] <- c('f','e')
grafica.2 <- grafica.bic
arcs(grafica.2) <- arcos
graphviz.plot(grafica.2)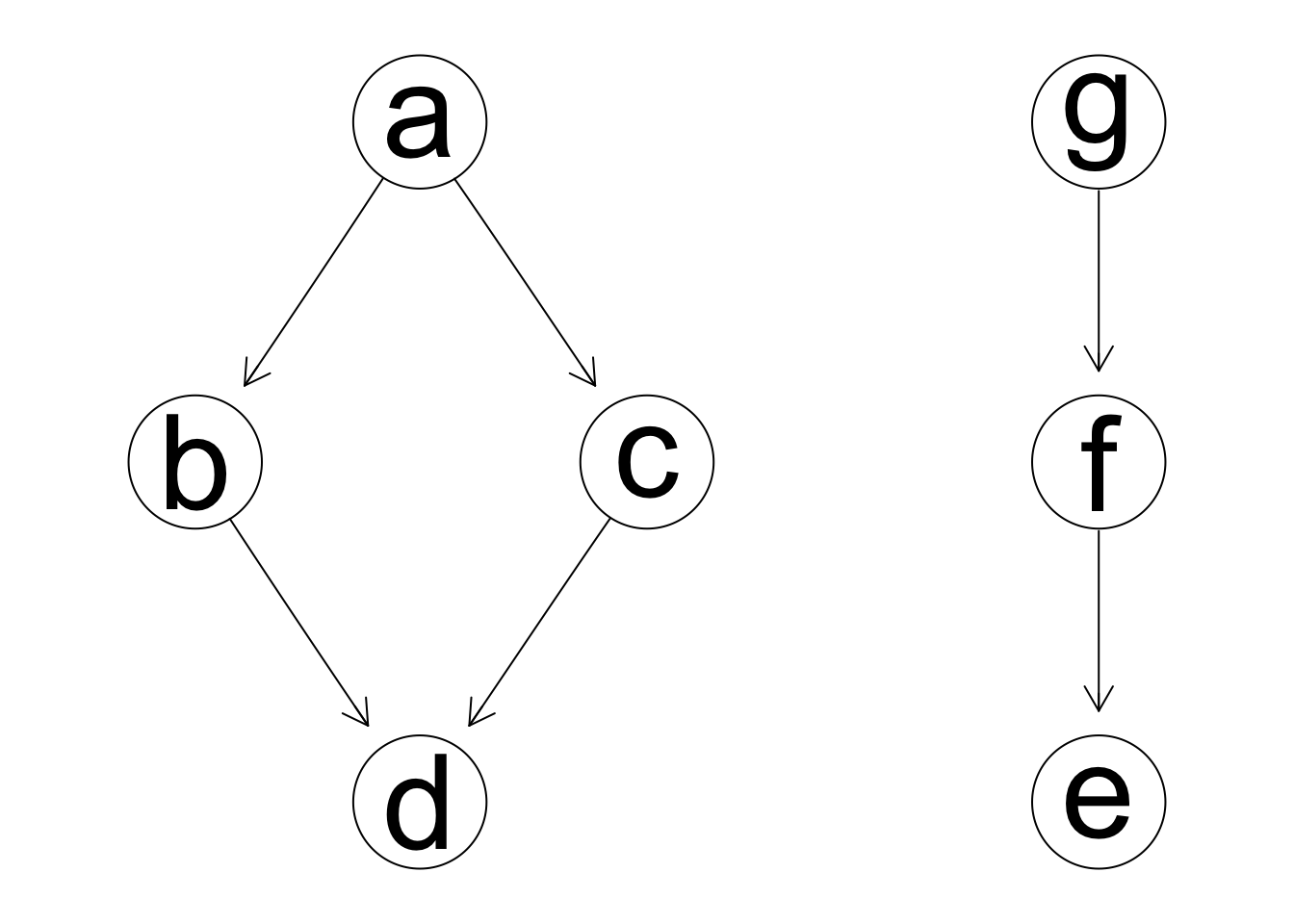
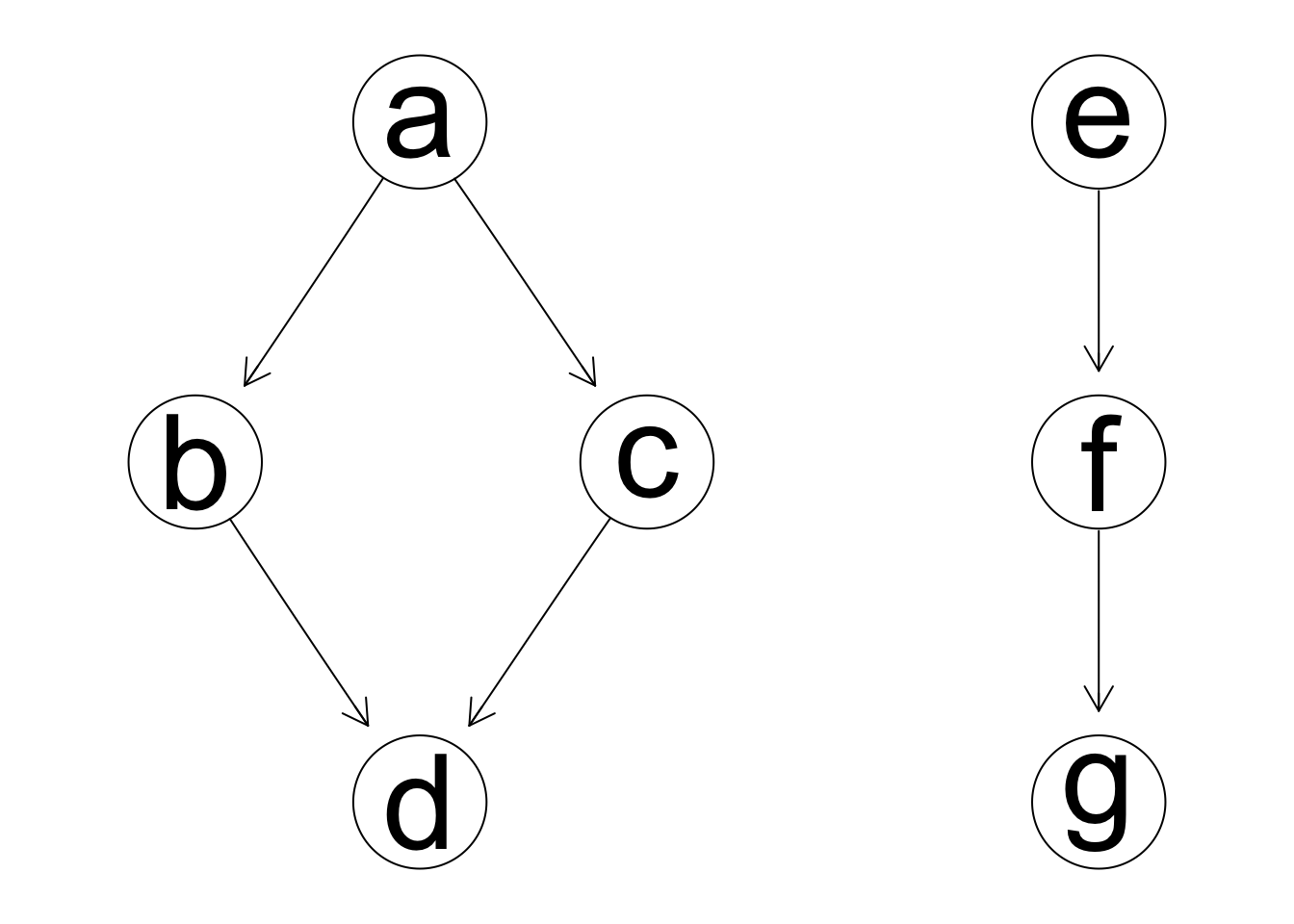
Vemos que no cambia la log-verosimilitud, ni ninguno de nuestros scores.
logLik(grafica.bic, data = dat)
#> [1] -1648.022
logLik(grafica.2, data = dat)
#> [1] -1648.022
BIC(grafica.bic, data = dat)
#> [1] -1691.525
BIC(grafica.2, data = dat)
#> [1] -1691.525
AIC(grafica.bic, data = dat)
#> [1] -1662.022
AIC(grafica.2, data = dat)
#> [1] -1662.022Esto implica que la dirección de estas flechas no puede determinarse solamente usando los datos. Podemos seleccionar la dirección de estas flechas por otras consideraciones, como explicaciones causales, temporales, o de interpretación. Los modelos son equivalentes, pero tienen una parametrización destinta.
 Mostrar que cambiar el sentido de una
flecha que colisiona en \(d\) (que es un colisionador no protegido) no da
scores equivalentes.
Mostrar que cambiar el sentido de una
flecha que colisiona en \(d\) (que es un colisionador no protegido) no da
scores equivalentes.
2.4.3.3 Variaciones de Hill-climbing
¿Cuál(es) de las siguientes opciones puede ser un problema para aprender la
estructura de la red?
a. Máximos locales.
b. Pasos discretos en los scores cuando se perturba la estructura.
c. Eliminar un arco no se puede expresar como una operación atómica en la
estructura.
d. Perturbaciones chicas en la estructura de la gráfica producen cambios muy
chicos o nulos en el score (plateaux).
¿Por que consideramos el operador de cambiar dirección como candidato en cada iteración si es el resultado de elminar un arco y añadir un arco? Eliminar un arco en hill-climbing tiende a disminuir el score de tal manera que el paso inicial de eliminar el arco no se tomará.
Revertir la dirección es una manera de evitar máximos locales.
Algunas modificaciones de hill-climbing consisten en incluir estrategias:
Inicios aleatorios: Si estamos en un plateaux, tomamos un número de pasos aleatorios y comenzamos a escalar nuevamente.
Tabu: Guardar una lista de los k pasos más recientes y la búsqueda no puede revertir estos pasos.