3.3 Redes Markovianas en Procesamiento de Imágenes
Una aplicación importante de redes markovianas es en procesamiento de imágenes, en esta diciplina las redes markovianas típicamente se conocen como Campos Aleatorios de Markov (Markov Random Fields) y se utilizan con distintos objetivos, por ejemplo, en la eliminación de ruido (eliminar lo borroso de una imagen), segmentación de imagenes o reconocimiento de objetos.
En la mayor parte de estas aplicaciones el modelo sigue una estructura de red Markoviana a pares donde los nodos corresponden a los pixeles y las aristas a interacciones entre pixeles adyacentes, por lo tanto cada pixel interior tiene exactamente cuatro vecinos. La definición de los potenciales depende de la aplicación, sin embargo es usual que los modelos se especifiquen en términos de energías (log-potenciales negativos) de tal manera que los valores representan penalizaciones y un valor menor corresponde a una configuración de mayor probabilidad.
En el caso de elimincación de ruido el objetivo es recuperar el verdadero valor de los pixeles dado que algunos pixeles presentan ruido. Denotemos por el verdadero valor del pixel (este es el valor que buscamos inferir) y por el valor del pixel que observamos (que presenta ruido). En este problema suponemos una correlación fuerte entre y , además de haber correlación positiva entre pixeles vecinos y . La gráfica correspondiente a este modelo se muestra a continución.
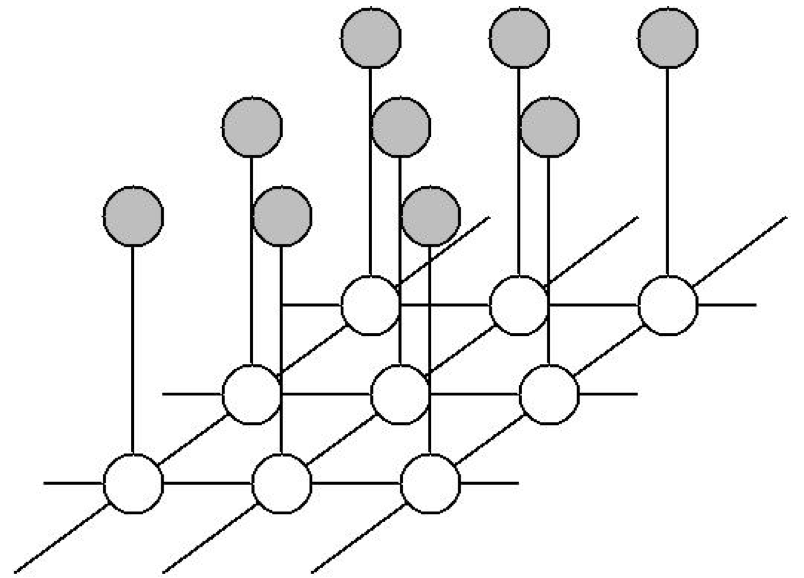
La gráfica muestra dos tipos de cliques, cada uno con dos variables. Los cliques de la forma a la que asociaremos una función de energía que cumple con el efecto de asignar menor energía (y por tanto alentando mayor probabilidad) cuando el valor de las variables es cercano. Por otra parte, los cliques de la forma donde y son índices de pixeles vecinos, tienen asociada una función de energía que penaliza diferencias entre pixeles vecinos.
Veamos un ejemplo sencillo donde la imagen ruidosa esta descrita por una matriz de pixeles que toman uno de dos valores , el índice indica el pixel. Supongamos que la imagen ruidosa se obtiene de una imagen libre de ruido que se descibe por una matriz donde los pixeles toman los valores , el ruido se añade cambiando el signo de los pixeles de la imagen original con una probabilidad baja. La figura de abajo es un ejemplo donde se cambio el signo de los pixeles con probabilidad 0.10.

Capturamos la relación entre y asociando la función de energía donde es una constante positiva, observemos que la energía es menor cuando y tienen el mismo signo y mayor cuando tienen el signo opuesto, ¿Cómo se traduce esto en los potenciales? En el caso de cliques que relacionan pixeles vecinos , elegimos la función de energía donde es una constante positiva, el comportamiento de esta función es análogo a la función que relaciona y .
Finalmente, añadimos el término para cada pixel cuya función es
sesgar el modelo hacia valores de pixeles que compartan el mismo signo.
La función de energía completa para el modelo toma la forma:
que determina la distribución conjunta:
Una vez definidas las funciones de energía se asignan a los valores de los
pixeles observados en la imagen ruidosa que define implícitamente una
distribución condicional sobre los pixeles libres de ruido. Buscamos
entonces encontrar una imagen de probabilidad alta (idealmente máxima)
condicional a la imagen observada.
Para recuperar la imagen utilizamos una técnica iterativa llamada Modas
Condicionales Iteradas (o ICM por sus siglas en inglés) que es una aplicaciónn de ascenso de gradiente:
- Se inicializan las variables igualando para toda .
- Para cada nodo evaluamos la energía total para cada estado y .
- Actualizamos el valor que toma al estado que minimiza la energía. Repetimos el procedimiento en un nuevo nodo hasta que se satisfaga algún criterio de paro. Este paso puede mantener la probabilidad de constante o incrementarla si cambiamos el valor que toma .
- Repetimos el paso 2 y 3 hasta satisfacer algún criterio de paro.
La función de energía es en principio arbitraria, sin embargo, existen varias alternativas estándar para procesamiento de imagenes, por ejemplo, si la imagen se encuentra en escala de grises, los pixeles pueden tomar cualquiera de 256 valores (8 bits) y una función de energía apropiada es la siguiemte:
donde representa la creencia de que la imagen está corrompida por ruido con una varianza .
library(bmp)
library(pixmap)
library(jpeg)
perro <- readJPEG("img/perrito.jpg", native = FALSE)[,,1]
pr <- pixmapGrey(perro)
plot(pr)
perro_mat <- 255 * perro
# Añadir ruido
noise <- function(image, sdev = 20){
dimension <- dim(image)
a <- round(c(image) + rnorm(n = length(image), 0, sd = sdev))
a[a < 0] <- 0
a[a > 255] <- 255
image_blur <- array(data = a, dim = dimension)
}
perro_n <- noise(perro_mat)
pr_n <- pixmapGrey(perro_n / 255)
plot(pr_n)
icm <- function(image, sdev = 25, max.diff = 200, weight.diff = 0.15,
iterations = 20){
# sdev: error estándar del ruido gaussiano.
# max_diff: contribución máxima al potencial de la diferencia entre los valores
# de dos pixeles vecinos
# weight_diff: es la ponderación asociada al componente del potencial
# debida a la diferencia entre los valores de pixeles vecinos.
# iter: es el número de iteraciones.
# Siempre tengo dos imágenes, en cada iteración se alternan entre imagen
# fuente e imagen destino.
dimension <- dim(image)
buffer <- array(0, dim = c(dimension, 2))
buffer[, , 1] <- image
s <- 2
d <- 1
# Este valor siempre será mayor que el potencial de cualquier configuración
# de valores de pixeles
V.max = (dimension[1] * dimension[2]) * ((256 ^ 2) / (2 * sdev) +
4 * weight.diff * max.diff)
for(i in 1:iterations){
# Switch source and destination buffers.
if(s == 1){
s = 2;
d = 1;
}
else{
s = 1;
d = 2;
}
# Variamos cada pixel individualmente para encontrar los valores que
# minimizan los potenciales locales.
for(r in 1:dimension[1]){
for(c in 1:dimension[2]){
V.local = V.max
min.val = -1
for(val in 0:255){
# Componente del potencial correspondiente a los datos observados.
V.data = (val - image[r,c])^2 / (2 * sdev)
# Componente del potencial correspondiente a la diferencia entre los
# pixeles vecinos
V.diff = 0
if(r > 1){
V.diff = V.diff + min((val - buffer[r-1,c,s])^2, max.diff)
}
if(r < dimension[1]){
V.diff = V.diff + min((val - buffer[r+1,c,s])^2, max.diff)
}
if(c > 1){
V.diff = V.diff + min((val - buffer[r,c-1,s])^2, max.diff)
}
if(c < dimension[2]){
V.diff = V.diff + min((val - buffer[r,c+1,s])^2, max.diff)
}
V.current = V.data + weight.diff * V.diff
if(V.current < V.local){
min.val = val
V.local = V.current
}
}
buffer[r, c, d] = min.val
}
}
}
buffer[,,d]
}
perro_c <- icm(perro_n)
#writeJPEG(perro_n / 255, "img/p_ruido.jpg")
#writeJPEG(perro_c / 255, "img/p_recuperado_2.jpg")
pr_c <- pixmapGrey(perro_c/255)
plot(pr_c)
El siguiente es un ejemplo de clasificación de pixeles usando redes markovianas. En este ejemplo se tienen dos imágenes satelitales (1000x1000 pixeles cada una) del mismo lugar, tomadas en diferentes tiempos y se busca encontrar cambios. Los resultados se muestran abajo, la tercera imagen es la imagen de diferencias (usando IMAD_MAF) y las imágenes de abajo corresponden a dos algoritmos de detección de cambios, el primero es mezclas gaussianas y da resultados muy ruidosos. El segundo utiliza campos aleatorios de Markov y resulta en cambios menos ruidosos.

Ligas relacionadas a procesamiento de imágenes
Boykov, Funka-Lea Graph Cuts and Efficient N-D Image Segmentation.
Computer Vision Research Group, University of Western Ontario.
PyMaxflow, librería de python (stereograma y ejemplo binario).
Blake y Kohli handouts, Introduction to MRF.