2.2 Redes bayesianas
Ahora podemos definir red bayesiana:
Una red bayesiana es una gráfica GAD junto con una distribución de probabilidad particular que se factoriza sobre .
Dado que se factoriza sobre , podemos usar la factorización para evitar dar explícitamente la conjunta sobre todas las posibles combinaciones de las variables. Es decir, podemos usar la parametrización dada por la factorización en condicionales.
Ejemplo. Sea la siguiente gráfica
gr <- graph(c(1,2,3,2,2,4))
plot(gr,
vertex.label=c('llueve', 'mojado', 'regar', 'piso'),
layout = matrix(c(0, 1, 1, 0, 0, -1, 2, 0), byrow = TRUE, ncol = 2),
vertex.size = 20, vertex.color = 'salmon', vertex.label.cex = 1.2,
vertex.label.color = 'gray40', vertex.frame.color = NA, asp = 0.5,
edge.arrow.size = 1)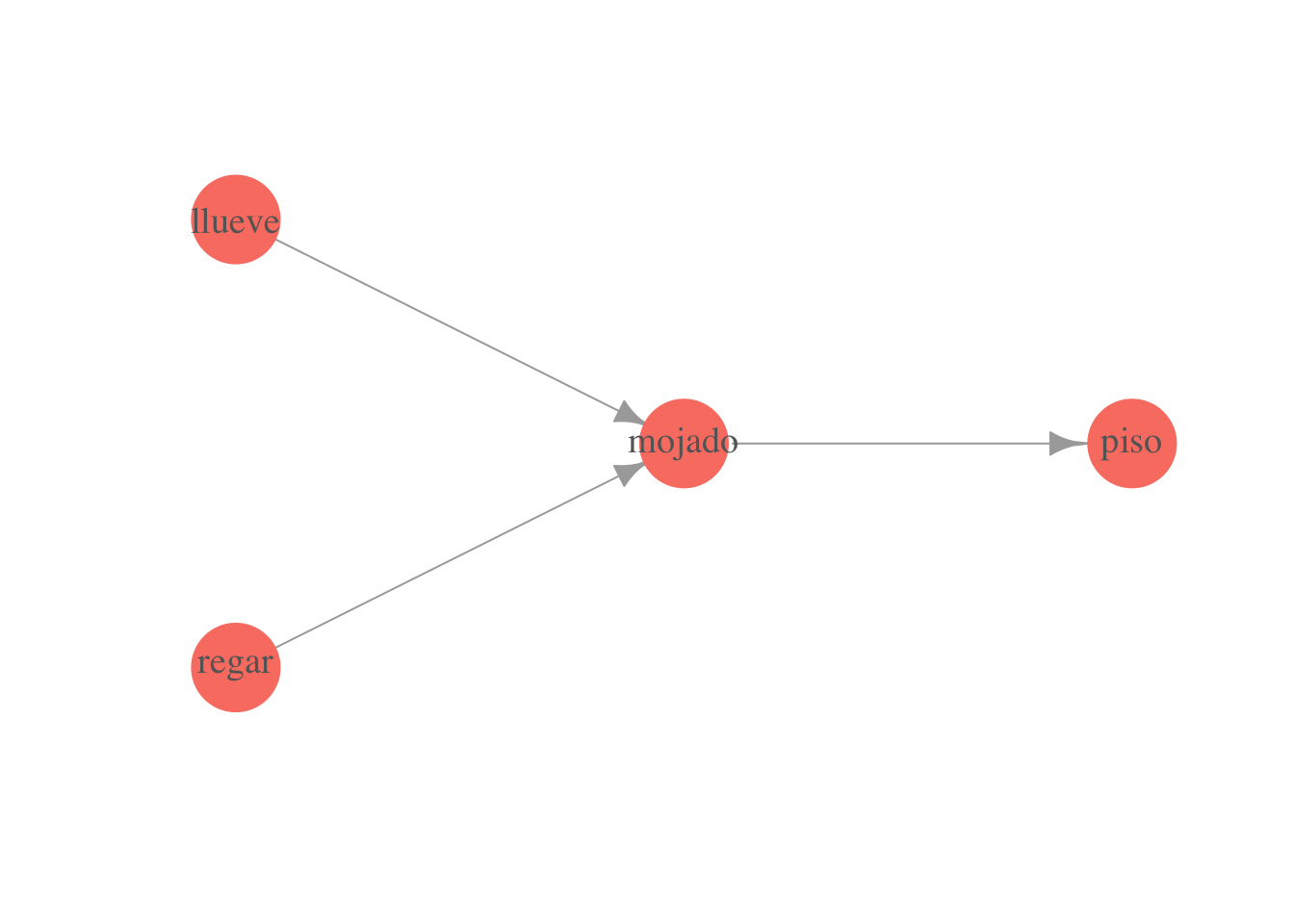
La conjunta ( es piso resbaloso) se factoriza como
En este ejemplo construiremos la red como si fuéramos los expertos. Esta es una manera de construir redes que ha resultado útil y exitosa en varias áreas (por ejemplo diagnóstico).
De forma que podemos construir una red bayesiana simplemente dando los valores de cada factor. En nuestro ejemplo, empezamos por las marginales de y :
llueve <- c('No', 'Sí')
p_llueve <- data.frame(llueve = factor(llueve, levels= c("No", "Sí")),
prob_l = c(0.9, 0.1))
p_llueve
#> llueve prob_l
#> 1 No 0.9
#> 2 Sí 0.1
regar <- c('Apagado', 'Prendido')
p_regar <- data.frame(regar = factor(regar, levels = c('Apagado', 'Prendido')),
prob_r = c(0.7, 0.3))
p_regar
#> regar prob_r
#> 1 Apagado 0.7
#> 2 Prendido 0.3Ahora establecemos la condicional de mojado dado lluvia y regar:
mojado <- c('Mojado','Seco')
# los niveles son todas las combinaciones de los valores de las variables
niveles <- expand.grid(llueve = llueve, regar = regar, mojado = mojado)
# mojado|lluve,regar
p_mojado_lr <- data.frame(niveles, prob_m = NA)
p_mojado_lr$prob_m[1:4] <- c(0.02, 0.6, 0.7, 0.9)
p_mojado_lr$prob_m[5:8]<- 1 - p_mojado_lr$prob_m[1:4]
p_mojado_lr
#> llueve regar mojado prob_m
#> 1 No Apagado Mojado 0.02
#> 2 Sí Apagado Mojado 0.60
#> 3 No Prendido Mojado 0.70
#> 4 Sí Prendido Mojado 0.90
#> 5 No Apagado Seco 0.98
#> 6 Sí Apagado Seco 0.40
#> 7 No Prendido Seco 0.30
#> 8 Sí Prendido Seco 0.10Y finalmente la condicional de piso resbaloso dado piso mojado:
p_piso_mojado <- data.frame(expand.grid(
piso = c('Muy.resbaladizo', 'Resbaladizo', 'Normal'),
mojado=c('Mojado','Seco')))
p_piso_mojado
#> piso mojado
#> 1 Muy.resbaladizo Mojado
#> 2 Resbaladizo Mojado
#> 3 Normal Mojado
#> 4 Muy.resbaladizo Seco
#> 5 Resbaladizo Seco
#> 6 Normal Seco
p_piso_mojado$prob_p <- c(0.3, 0.6, 0.1, 0.02, 0.3, 0.68)
p_piso_mojado
#> piso mojado prob_p
#> 1 Muy.resbaladizo Mojado 0.30
#> 2 Resbaladizo Mojado 0.60
#> 3 Normal Mojado 0.10
#> 4 Muy.resbaladizo Seco 0.02
#> 5 Resbaladizo Seco 0.30
#> 6 Normal Seco 0.68Con esta información podemos calcular la conjunta. En este caso, como el problema es relativamente chico, podemos hacerlo explícitamente para todos los niveles:
p_1 <- inner_join(p_piso_mojado, p_mojado_lr)
#> Joining, by = "mojado"
p_2 <- inner_join(p_1, p_llueve)
#> Joining, by = "llueve"
p_conj <- inner_join(p_2, p_regar)
#> Joining, by = "regar"
p_conj$prob <- p_conj$prob_p * p_conj$prob_m * p_conj$prob_l * p_conj$prob_r
p_conj
#> piso mojado prob_p llueve regar prob_m prob_l prob_r
#> 1 Muy.resbaladizo Mojado 0.30 No Apagado 0.02 0.9 0.7
#> 2 Muy.resbaladizo Mojado 0.30 Sí Apagado 0.60 0.1 0.7
#> 3 Muy.resbaladizo Mojado 0.30 No Prendido 0.70 0.9 0.3
#> 4 Muy.resbaladizo Mojado 0.30 Sí Prendido 0.90 0.1 0.3
#> 5 Resbaladizo Mojado 0.60 No Apagado 0.02 0.9 0.7
#> 6 Resbaladizo Mojado 0.60 Sí Apagado 0.60 0.1 0.7
#> 7 Resbaladizo Mojado 0.60 No Prendido 0.70 0.9 0.3
#> 8 Resbaladizo Mojado 0.60 Sí Prendido 0.90 0.1 0.3
#> 9 Normal Mojado 0.10 No Apagado 0.02 0.9 0.7
#> 10 Normal Mojado 0.10 Sí Apagado 0.60 0.1 0.7
#> 11 Normal Mojado 0.10 No Prendido 0.70 0.9 0.3
#> 12 Normal Mojado 0.10 Sí Prendido 0.90 0.1 0.3
#> 13 Muy.resbaladizo Seco 0.02 No Apagado 0.98 0.9 0.7
#> 14 Muy.resbaladizo Seco 0.02 Sí Apagado 0.40 0.1 0.7
#> 15 Muy.resbaladizo Seco 0.02 No Prendido 0.30 0.9 0.3
#> 16 Muy.resbaladizo Seco 0.02 Sí Prendido 0.10 0.1 0.3
#> 17 Resbaladizo Seco 0.30 No Apagado 0.98 0.9 0.7
#> 18 Resbaladizo Seco 0.30 Sí Apagado 0.40 0.1 0.7
#> 19 Resbaladizo Seco 0.30 No Prendido 0.30 0.9 0.3
#> 20 Resbaladizo Seco 0.30 Sí Prendido 0.10 0.1 0.3
#> 21 Normal Seco 0.68 No Apagado 0.98 0.9 0.7
#> 22 Normal Seco 0.68 Sí Apagado 0.40 0.1 0.7
#> 23 Normal Seco 0.68 No Prendido 0.30 0.9 0.3
#> 24 Normal Seco 0.68 Sí Prendido 0.10 0.1 0.3
#> prob
#> 1 0.003780
#> 2 0.012600
#> 3 0.056700
#> 4 0.008100
#> 5 0.007560
#> 6 0.025200
#> 7 0.113400
#> 8 0.016200
#> 9 0.001260
#> 10 0.004200
#> 11 0.018900
#> 12 0.002700
#> 13 0.012348
#> 14 0.000560
#> 15 0.001620
#> 16 0.000060
#> 17 0.185220
#> 18 0.008400
#> 19 0.024300
#> 20 0.000900
#> 21 0.419832
#> 22 0.019040
#> 23 0.055080
#> 24 0.002040
sum(p_conj$prob)
#> [1] 1Usamos el paquete bnlearn para construir el objeto que corresponde a esta red bayesiana:
# nodos
graf_jardin <- empty.graph(c('llueve', 'regar', 'mojado', 'piso'))
# arcos
arcs(graf_jardin) <- matrix(c('llueve', 'mojado', 'regar', 'mojado', 'mojado',
'piso'), ncol = 2, byrow = T)
node.ordering(graf_jardin)
#> [1] "llueve" "regar" "mojado" "piso"
plot(graf_jardin)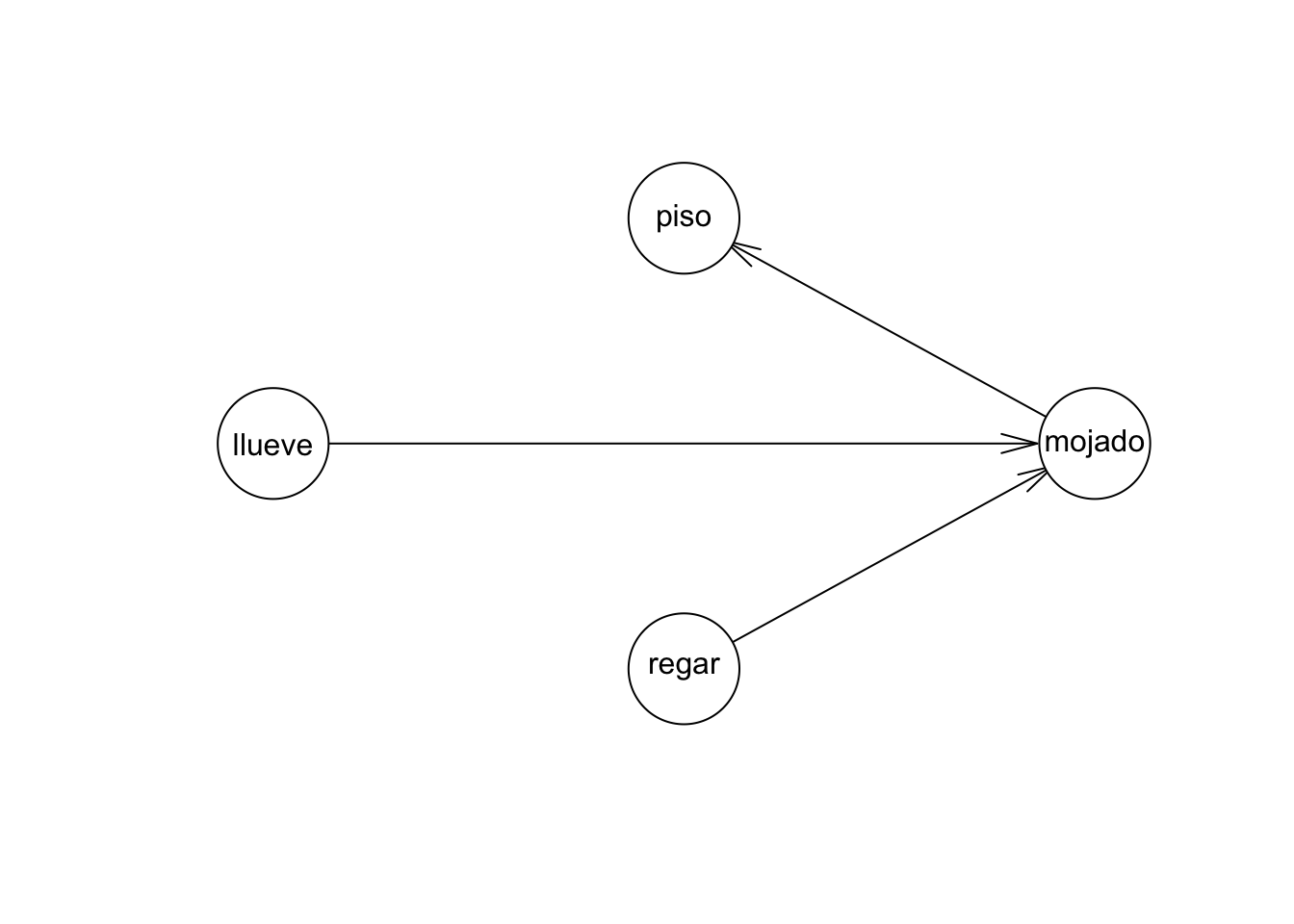
modelo_jardin <- bn.fit(graf_jardin,
data = data.frame(p_conj[, c('llueve', 'regar', 'mojado', 'piso')]))Y este es el objeto que representa nuestra red (aunque falta corregir las probabilidades):
str(modelo_jardin)
#> List of 4
#> $ llueve:List of 4
#> ..$ node : chr "llueve"
#> ..$ parents : chr(0)
#> ..$ children: chr "mojado"
#> ..$ prob : 'table' num [1:2(1d)] 0.5 0.5
#> .. ..- attr(*, "dimnames")=List of 1
#> .. .. ..$ : chr [1:2] "No" "Sí"
#> ..- attr(*, "class")= chr "bn.fit.dnode"
#> $ regar :List of 4
#> ..$ node : chr "regar"
#> ..$ parents : chr(0)
#> ..$ children: chr "mojado"
#> ..$ prob : 'table' num [1:2(1d)] 0.5 0.5
#> .. ..- attr(*, "dimnames")=List of 1
#> .. .. ..$ : chr [1:2] "Apagado" "Prendido"
#> ..- attr(*, "class")= chr "bn.fit.dnode"
#> $ mojado:List of 4
#> ..$ node : chr "mojado"
#> ..$ parents : chr [1:2] "llueve" "regar"
#> ..$ children: chr "piso"
#> ..$ prob : 'table' num [1:2, 1:2, 1:2] 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
#> .. ..- attr(*, "dimnames")=List of 3
#> .. .. ..$ mojado: chr [1:2] "Mojado" "Seco"
#> .. .. ..$ llueve: chr [1:2] "No" "Sí"
#> .. .. ..$ regar : chr [1:2] "Apagado" "Prendido"
#> ..- attr(*, "class")= chr "bn.fit.dnode"
#> $ piso :List of 4
#> ..$ node : chr "piso"
#> ..$ parents : chr "mojado"
#> ..$ children: chr(0)
#> ..$ prob : 'table' num [1:3, 1:2] 0.333 0.333 0.333 0.333 0.333 ...
#> .. ..- attr(*, "dimnames")=List of 2
#> .. .. ..$ piso : chr [1:3] "Muy.resbaladizo" "Resbaladizo" "Normal"
#> .. .. ..$ mojado: chr [1:2] "Mojado" "Seco"
#> ..- attr(*, "class")= chr "bn.fit.dnode"
#> - attr(*, "class")= chr [1:2] "bn.fit" "bn.fit.dnet"Ahora pondremos las probabilidades condicionales correctas (también llamados modelos locales):
tab_1 <- table(p_conj$llueve)
tab_1[c(1, 2)] <- p_llueve[, 2]
tab_1
#>
#> No Sí
#> 0.9 0.1
modelo_jardin$llueve <- tab_1
tab_2 <- table(p_conj$regar)
tab_2[c(1,2)] <- p_regar[,2]
tab_2
#>
#> Apagado Prendido
#> 0.7 0.3
modelo_jardin$regar <- tab_2
tab_3 <- xtabs(prob_m ~ mojado + llueve + regar, data = p_mojado_lr)
tab_3
#> , , regar = Apagado
#>
#> llueve
#> mojado No Sí
#> Mojado 0.02 0.60
#> Seco 0.98 0.40
#>
#> , , regar = Prendido
#>
#> llueve
#> mojado No Sí
#> Mojado 0.70 0.90
#> Seco 0.30 0.10
modelo_jardin$mojado <- tab_3
tab_4 <- xtabs(prob_p ~ piso + mojado, data = p_piso_mojado)
tab_4
#> mojado
#> piso Mojado Seco
#> Muy.resbaladizo 0.30 0.02
#> Resbaladizo 0.60 0.30
#> Normal 0.10 0.68
modelo_jardin$piso <- tab_4
modelo_jardin
#>
#> Bayesian network parameters
#>
#> Parameters of node llueve (multinomial distribution)
#>
#> Conditional probability table:
#>
#> No Sí
#> 0.9 0.1
#>
#> Parameters of node regar (multinomial distribution)
#>
#> Conditional probability table:
#>
#> Apagado Prendido
#> 0.7 0.3
#>
#> Parameters of node mojado (multinomial distribution)
#>
#> Conditional probability table:
#>
#> , , regar = Apagado
#>
#> llueve
#> mojado No Sí
#> Mojado 0.02 0.60
#> Seco 0.98 0.40
#>
#> , , regar = Prendido
#>
#> llueve
#> mojado No Sí
#> Mojado 0.70 0.90
#> Seco 0.30 0.10
#>
#>
#> Parameters of node piso (multinomial distribution)
#>
#> Conditional probability table:
#>
#> mojado
#> piso Mojado Seco
#> Muy.resbaladizo 0.30 0.02
#> Resbaladizo 0.60 0.30
#> Normal 0.10 0.68Finalmente, para hacer inferencia en la red (es decir, calcular probabilidades dado cierto conocimiento), necesitamos usar un algoritmo eficiente (por ejemplo en SAMIAM o GeNIe). Aquí usamos el paquete gRain. Los query que hacemos son la inferencia, pero también se llaman así en la literatura de modelos gráficos. En este caso, podemos examinar las marginales condicionales a toda la evidencia (información) que tenemos.
Por ejemplo, ¿cómo se ven las marginales cuando sabemos que el piso está muy resbaladizo?
library(gRain)
#> Loading required package: gRbase
#>
#> Attaching package: 'gRbase'
#> The following objects are masked from 'package:bnlearn':
#>
#> ancestors, children, parents
#> The following object is masked from 'package:igraph':
#>
#> topo_sort
comp_jardin <- compile(as.grain(modelo_jardin))
querygrain(comp_jardin)
#> $llueve
#> llueve
#> No Sí
#> 0.9 0.1
#>
#> $regar
#> regar
#> Apagado Prendido
#> 0.7 0.3
#>
#> $mojado
#> mojado
#> Mojado Seco
#> 0.2706 0.7294
#>
#> $piso
#> piso
#> Muy.resbaladizo Resbaladizo Normal
#> 0.095768 0.381180 0.523052
query_1 <- setEvidence(comp_jardin, nodes = c('piso'),
states = c('Muy.resbaladizo'))
querygrain(query_1)
#> $llueve
#> llueve
#> No Sí
#> 0.7773787 0.2226213
#>
#> $regar
#> regar
#> Apagado Prendido
#> 0.3058224 0.6941776
#>
#> $mojado
#> mojado
#> Mojado Seco
#> 0.8476735 0.1523265Podemos ver que llueve y mojado son independientes (sin condicionar).
query_2 <- setEvidence(comp_jardin, nodes = c('llueve'), states = c('Sí'))
querygrain(query_2)$regar
#> regar
#> Apagado Prendido
#> 0.7 0.3
query_3 <- setEvidence(comp_jardin, nodes = c('llueve'), states = c('No'))
querygrain(query_2)$regar
#> regar
#> Apagado Prendido
#> 0.7 0.3Y ahora vemos la dependencia entre llueve y regar si condicionamos a piso resbaladizo:
query_4 <- setEvidence(comp_jardin, nodes = c('piso', 'regar'),
states = c('Muy.resbaladizo', 'Apagado'))
querygrain(query_4)$llueve
#> llueve
#> No Sí
#> 0.5506692 0.4493308
query_5 <- setEvidence(comp_jardin, nodes = c('piso', 'regar'),
states = c('Muy.resbaladizo','Prendido'))
querygrain(query_5)$llueve
#> llueve
#> No Sí
#> 0.8772563 0.1227437 Abrir esta red en samiam, y
repetir los queries.
Abrir esta red en samiam, y
repetir los queries.
2.2.1 Independencia condicional y redes bayesianas
Ahora abordamos el segundo enfoque de las redes bayesianas. En este, leemos directamente independencias condicionales a partir de la estructura de la gráfica (es esencialmente equivalente al criterio de factorización).
Independencias condicionales locales
Una distribución de probabilidad (es decir, se factoriza en ) si y sólo si para toda variable , es condicionalmente independiente de cualquier variable que no sea su padre o descendiente dados los padres . Es decir para cualquier que no sea descendiente o padre de . Otra manera de decir esto es que dados los padres, un nodo sólo puede transmitir información probabilística a sus descendientes y a ningún otro nodo.
Por ejemplo, en la siguiente gráfica, el nodo rojo, dado los nodos azules, es condicionalmente independiente de los nodos grises:
gr <- graph(c(1, 4, 2, 5, 3, 5, 4, 6, 5, 6, 7, 8, 6, 8, 8, 9, 8, 10))
plot(gr,
vertex.size = 20,
vertex.color = c(rep('gray80', 3), rep('blue', 2), 'red', 'gray80', 'salmon',
'salmon', 'salmon'),
vertex.label.cex = 1.2, vertex.label.color = 'gray50', vertex.frame.color = NA,
asp = 0.7, edge.arrow.size = 1)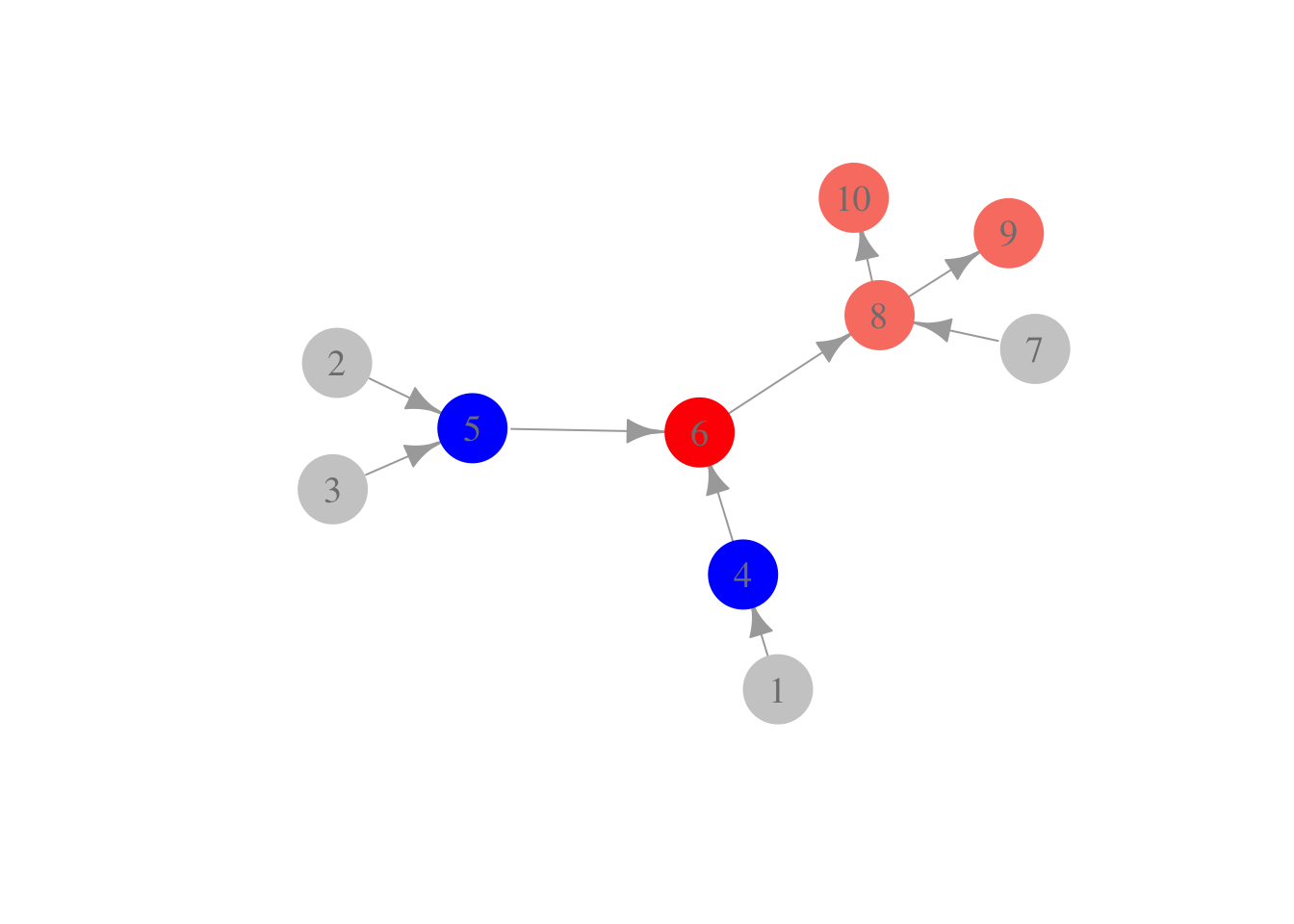
2.2.1.1 Discusión de demostración.
Supongamos que las independencias locales se satisfacen según el enunciado anterior. Si tomamos las variables según el orden topológico de , dado por , entonces por la regla del producto:
Ahora, nótese que 1) para cada , ninguna de las variables es descendiente de y 2) que está contenido en . Por lo tanto, por el supuesto de las independencias locales, vemos que y así hemos demostrado que se factoriza en .
El otro sentido de la demostración es más difícil, veamos un ejemplo. En la siguiente gráfica, describimos una factorización para la conjunta de varias variables: inteligencia de un alumno, dificultad del curso, calificación obtenida en el curso, calificación obtenida en el examen GRE y si el alumno recibe o no una carta de recomendación de su profesor:
library(igraph)
gr <- graph( c(1,3,2,3,2,4,3,5) )
plot(gr,
vertex.label = c('Dificultad','Inteligencia','Calificación','GRE',
'Recomendación'),
layout = matrix(c(-1,2,1,2,0,1,2,1,0,0), byrow = TRUE, ncol = 2),
vertex.size = 20, vertex.color = 'salmon', vertex.label.cex = 1.2,
vertex.label.color = 'gray40', vertex.frame.color = NA, asp = 0.5,
edge.arrow.size = 1)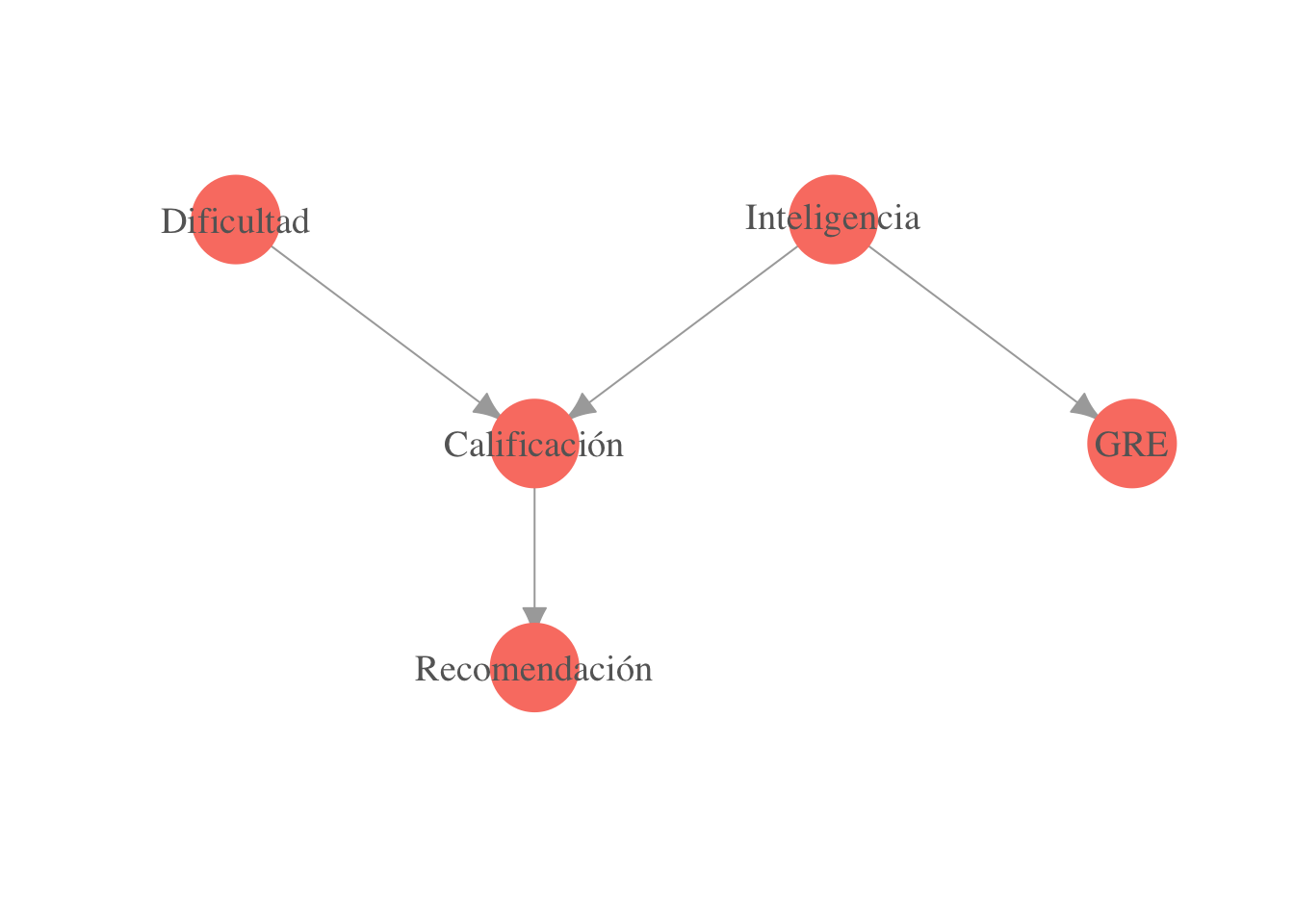
La conjunta se factoriza como
Queremos demostrar que dada la inteligencia, la calificación del GRE es condicionalmente independiente del resto de las variables (pues el resto no son ni padres ni descendientes de GRE), es decir, busamos demostrar que
Comenzamos por la factorización de arriba: Necesitamos calcular Así que comenzamos con la factorización y sumamos sobre para obtener y dividiendo obtenemos que que era lo que queríamos demostrar.
De acuerdo a la gráfica, la calificación en el GRE es independiente de la dificultad una vez que conocemos la inteligencia, es decir , veamos la factorización. Usando el teorema de Bayes podemos calcular la densidad condicional como,
Ahora, comencemos calculando la densidad marginal :
Calculemos ahora el denominador en la regla de Bayes,
Por lo tanto, la densidad condicional es
esto es, la calificación es independiente de la dificultad condicional a la
inteligencia del alumno.
 Repetir para .
Repetir para .
Este último resultado explica cuáles son las independencias condicionales necesarias y suficientes para que una distribución se factorice según la gráfica . Ahora la pregunta que queremos resolver es: ¿hay otras independencias condicionales representadas en la gráfica? Buscamos independencias condicionales no locales. La respuesta es sí, pero necesitamos conceptos adicionales a los que hemos visto hasta ahora (d-separación).
Ejemplo. Antes de continuar, podemos ver un ejemplo de independencias no locales implicadas por la estructura gráfica. Si tenemos:
es fácil ver que es independiente de , dada , aunque esta independencia no es de la forma del resultado anterior, pues no estamos condicionando a los padres de ningún vértice.
2.2.2 Flujo de información probabilística
En esta parte entenderemos primero como se comunica localmente la información probabilística a lo largo de los nodos cuando tenemos información acerca de alguno de ellos. Utilizaremos las factorizaciones implicadas por las gráficas asociadas.
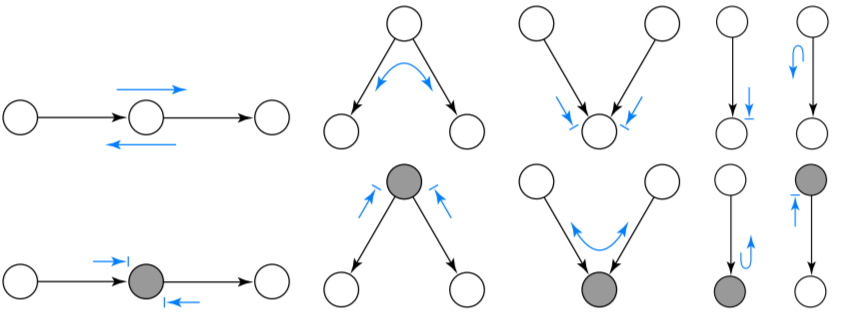
¿En cuáles de los siguientes casos información sobre puede potencialmente cambiar la distribución sobre ?
- Razonamiento causal:
Si no tenemos información acerca de , y pueden estar asociadas. En este caso tenemos , de forma que, haciendo un cálculo simple: Como siempre es cierto que , tenemos donde vemos que cuando cambia , puede cambiar también .
En el ejemplo , si alguien es más joven, entonces es más probable que sea arriesgado, y esto hace más probable que tenga un accidente.
Si sabemos el valor de , sin embargo, no nos da información de . En este caso tenemos , como está fija tenemos que , donde y son funciones fijas. Como la conjunta se factoriza, y son independientes dada .
En nuestro ejemplo, si conociemos la aversión al riesgo, la edad del asegurado no da información adicional acerca de la probabilidad de tener un accidente.
- Razonamiento evidencial:
Si no sabemos acerca de , sí, por un argumento similar al del inciso anterior. Es un argumento de probabilidad inversa en . Si alguien tuvo un accidente, entonces es más probable que sea arriesgado, y por tanto es más probable que sea joven.
Si sabemos el valor que toma , entonces no puede influenciar a , por un argumento similar.
- Razonamiento de causa común: .
Sí, pues en este caso: Sumando sobre tenemos así que
En el ejemplo podríamos tener . Una persona que lleva mucha tiempo manejando es más probablemente mayor, lo cual hace más probable que sea aversa al riesgo.
No. Si conocemos el valor de , entonces y son condicionalmente independientes, pues , donde vemos que una vez que está dada la y no interactuán (están en factores distintos).
- Razonamiento intercausal: Colisionador o estructura-v: .
Si no tenemos información acerca de , no. Esto es porque tenemos de donde vemos que la conjunta de y satisface (sumando sobre ).
Podríamos tener que . Que alguien vaya por una calle en mal estado no cambia las probabilidades de ser un mal conductor (en nuestro modelo).
Si sabemos el valor de , sí conocimiento de puede cambiar probabilidades de . Como tenemos el término (z está fijo) puede incluir interacciones entre y .
En nuestro ejemplo, si sabemos que hubo un accidente, las condiciones de la calle si nos da información acerca de la calidad del conductor: por ejemplo, si la calle está en buen estado, se hace más probable que se trate de un conductor malo.
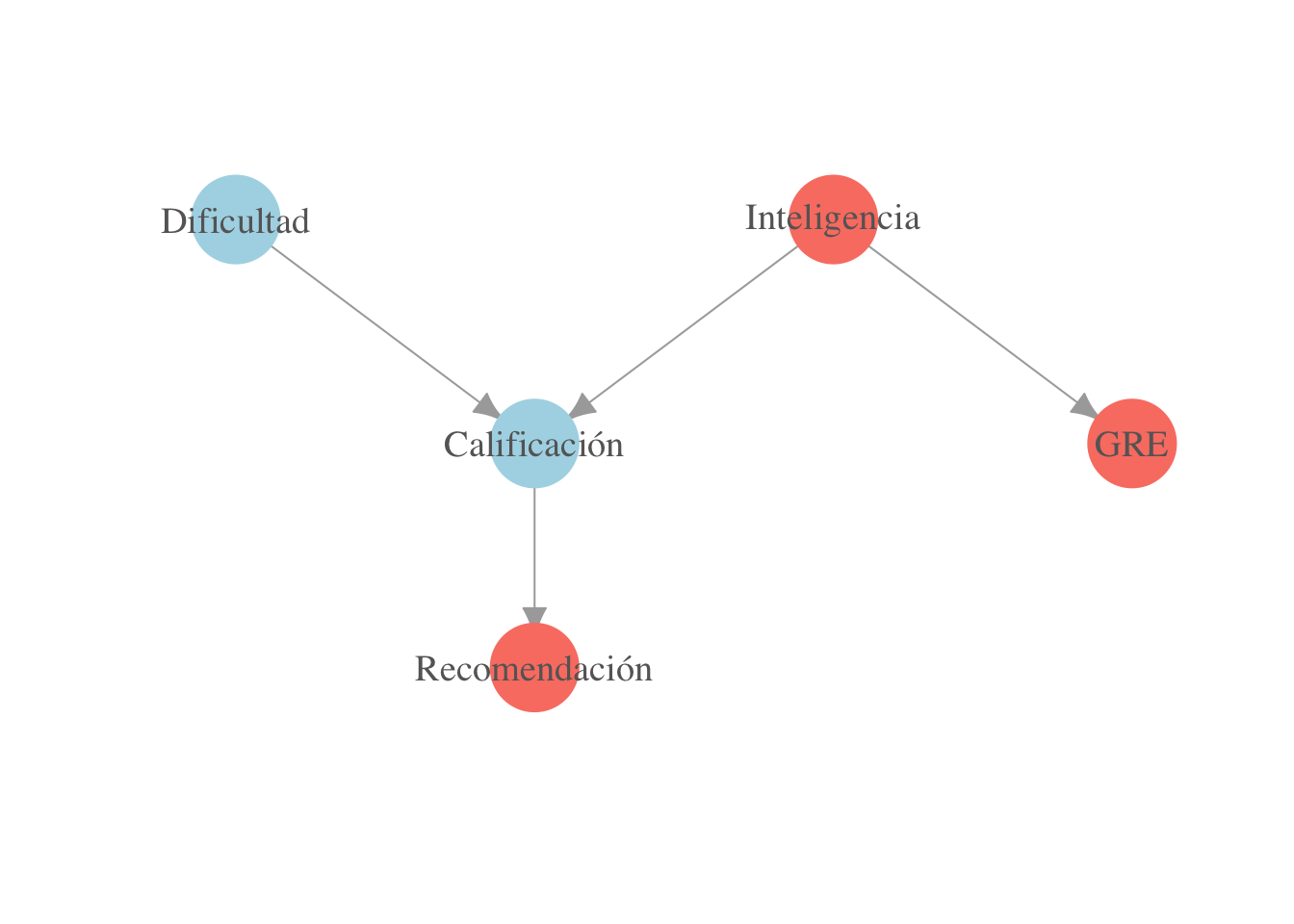
Si sabemos que la clase es difícil y que el estudiante obtuvo 6, ¿como cambia la probabilidad posterior de inteligencia alta? a) sube b) baja c) no cambia d) No se puede saber?
2.2.2.1 Caminos: pelota de Bayes
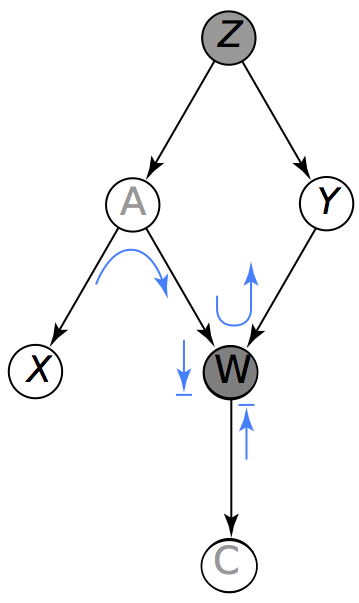
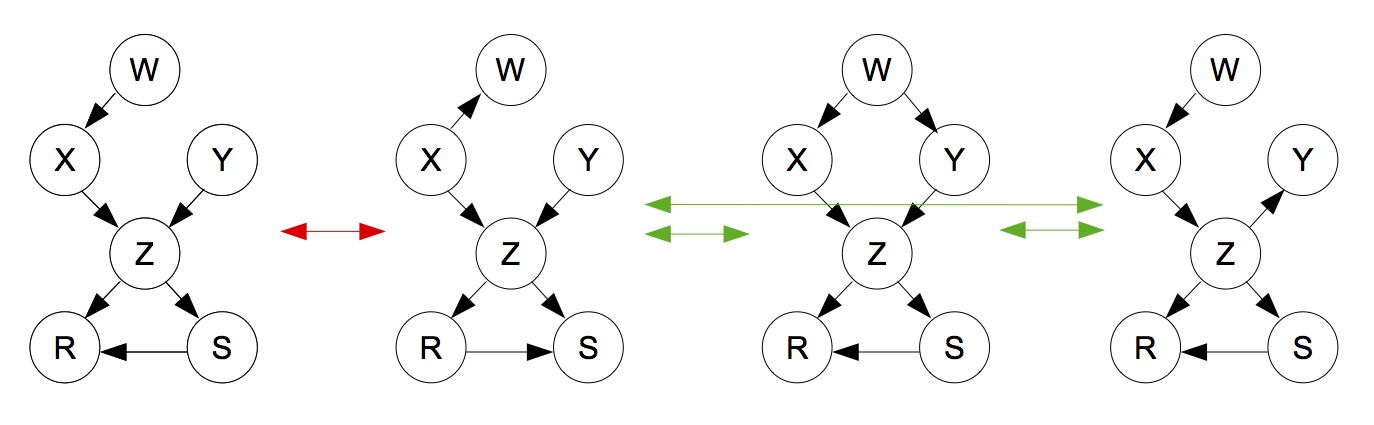
Un camino (no dirigido) esta activo si una pelota de Bayes que viaja a través del camino NO se topa con un símbolo de bloqueo (->|). En los esquemas los nodos sombreados indican que se tiene información de esas variables (ya no son aleatorios).
En la figura de la izquierda (abajo) notamos que (siguiendo las reglas de la pelota de Bayes) la pelota no puede llegar del nodo al nodo , esto es no existe un camino activo que conecte y . Por otra parte, la figura del lado derecho muestra que al condicionar en el conjunto se activa un camino que permite que la pelota de Bayes viaje de a .
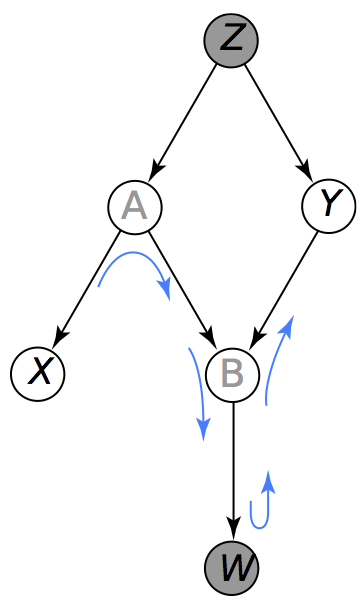
Ahora veamos alegbráicamente que si condicionamos únicamente a , entonces , esto es lo que vemos en la figura de la izquierda. Para esto escribamos la densidad conjunta: Y la utilizamos para obtener la densidad marginal : donde y . Por lo tanto .
 Utilizando la gráfica del lado
derecho demuestra algebráicamente que dados , no es necesariamente
independiente de .
Utilizando la gráfica del lado
derecho demuestra algebráicamente que dados , no es necesariamente
independiente de .
2.2.3 Flujo de probabilidad y d-Separación
De la discusión anterior, definimos caminos activos en una gráfica los que, dada cierta evidencia , pueden potencialmente transmitir información probabilística.
Sea un camino no dirigido en una gráfica . Decimos que el camino es activo dada evidencia si:
Todos los colisionadores en el camino están o tienen un descendiente en .
- Ningún otro vértice de el camino está en .
Un caso adicional interesante es cuando los descendiente de un colisionador activan un camino.
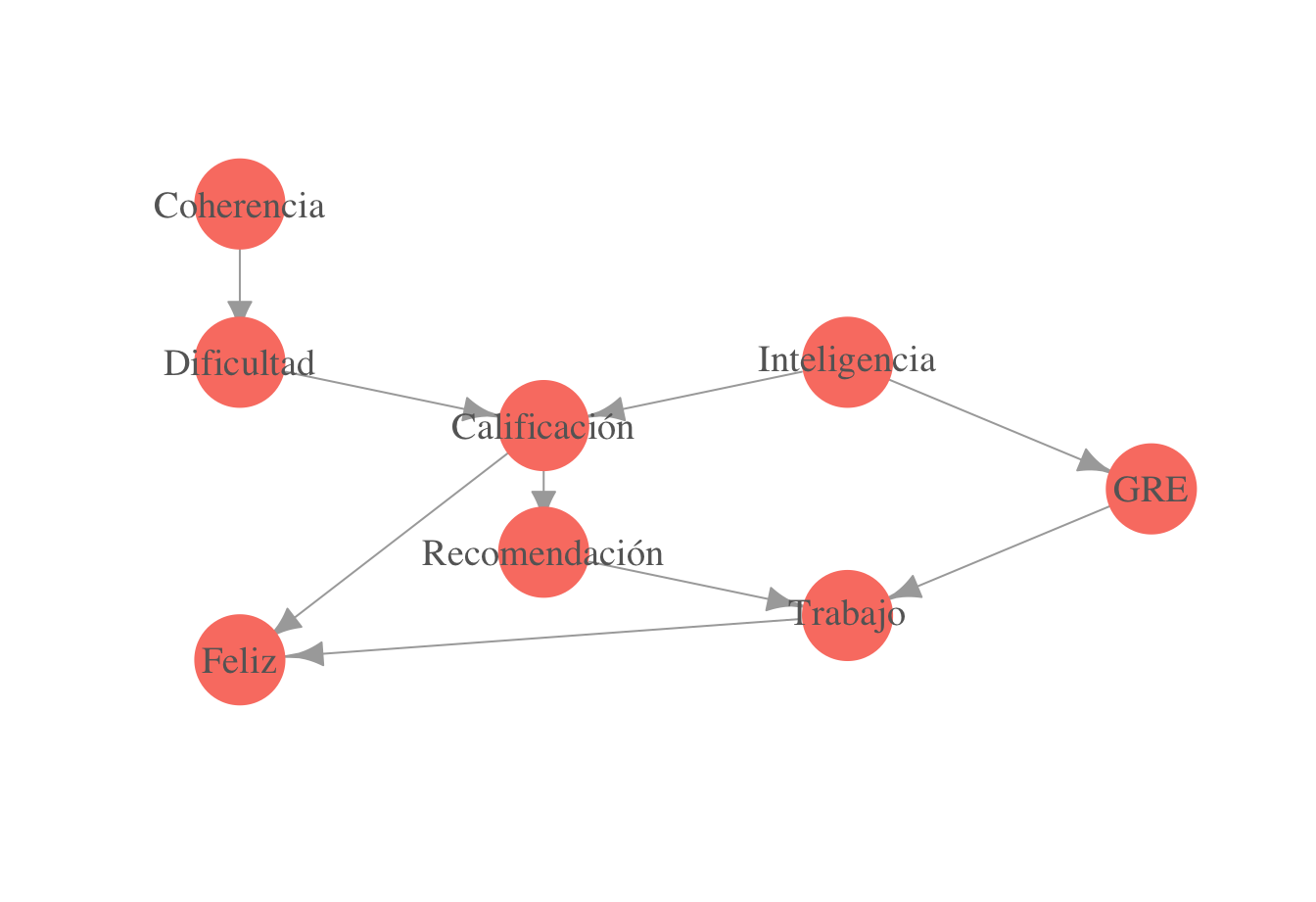
- ¿Cuáles de los siguientes son caminos activos si observamos Calificación?
Volviendo al ejemplo anterior

Algebráicamente: La distribución conjunta se factoriza como: Por lo que la marginal se obtiene de la siguiente manera:
Notamos que y interactúan a través de y , por lo que no es posible encontrar dos funciones , , tales que y concluímos que .
Sean y vértices distintos y un conjunto de vértices que no contiene a o . Decimos que y están d-separados dada si no existen caminos activos dada entre y .
Es decir, la -separación desaparece cuando hay información condicionada en colisionadores o descendientes de colisionadores.
Este concepto de -separación es precisamente el que funciona para encontrar todas las independencias condicionales:
Supongamos que se factoriza sobre . Sean , y conjuntos disjuntos de vértices de . Si y están -separados por entonces bajo .
2.2.3.1 Discusión
El resultado anterior no caracteriza la independencia condicional de una distribución por una razón simple, que podemos entender como sigue: si agregamos aristas a una gráfica sobre la que se factoriza , entonces se factoriza también sobre la nueva gráfica . Esto reduce el número de independencias de que representa .
Un ejemplo trivial son dos variables aleatorias independientes y bajo . claramente se factoriza en , pero de esta gráfica no se puede leer la independencia de y .
¿Qué es lo malo de esto? En primer lugar, si usamos en lugar de , no reducimos la complejidad del modelo al usar las independencias condicionales gráficas que desaparecen al agregar aristas. En segundo lugar, la independencia condicional no mostrada en la gráfica es más difícil de descubrir: tendríamos que ver directamente la conjunta particular de nuestro problema, en lugar de leerla directamente de la gráfica.
Finalmente, estos argumentos también sugieren que quisiéramos encontrar mapeos que no sólo sean mínimos (no se pueden eliminar aristas), sino también perfectos en el sentido de que representan exactamente las independencias condicionales. Veremos estos temas más adelante.
Algo que sí podemos establecer es cómo se comporta la familia de distribuciones que se factorizan sobre una gráfica :
Sea una DAG. Si y no están -separadas en , entonces existe alguna distribución (que se factoriza sobre ) tal que y no son independientes bajo .
Para que existan independencias que no están asociadas a -separación los parámetros deben tomar valores paticulares. Este conjunto de valores es relativamente chico en el espacio de parámetros (son superficies), por lo tanto podemos hacer más fuerte este resultado:
Sea una DAG. Excepto en un conjunto de “medida cero” en el espacio de distribuciones que se factorizan sobre , tenemos que -separación es equivalente a independencia condicional. Es decir, -separación caracteriza precisamente las independencias condicionales de cada , excepto para un conjunto relativamente chico de .
2.2.4 Equivalencia Markoviana
En esta parte trataremos el problema de la unicidad de la representación gráfica dada un conjunto de independencias condicionales. La respuesta corta es que las representaciones no son únicas, pues algunas flechas pueden reorientarse sin que haya cambios en términos de la conjunta representada.
Decimos que dos gráficas y son Markov equivalentes cuando el conjunto de independencias implicadas de ambas es el mismo. Otra manera de decir esto, es que ambas gráficas tienen exactamente la misma estructura de separación.
La equivalencia Markoviana limita nuestra capacidad de inferir la dirección de las flechas únicamente de las probabilidades, esto implica que dos gráficas Markov equivalentes no se pueden distinguir usando solamente una base de datos. Por ejemplo, en la siguiente gráfica, cambiar la dirección del arco que une y genera una gráfica Markov equivalente, esto es, la dirección del arco que une a y no se puede inferir de información probabilística.
library(igraph)
gr <- graph( c(1,2,1,3,2,4,3,4,4,5) )
plot(gr, vertex.label=c('X1','X2','X3','X4','X5'),
layout = matrix(c(-0.3,0,0,-0.3,0, 0.3,0.3,0,0.6,0), byrow = TRUE, ncol = 2),
vertex.size = 20, vertex.color = 'salmon', vertex.label.cex = 1.2,
vertex.label.color = 'gray40', vertex.frame.color = NA, asp = 0.5,
edge.arrow.size = 1)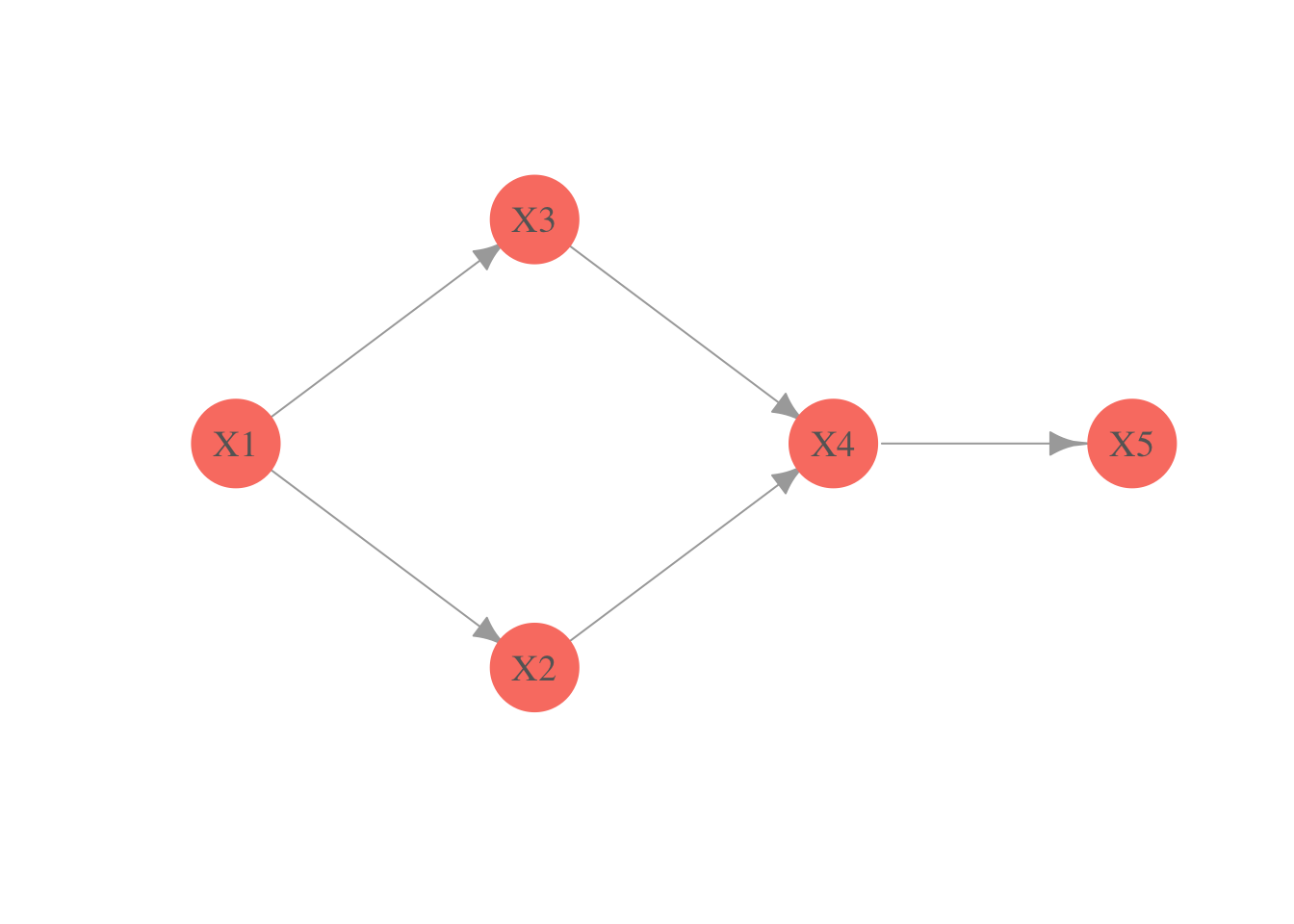
Decimos que un colisionador no está protegido cuando las variables que apuntan a la colisión no tienen vértice entre ellas. Definimos adicionalmente el esqueleto de una GAD como la versión no dirigida de . El siguiente resultado establece que la distribución sólo puede determinar la dirección de las flechas en presencia de un colisionador no protegido:
Dos gráficas y son Markov equivalentes si y sólo si
Sus esqueletos son iguales y
- y tienen los mismos colisionadores no protegidos.
Las equivalencias que señala este teorema son importantes. Por ejemplo, las gráficas y son equivalentes, lo que implica que representan a las mismas distribuciones condicionales. Solamente usando datos (o el modelo), no podemos distinguir estas dos estructuras, sin embargo, puede ser que tengamos información adicional para preferir una sobre otra (por ejemplo, si es una serie de tiempo).
Una estructura que sí podemos identificar de manera dirigida es el colisionador. El resto de las direcciones pueden establecerse por facilidad de interpretación o razones causales.
Regresando a la gráfica anterior, notamos que al revertir el sentido del arco que une a con no se crea ni se destruye ningun colisionador y por tanto la gráfica resultante del cambio de sentido es efectivamente Markov equivalente. Consideremos ahora los arcos dirigidos que unen a con y a con , notamos que no hay manera de revertir la dirección de estos arcos sin crear un nuevo colisionador, esto implica que algunas funciones de probabilidad restringen la dirección de éstas flechas en la gráfica.
En el siguiente ejemplo, mostramos la clase de equivalencia de una red de ejemplo. Ahí vemos cuáles son las aristas que se pueden orientar de distinta manera, y cuáles pertenecen a colisionadores en los cuales las direcciones están identificadas:
library(bnlearn)
grafica.1 <- gs(insurance[c('Age', 'RiskAversion', 'Accident', 'DrivQuality',
'Antilock', 'VehicleYear')], alpha = 0.01)
graphviz.plot(grafica.1)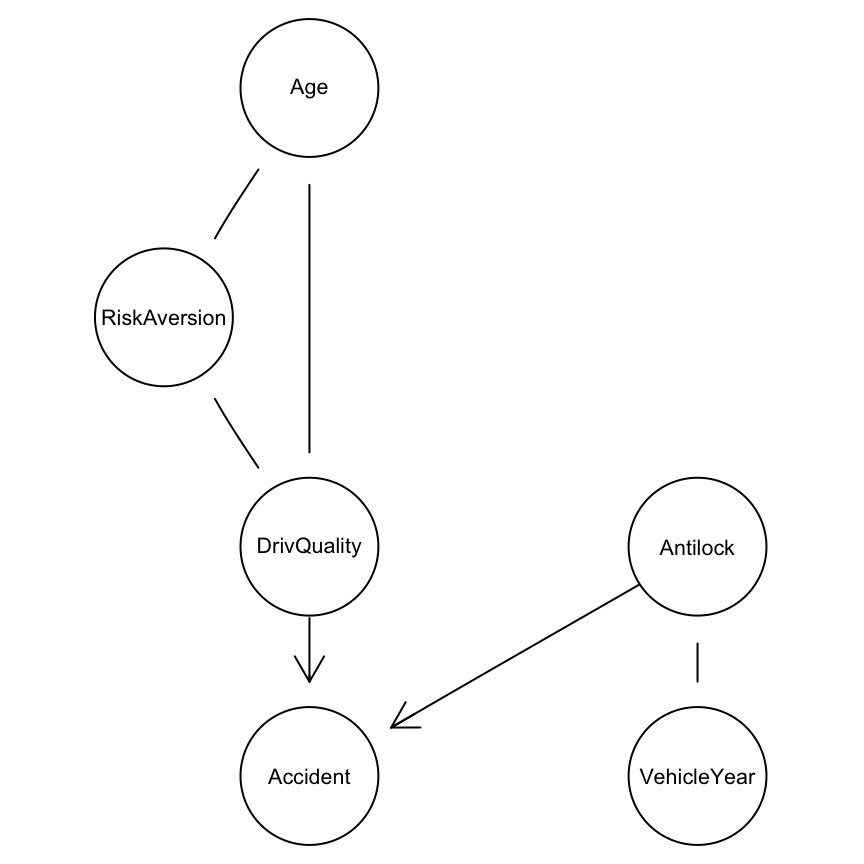
¿Cuáles de las gráficas anteriores son Markov equivalentes?
- 1 y 2
- 1 y 3
- 2 y 4
- 2 y 4
- Ninguna
Resumen
- Dada una gráfica podemos encontrar las as independencias condicionales que
establece, .
- Dada una distribución podemos encontrar las independencias que implica, (en teoría).
- Las independencias condicionales definidas por la red bayesiana son un
subconjunto de las independencias en , esto es .
- Equivalencia Markoviana se expresa como: .