5.3 Métodos de imputación para varias variables
En esta sección explicaremos la imputación para el caso de faltantes en varias variables y la implementación de imputación del paquete mi, para esto utilizamos el ejemplo del artículo Multiple Imputation with Diagnostics (mi) in R de Yu-sUng Su et al.
Imputación multivariada. Un método de imputación directo es ajustar un modelo multivariado a todas las variables con datos faltantes. La dificultad de este método es que requiere mucho esfuerzo llegar a un modelo razonable de regresión multivariado, es por ello que en la práctica se suelen usar modelos estándar como el normal multivariado o una distribución multinomial para datos discretos. Las calidad de estas imputaciones depende del modelo por lo que se necesitan evaluar el ajuste del mismo; sin embargo, es común que la implementación sea una caja negra.
Imputación iterativa. Una manera de generalizar los métodos univariados (cuando solo tengo faltantes en una variable) es aplicarlos iterativamente. Si las variables con datos faltantes son una matriz \(Y=(Y_1,...,Y_K)\) y las variables completamente observadas son X, comenzamos imputando todos los valores de \(Y\) (por ejemplo, seleccionando de los datos observados al azar para cada faltante), y después imputar \(Y_1\) dado \(Y_2,...,Y_K\) y \(X\), imputar \(Y_2\) dado \(Y_1,Y_3,...,Y_K\) y \(X\) donde sustituimos por los valores recien imputados para \(Y_1\) y procedemos de esta manera: imputando con procedimientos al azar hasta alcanzar algún criterio de convergencia.
Ejemplo. Veamos un ejemplo proveniente de la encuesta de indicadores sociales de Nueva York.
wave3 <- read.table("data/sis.csv", header = T, sep = ",")
# No lo hagan!
attach(wave3)
n <- nrow(wave3)
# missing codes: -9: refused/dk to say if you have this source
# -5: you said you had it but refused/dk the amount
# Variables:
# rearn: respondent's earnings
# tearn: spouse's earnings
# ssi: ssi for entire family
# welfare: public assistance for entire family
# charity: income received from charity for entire family
# sex: male=1, female=2
# race of respondent: 1=white, 2=black, 3=hispanic(nonblack), 4=other
# immig: 0 if respondent is U.S. citizen, 1 if not
# educ_r: respondent's education (1=no hs, 2=hs, 3=some coll, 4=college grad)
# DON'T USE primary: -9=missing, 0=spouse, 1=respondent is primary earner
# workmos: primary earner's months worked last year
# workhrs: primary earner's hours/week worked last year
# Creamos algunas variables
white <- ifelse(race == 1, 1, 0)
white[is.na(race)] <- 0
male <- ifelse(sex == 1, 1, 0)
over65 <- ifelse (r_age > 65, 1, 0)
immig[is.na(immig)] <- 0
educ_r[is.na(educ_r)] <- 2.5
# Funciones auxiliares
# Codificar NAs
na.fix <- function(a){
ifelse (a<0 | a==999999, NA, a)
}
is.any <- function (a) {
any.a <- ifelse(a>0, 1, 0)
any.a[is.na(a)] <- 0
return(any.a)
}
earnings <- na.fix(rearn) + na.fix(tearn)
earnings[workmos==0] <- 0
# variables resumen para distintos ingresos
any.ssi <- is.any(ssi)
any.welfare <- is.any(welfare)
any.charity <- is.any(charity)
earnings <- earnings/1000
## Imputación aleatoria simple
random.imp <- function (a){
missing <- is.na(a)
n.missing <- sum(missing)
a.obs <- a[!missing]
imputed <- a
imputed[missing] <- sample (a.obs, n.missing, replace=TRUE)
return (imputed)
}
earnings.imp <- random.imp(earnings)
## Zero coding and topcoding
# Topcoding reduce la sensibilidad del los resultados a los valores más altos
# zero coding se utiliza para ajustar el modelo de regresión únicamente a
# aquellas personas con ingreso positivo
topcode <- function (a, top){
return (ifelse (a>top, top, a))
}
earnings.top <- topcode(earnings, 100)
workhrs.top <- topcode(workhrs, 40)
## Descrpción
# interest: interest of entire family
interest <- na.fix(interest)
# transforming the different sources of income
interest <- interest/1000
## Simple random imputation
interest.imp <- random.imp (interest)
## Imputación iterativa
datos <- data.frame(earnings, interest.imp, male, over65, white, immig,
educ_r, workmos, workhrs.top, any.ssi, any.welfare, any.charity)
str(datos)
impute <- function(a, a.impute){
ifelse(is.na(a), a.impute, a)
}
# número de iteraciones
n.sims <- 10
# Y: earnings, interest
for (s in 1:n.sims){
lm.1 <- lm (earnings ~ interest.imp + male + over65 + white + immig +
educ_r + workmos + workhrs.top + any.ssi + any.welfare + any.charity)
pred.1 <- rnorm(n, predict(lm.1), sigma.hat(lm.1))
earnings.imp <- impute (earnings, pred.1)
lm.2 <- lm (interest ~ earnings.imp + male + over65 + white + immig +
educ_r + workmos + workhrs.top + any.ssi + any.welfare + any.charity)
pred.2 <- rnorm(n, predict(lm.2), sigma.hat(lm.2))
interest.imp <- impute(interest, pred.2)
}Ahora veamos como realizar una imputación usando el paquete mi. Este paquete describe la imputación de datos como un proceso que consta de 4 pasos.
- Preparación
Visualización de patrones de datos faltantes.
Identificación de problemas estructurales en los datos y preprocesamiento de los mismos.
- Imputación
Imputación iterativa con base al modelo condicional.
Revisón del ajuste de los modelos condicionales con el fin de observar si los valores imputados son razonables.
Revisión de convergencia del procedimiento.
- Análisis
Obtención de datos completos.
Combinación (pooling) del análisis de datos completos en múltiples conjuntos de datos imputados.
- Validación
Análisis de sensibilidad.
Validación cruzada.
Revisión de compatibilidad
5.3.1 Ejemplo: Ecuesta de jóvenes de EUA
Seguiremos el ejemplo de la documentación del paquete mi y explicaremos los
pasos de la imputación. Los datos consisten en un extracto (no longitudinal) de
la enucesta nacional de joventud de EUA.
1. Preparación
Comencemos con la visualización de patrones en los datos faltantes. Los patrones de datos faltantes se refieren a la configuración de datos observados y faltantes de una base de datos.
La gráfica del lado izquierdo muestra la matriz con los datos observados y los
faltantes. Esta gráfica puede ser difícil de interpretar, es por ello
que en la figura del lado derecho ordenamos y creamos conglomerados con los
datos, para la visualización usamos el paquete visdat.
library(mi)
library(visdat)
library(gridExtra)
data(nlsyV)
par(mfrow = c(1,2))
vis <- vis_miss(nlsyV)
vis_clust <- vis_miss(nlsyV, cluster = TRUE, sort_miss = TRUE)
grid.arrange(vis, vis_clust, ncol = 2)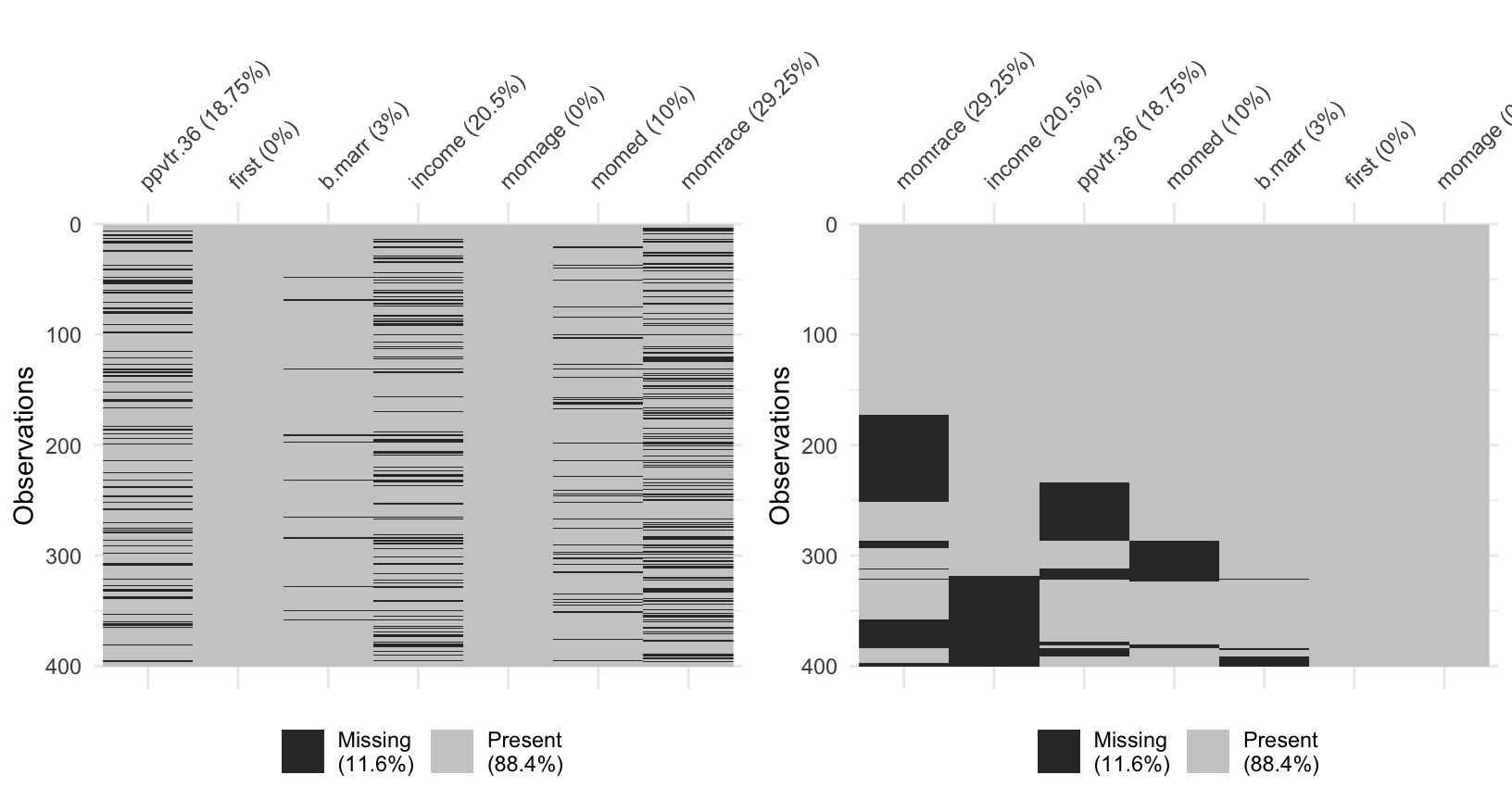
Lo que sigue es usar la instrucción missing_data.frame para crear una clase
similar a data.frame con información que especifica el tipo de dato y de
modelo de imputación que se usará.
mdf <- missing_data.frame(nlsyV)
#> NOTE: In the following pairs of variables, the missingness pattern of the first is a subset of the second.
#> Please verify whether they are in fact logically distinct variables.
#> [,1] [,2]
#> [1,] "b.marr" "income"
show(mdf)
#> Object of class missing_data.frame with 400 observations on 7 variables
#>
#> There are 20 missing data patterns
#>
#> Append '@patterns' to this missing_data.frame to access the corresponding pattern for every observation or perhaps use table()
#>
#> type missing method model
#> ppvtr.36 continuous 75 ppd linear
#> first binary 0 <NA> <NA>
#> b.marr binary 12 ppd logit
#> income continuous 82 ppd linear
#> momage continuous 0 <NA> <NA>
#> momed ordered-categorical 40 ppd ologit
#> momrace ordered-categorical 117 ppd ologit
#>
#> family link transformation
#> ppvtr.36 gaussian identity standardize
#> first <NA> <NA> <NA>
#> b.marr binomial logit <NA>
#> income gaussian identity standardize
#> momage <NA> <NA> standardize
#> momed multinomial logit <NA>
#> momrace multinomial logit <NA>También podemos realizar cambios en mdf usando la función change().
mdf <- change(mdf, y = c("income", "momrace"), what = "type",
to = c("non", "un"))
#> NOTE: In the following pairs of variables, the missingness pattern of the first is a subset of the second.
#> Please verify whether they are in fact logically distinct variables.
#> [,1] [,2]
#> [1,] "b.marr" "income"2. Imputación
Una vez que preparamos todo, la imputación es sencilla; sin embargo, se debe verificar el ajuste de los modelos y la convergencia.
imp <- mi(mdf, n.iter = 20, n.chains = 4, verbose = FALSE)
show(imp)
#> Object of class mi with 4 chains, each with 20 iterations.
#> Each chain is the evolution of an object of missing_data.frame class with 400 observations on 7 variables.Si el ajuste de los modelos de imputación es malo es poco probable que
imputemos valores razonables. Podemos revisar el ajuste usando las siguientes
gráficas que regresa la función plot(), para las primeras tres cadenas
tenemos:
Histogramas de los observados (azúl) e imputados (rojo).
Un diagrama de dispersión que grafica los valores observados contra los valores depredicción, además se agrega una curva loess.
Binned residuals que grafica el promedio de los residuales, en bins, contra los valores esperados.
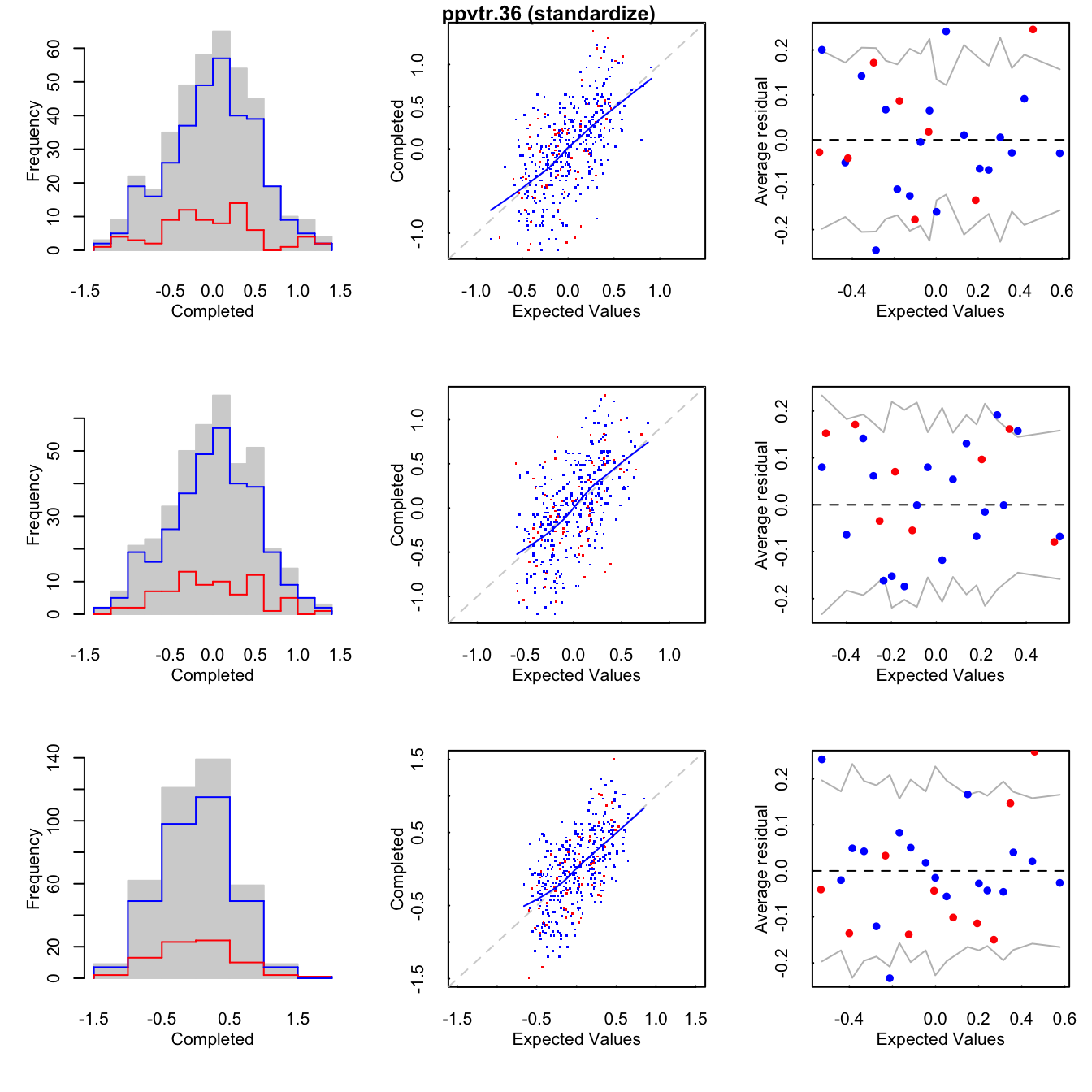
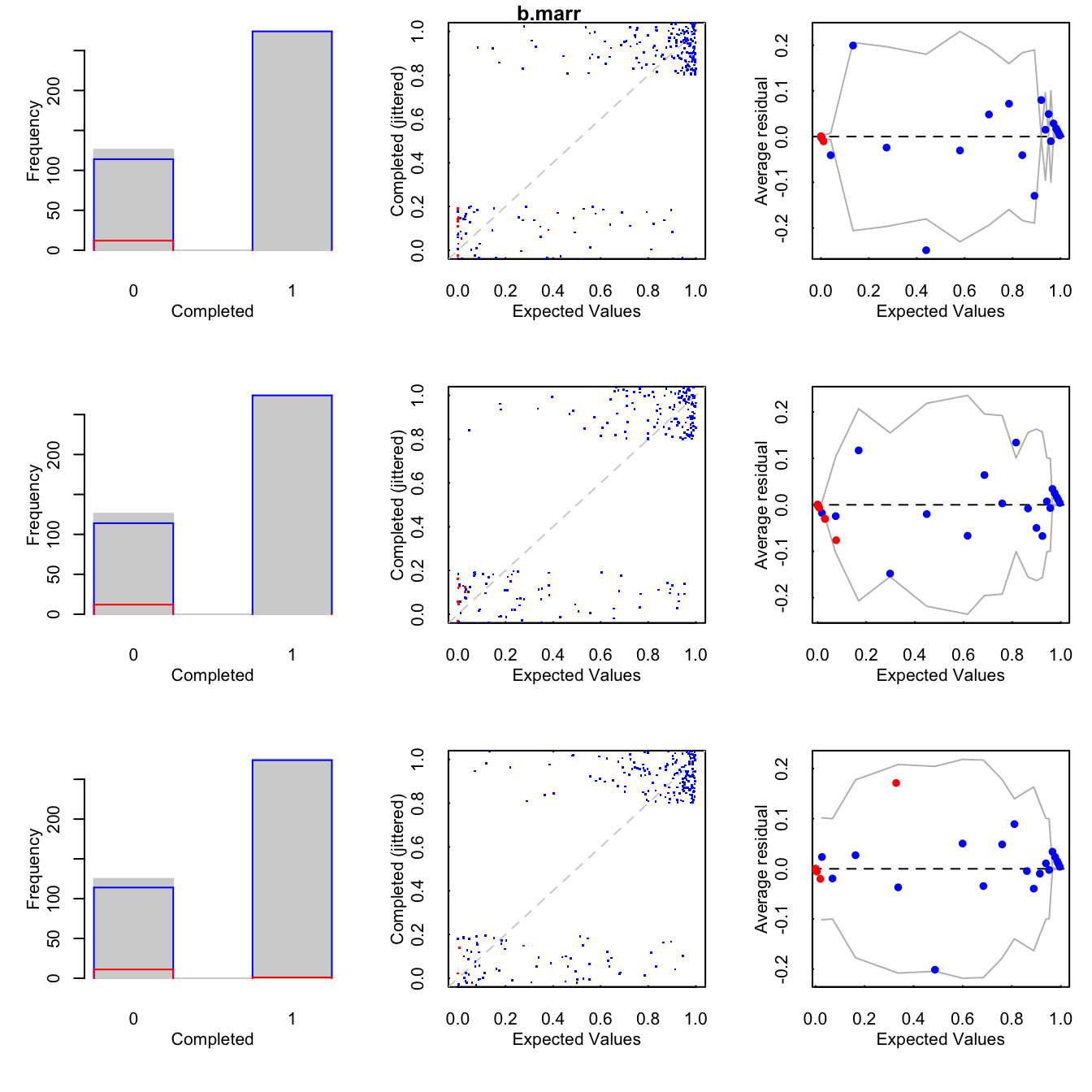
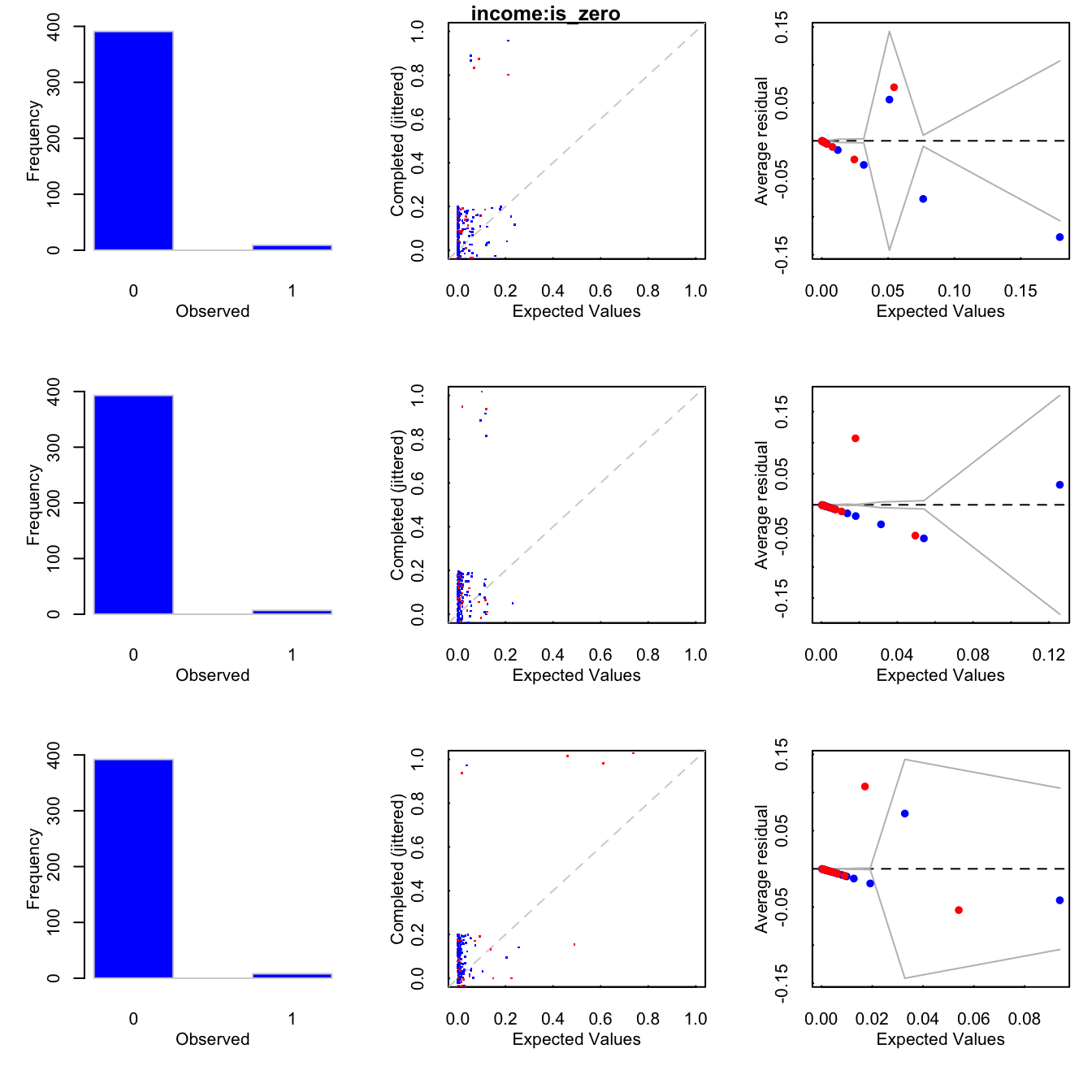
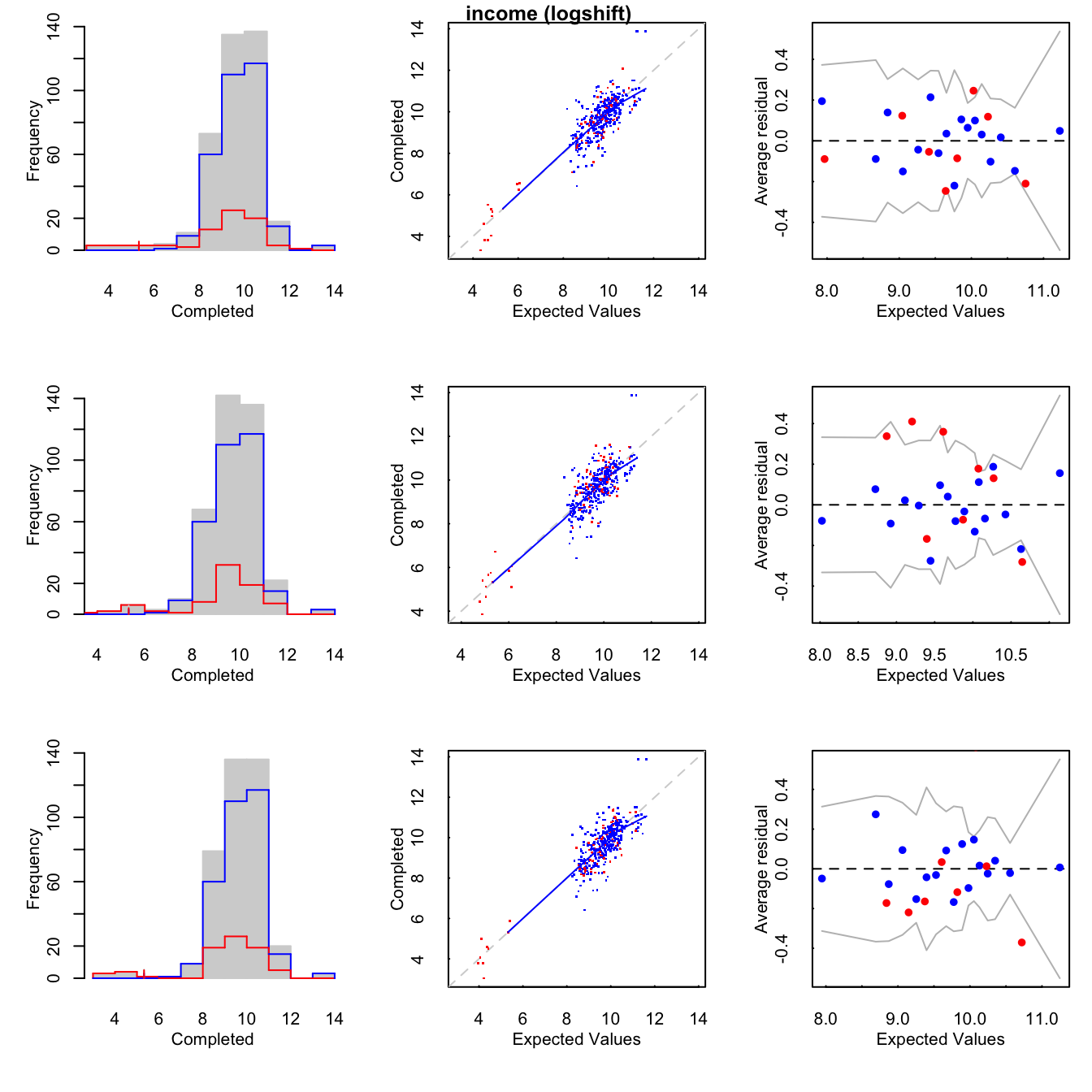
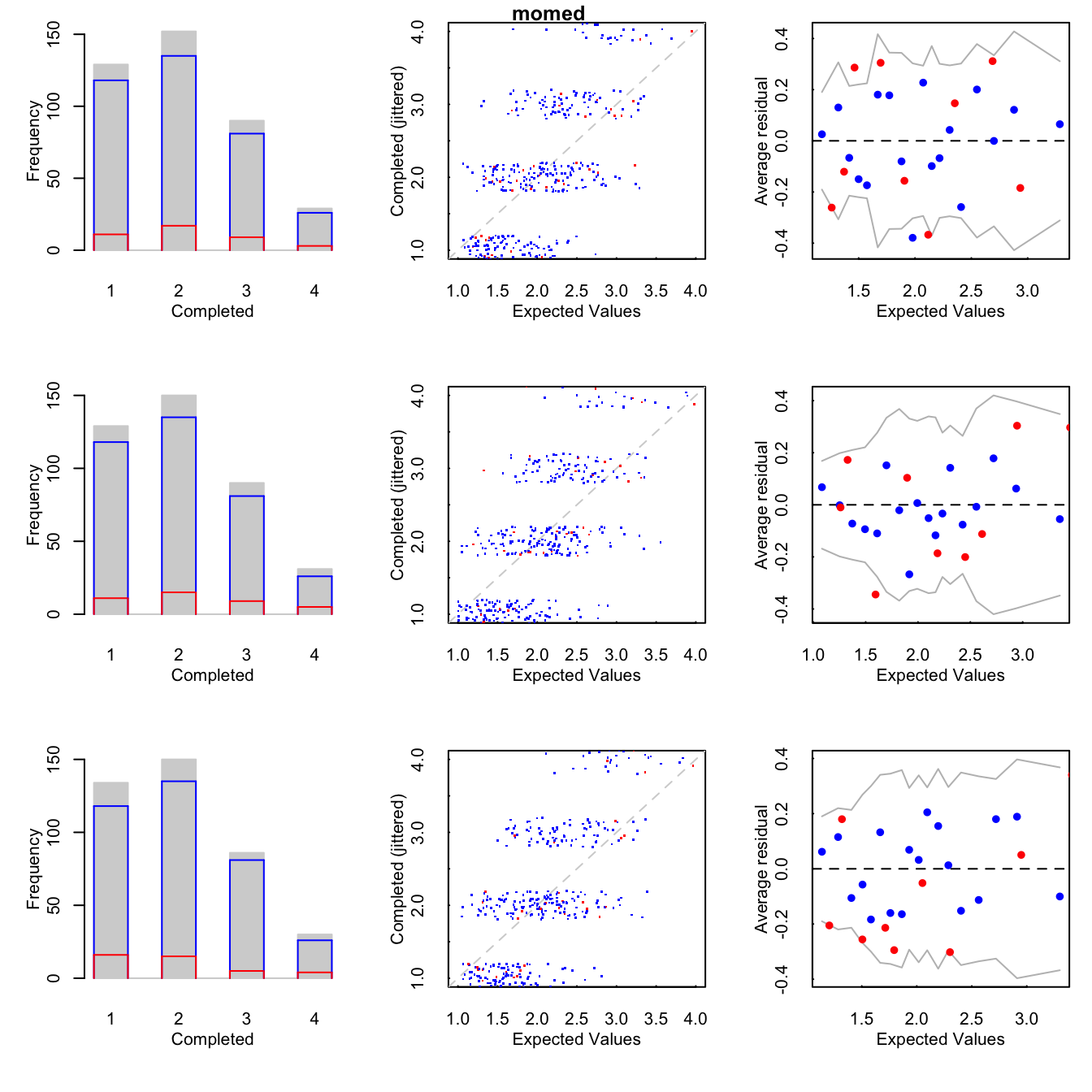
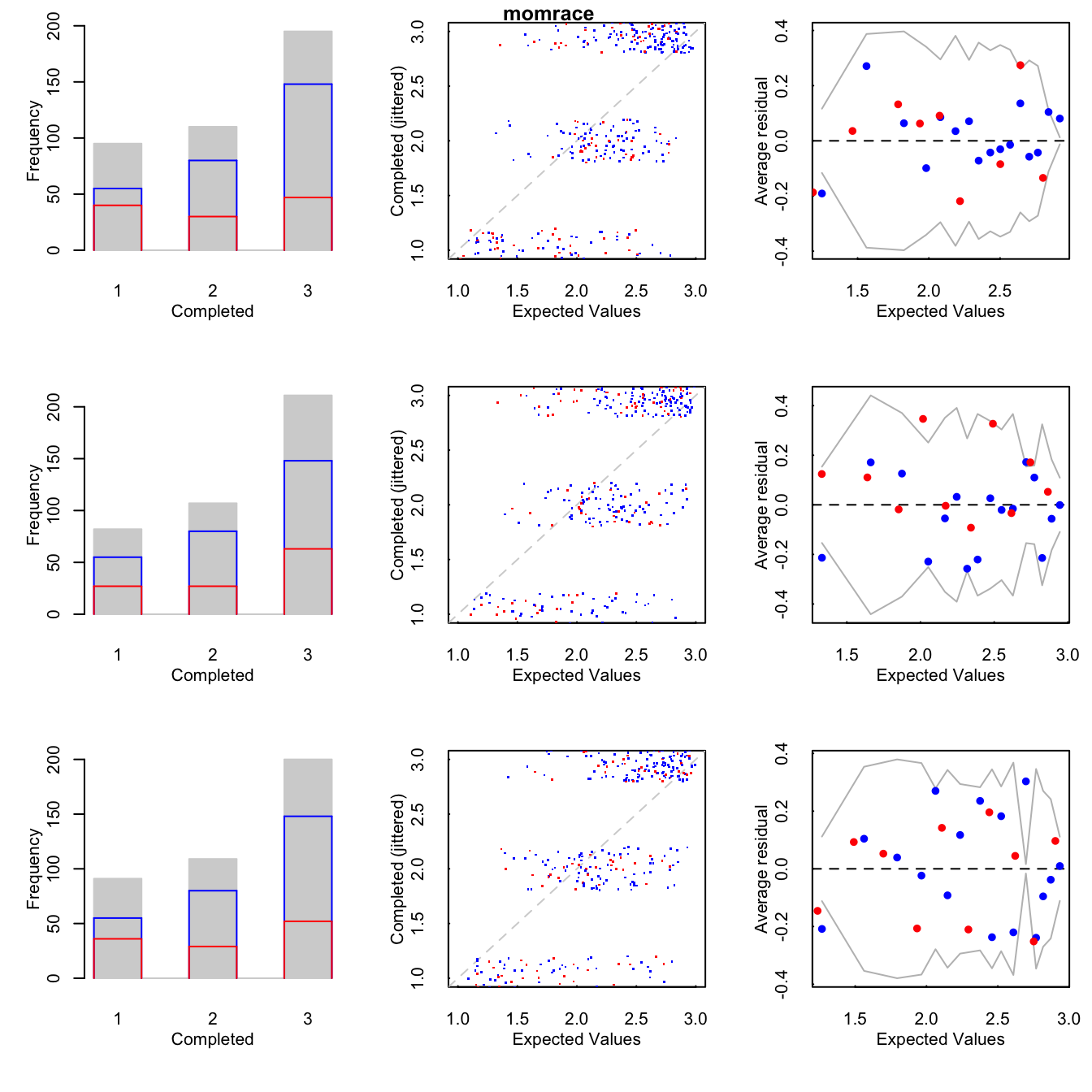
Las gráficas también nos pueden ayudar a detectar si no se cumple el supuesto MAR, pues podemos comparar los valores observados y los valores imputados.
Notemos que el gráfico de binned residuals muestra que se puede mejorar el modelo de imputación para income pues hay muchos residuales que caen por fuera de las bandas de 95% de error.
En cuanto a convergencia mi calcula la media y desviación estándar de cada
variable en distintas cadenas, queremos que la media de cada variable coincida
a lo largo de las cadenas.
round(mipply(imp, mean, to.matrix = TRUE), 3)
#> chain:1 chain:2 chain:3 chain:4
#> ppvtr.36 -0.007 -0.005 -0.004 -0.011
#> first 1.435 1.435 1.435 1.435
#> b.marr 1.685 1.685 1.688 1.685
#> income 9.492 9.558 9.528 9.561
#> momage 0.000 0.000 0.000 0.000
#> momed 2.047 2.058 2.030 2.058
#> momrace 2.250 2.322 2.272 2.255
#> missing_ppvtr.36 0.188 0.188 0.188 0.188
#> missing_b.marr 0.030 0.030 0.030 0.030
#> missing_income 0.205 0.205 0.205 0.205
#> missing_momed 0.100 0.100 0.100 0.100
#> missing_momrace 0.292 0.292 0.292 0.292Más aún tenemos una medida de convergencia, se considera que la imputación ha convergido si \(\hat{R} < 1.1\) para todos los parámetros.
Rhats(imp)
#> mean_ppvtr.36 mean_b.marr mean_income mean_momed mean_momrace
#> 0.9846084 0.9830807 1.0251987 1.0603464 0.9975480
#> sd_ppvtr.36 sd_b.marr sd_income sd_momed sd_momrace
#> 0.9997941 0.9837253 1.1545309 1.0343478 0.9878776Si no se ha logrado convergencia podemos continuar las iteraciones sobre el objeto mi anterior:
3. Combinación de inferencias (Rubin 1987)
En el proceso anterior realizamos 4 cadenas de imputaciones, esto es, tenemos 4 bases de datos con datos imputados. Podemos extraer las bases de datos con los datos imputados para hacer análisis.
O podemos extraer únicamente uno.
imp_dat <- complete(imp, m = 1)
head(imp_dat)
#> ppvtr.36 first b.marr income momage momed momrace missing_ppvtr.36
#> 1 105.00000 1 1 21446 20 2 3 FALSE
#> 2 91.00000 1 1 12125 22 2 3 FALSE
#> 3 89.00000 0 1 13560 22 2 1 FALSE
#> 4 85.00000 0 1 24500 28 3 2 FALSE
#> 5 66.00000 0 0 3304 20 1 2 FALSE
#> 6 72.71589 0 0 5832 27 2 3 TRUE
#> missing_b.marr missing_income missing_momed missing_momrace
#> 1 FALSE FALSE FALSE FALSE
#> 2 FALSE FALSE FALSE FALSE
#> 3 FALSE FALSE FALSE FALSE
#> 4 FALSE FALSE FALSE TRUE
#> 5 FALSE FALSE FALSE TRUE
#> 6 FALSE FALSE FALSE TRUEAl hacer análisis, en lugar de reemplazar cada valor faltante con un valor imputado de manera aleatoria, tiene sentido reemplazar cada valor faltante con varios valores imputados que reflejen nuestra incertidumbre acerca del modelo de imputación.
Por ejemplo, si imputamos usando un modelo de regresión queremos reflejar no solamente la variación muestral (propia de imputación aleatoria), sino también la incertidumbre de los coeficientes de regresión del modelo. Si modelamos los coeficientes mismos, podemos obtener un nuevo conjunto de imputaciones para cada conjunto simulado de la distribución de coeficientes.
Esta es la idea detrás de imputación multiple, se generean varios valores imputados para cada valor faltante, cada uno es la predicción de un modelo ligeramente diferente y que además refleja variabilidad muestral. ¿Cómo analizamos estos datos? La idea es usar cada conjunto de datos imputados (junto con los observados) para crear conjuntos de datos completos. Dentro de cada conjunto de datos completos podemos llevar a cabo un análisis estándar.
Por ejemplo, supongamos que queremos hacer inferencia acerca de un coeficiente de regresión \(\beta\), obtenemos estimaciones \(\hat{\beta}_m\) usando cada uno de los M conjuntos de datos, y obtenemos también errores estándar \(s_1,...,s_M\). Para obtener una estimación puntual usamos la media de las \(M\) estimaciones: \[\hat{\beta}=\frac{1}{M}\sum_{m}\hat{\beta}_m\]
En cuanto al error estándar, no es tan sencillo como la media. Recordemos que los errores estándar provenientes de imputaciones múltiples tienen dos fuentes de variación: el error estándar que hubiese resultado si los datos fueran completos y el error muestral adicional proveniente de los datos faltantes. Es así que las fórmulas de varianza consisten de un término correspondiente a variación dentro (Within) y otro entre (Between):
\[V_{\beta} = W + (1+\frac{1}{M})B\]
La varianza dentro es el promedio de las varianzas:
\[W=\frac{1}{M}\sum_{m}s_m^2\]
y estima la variabilidad que hubiera resultado si no hubiera datos faltantes. Por otra parte, como hemos discutido, los valores faltantes deben aumentar los errores estándar, es así que surge el término de varianza Between.
\[B=\frac{1}{M-1}\sum_{m}(\hat{\beta}_m-\hat{\beta})^2\]
que representa la variación adicional debida a las fluctuaciones entre \(\hat{\beta}_m\) provenientes de los diferentes valores imputados.
Para hacer este proceso en mi haríamos:
fit <- pool(ppvtr.36 ~ first + b.marr + income + momage + momed + momrace, imp)
display(fit)
#> bayesglm(formula = ppvtr.36 ~ first + b.marr + income + momage +
#> momed + momrace, data = imp)
#> coef.est coef.se
#> (Intercept) 81.62 8.82
#> first1 3.43 1.88
#> b.marr1 5.39 2.63
#> income 0.00 0.00
#> momage -0.15 0.35
#> momed.L 11.73 2.72
#> momed.Q 1.09 2.08
#> momed.C -0.80 1.97
#> momrace2 -5.41 2.90
#> momrace3 13.16 2.81
#> n = 390, k = 10
#> residual deviance = 93772.1, null deviance = 146444.1 (difference = 52672.0)
#> overdispersion parameter = 240.4
#> residual sd is sqrt(overdispersion) = 15.514. Validación
Análisis de sensibilidad: Podemos evaluar la sensibilidad de los resultados de los análisis agregados ante cambios en la especificación de los modelos dentro del conjunto de modelos posibles de acuerdo a la evaluación gráfica.
Validación cruzada. Podemos evaluar el supuesto MAR, creando datos faltantes de los datos imputados usando los mecansimos de faltantes que suponemos. Reimputamos y comparamos.
5.3.2 Otros aspectos a tomar en cuenta
Imputación de datos colineales. El paquete mi tiene estrategias para dos casos: correlación perfecta y restricciones aditivas.
Correlación perfecta. En muchos datos una variable aparece más de una vez, en distintas escalas. Por ejemplo, podríamos tener PIB per cápita en pesos y en miles de pesos. En este caso, si el patrón de faltantes es el mismo en ambas variables, mi() incluirá sólo una de las variables duplicadas como parte del proceso iterativo y después copiará los valores a la variable no imputada.
Restricciones aditivas.
5.3.3 Recursos adicionales
Statistical Analysis with Missing Data Little, Rubin.
Data Analysis Using Regression and Multilevel/Hierarchical Models cap. 25, Gelman, Hill.
A multivariate technique for multiply imputing missing values using a sequence of regression models Van Hoewyk, Lepkowski, Solenberger y Raghunathan.
Applied Missing Data Analysis, Enders.