7.1 Motivación

Ejemplo: serie de terremotos. La siguiente serie cuenta el número de temblores de magnitud 7 o más en el mundo, desde 1900 a 2006 (Hidden Markov Models for Time Series, de Zucchini y MacDonald):

terremotos <- data.frame(num = c(13,14,8,10,16,26,32,27,18,32,36,24,22,23,22,18,
  25,21,21,14,8,11,14,23,18,17,19,20,22,19,13,26,13,14,22,24,21,22,26,21,23,24,
  27,41,31,27,35,26,28,36,39,21,17,22,17,19,15,34,10,15,22,18,15,20,15,22,19,16,
  30,27,29,23,20,16,21,21,25,16,18,15,18,14,10,15,8,15,6,11,8,7,18,16,13,12,13,
  20,15,16,12,18,15,16,13,15,16,11,11), anio = 1900:2006)
ggplot(terremotos, aes(anio, num)) + geom_line()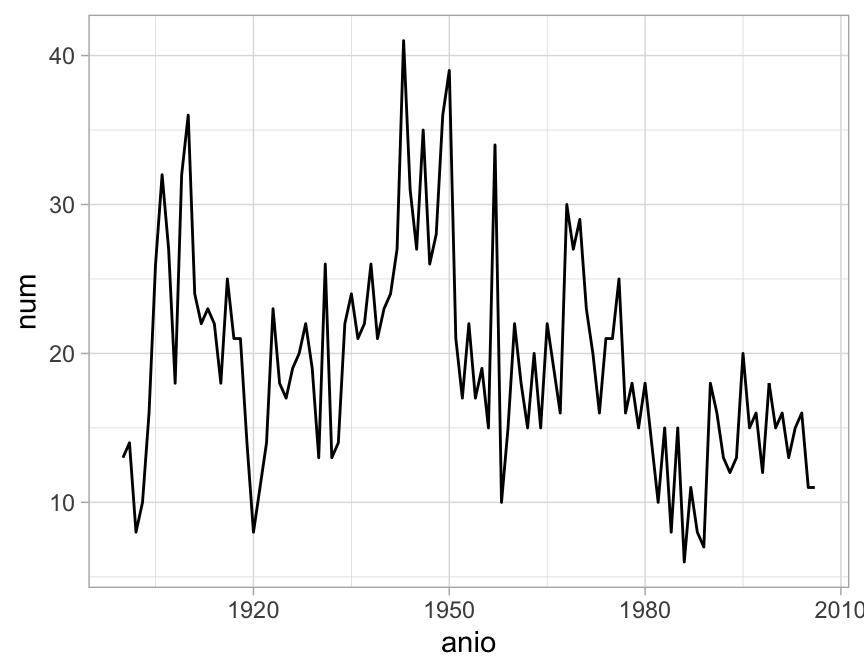

Es natural intentar modelar estos conteos con una distribución Poisson. Sin embargo, un modelo Poisson para observaciones independientes no ajusta a los datos:

library(ggplot2)
library(plyr)
#> -------------------------------------------------------------------------
#> You have loaded plyr after dplyr - this is likely to cause problems.
#> If you need functions from both plyr and dplyr, please load plyr first, then dplyr:
#> library(plyr); library(dplyr)
#> -------------------------------------------------------------------------
#> 
#> Attaching package: 'plyr'
#> The following objects are masked from 'package:dplyr':
#> 
#>     arrange, count, desc, failwith, id, mutate, rename, summarise,
#>     summarize
#> The following object is masked from 'package:purrr':
#> 
#>     compact
library(dplyr)
library(nullabor)

set.seed(12875498)
lambda_1 <- mean(terremotos$num)
# pruebas de hipótesis visuales
terremotos_null <- lineup(null_dist('num', dist = 'poisson', 
  params = list(lambda = lambda_1)), 
  n = 20, terremotos)
#> decrypt("fEo5 4696 Yx UnLY9Ynx Q2")

ggplot(terremotos_null, aes(x = num)) +
  geom_histogram(binwidth = 3) +
  facet_wrap(~.sample)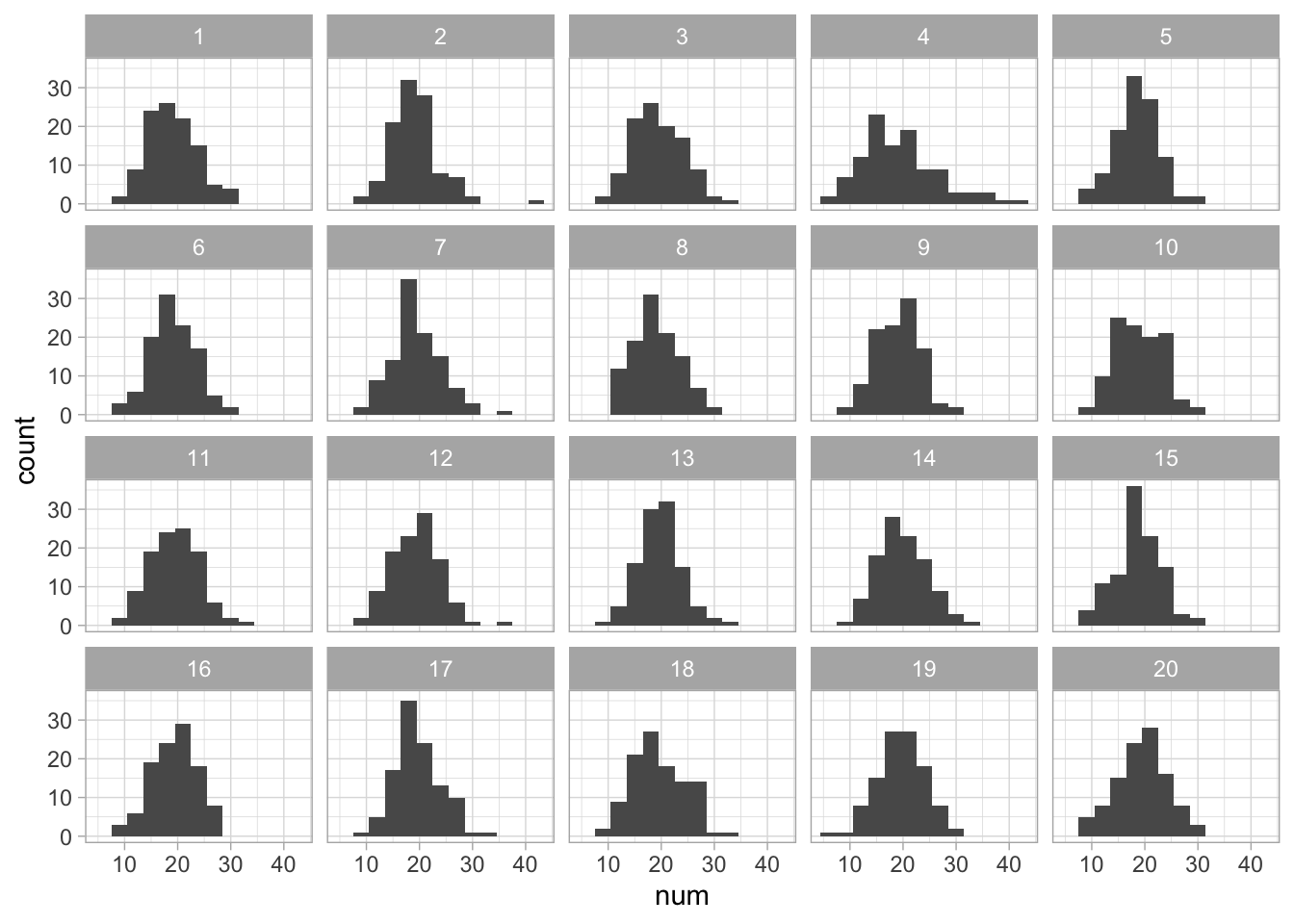

Vemos que los datos presentan sobredispersión en relación a la distribución del modelo. Para lidiar con esta sobredispersión, podemos usar un modelo de clases latentes.

Consideramos un modelo \(C\to X\), donde \(C\) es la clase latente y \(X\) es la observación. La observación la suponemos Poison con una media dependiendo de la clase. Ajustamos por EM y seleccionamos un modelo:

library(flexmix)
#> Loading required package: lattice
model_1 <- FLXMRglm(family = "poisson")
# usa algoritmo EM para ajustar (5 repeticiones con distintos arranques):
# número de clases latentes: de 1 a 6.
modelos_fit <- initFlexmix(num ~ 1, data = terremotos, k = 1:6, model = model_1, 
  nrep = 5)
#> 1 : * * * * *
#> 2 : * * * * *
#> 3 : * * * * *
#> 4 : * * * * *
#> 5 : * * * * *
#> 6 : * * * * *
#> * * * * * *
modelos_fit
#> 
#> Call:
#> initFlexmix(num ~ 1, data = terremotos, model = model_1, 
#>     k = 1:6, nrep = 5)
#> 
#>   iter converged k k0    logLik      AIC      BIC      ICL
#> 1    2      TRUE 1  1 -391.9189 785.8379 788.5107 788.5107
#> 2   34      TRUE 2  2 -360.3708 726.7416 734.7601 767.1610
#> 3   39      TRUE 3  3 -356.8499 723.6998 737.0640 791.9771
#> 4   40      TRUE 4  4 -356.8422 727.6844 746.3942 879.7593
#> 5   28      TRUE 5  5 -356.8365 731.6730 755.7285 932.2082
#> 6   83      TRUE 6  6 -356.8310 735.6621 765.0632 962.2977

Así que podríamos escoger, por ejemplo, el modelo de tres clases:

mod_1 <- getModel(modelos_fit, which='3')
mod_1
#> 
#> Call:
#> initFlexmix(num ~ 1, data = terremotos, model = model_1, 
#>     k = 3, nrep = 5)
#> 
#> Cluster sizes:
#>  1  2  3 
#> 26 11 70 
#> 
#> convergence after 39 iterations
probs_clase <- mod_1@prior
medias_pois <- mod_1@components
probs_clase
#> [1] 0.2774396 0.1318420 0.5907184
medias_pois
#> $Comp.1
#> $Comp.1[[1]]
#> $coef
#> (Intercept) 
#>    2.545102 
#> 
#> 
#> 
#> $Comp.2
#> $Comp.2[[1]]
#> $coef
#> (Intercept) 
#>    3.450563 
#> 
#> 
#> 
#> $Comp.3
#> $Comp.3[[1]]
#> $coef
#> (Intercept) 
#>    2.983465

Para entender cómo quedó el ajuste, podemos graficar la serie original junto con la media poisson condicional de cada clase, por ejemplo:

terremotos$clase_1 <- clusters(mod_1)

terremotos$medias_est <- sapply(terremotos$clase_1, function(cl){
  exp(mod_1@components[[cl]][[1]]@parameters$coef[1])
})

ggplot(terremotos, aes(anio, num)) + 
  geom_line(alpha = 0.8) +
  geom_line(aes(anio, medias_est), color = "red", alpha= 0.8)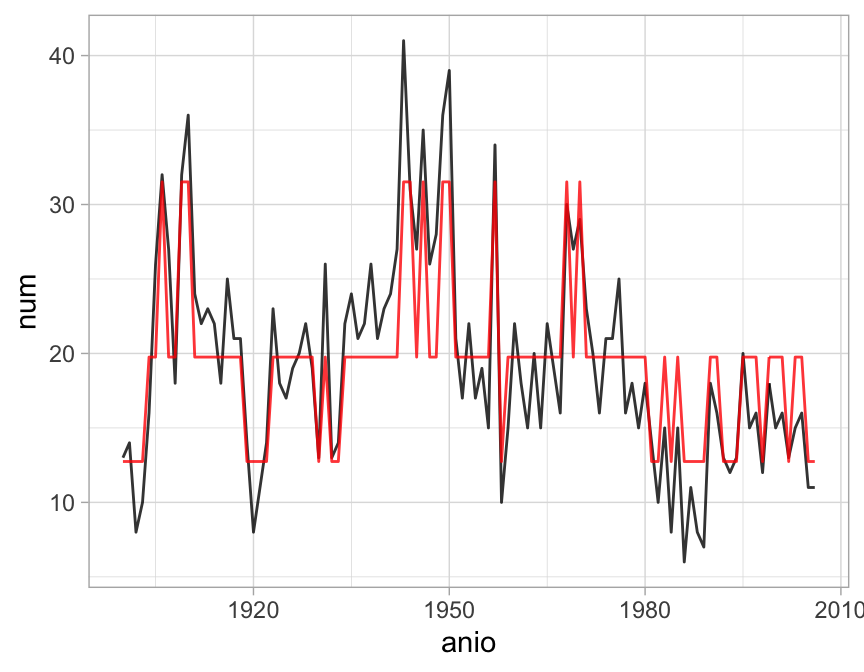

Simulamos de estos datos y vemos que ya no hay sobredispersión (es decir, este modelo ajusta mejor que el de una sola clase):

terremotos_null <- lineup(null_dist('num', dist = 'poisson', 
  params = list(lambda = terremotos$medias_est)), 
  n = 20, terremotos)
#> decrypt("fEo5 4696 Yx UnLY9Ynx zZ")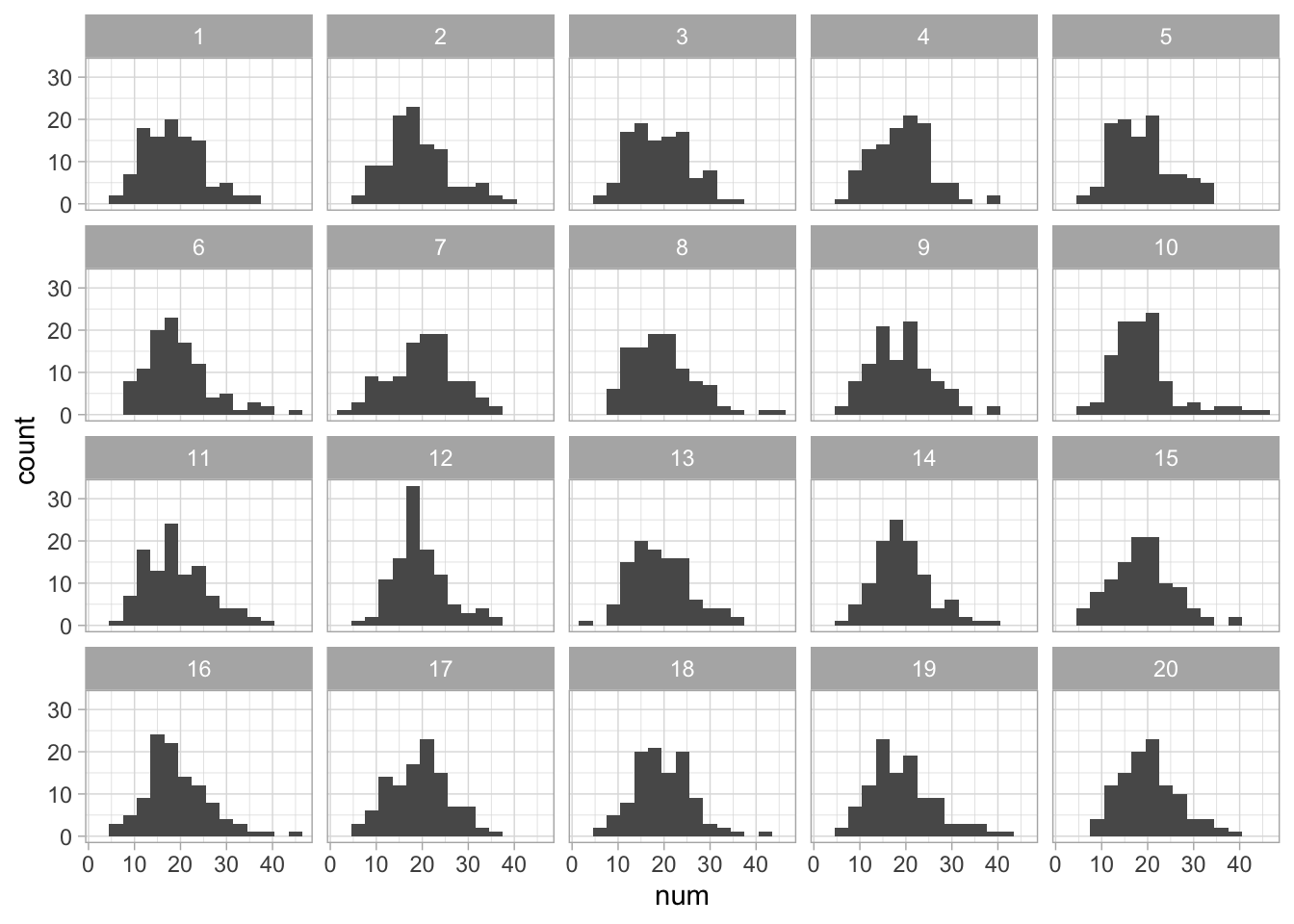

ggplot(terremotos_null, aes(x = num)) +
  geom_histogram(binwidth = 3) +
  facet_wrap(~.sample)

Si una variable \(Y\) es Poisson, su media es igual a su varianza. Ahora supón que \(Y\) es una mezcla discreta Poisson: si la clase latente la denotamos por \(S\) y la observación por \(Y\), entonces \(Y|S=s\) es Poisson con media \(\lambda_s\), para \(s=1\ldots,M\). Muestra que en general la varianza de \(Y\) es más grande que su media (está sobredispersa). Explica en palabras de dónde viene esa sobredispersión.

7.1.1 Dependencia temporal

Existe un aspecto adicional que no hemos considerado: dependencia de observaciones contiguas en las serie. Podríamos gráficar para la serie de terremotos las pares \((X_t, X_{t+1})\):

ggplot(terremotos, aes(lag(num), num)) +
  geom_point() +
  geom_smooth()
#> `geom_smooth()` using method = 'loess' and formula 'y ~ x'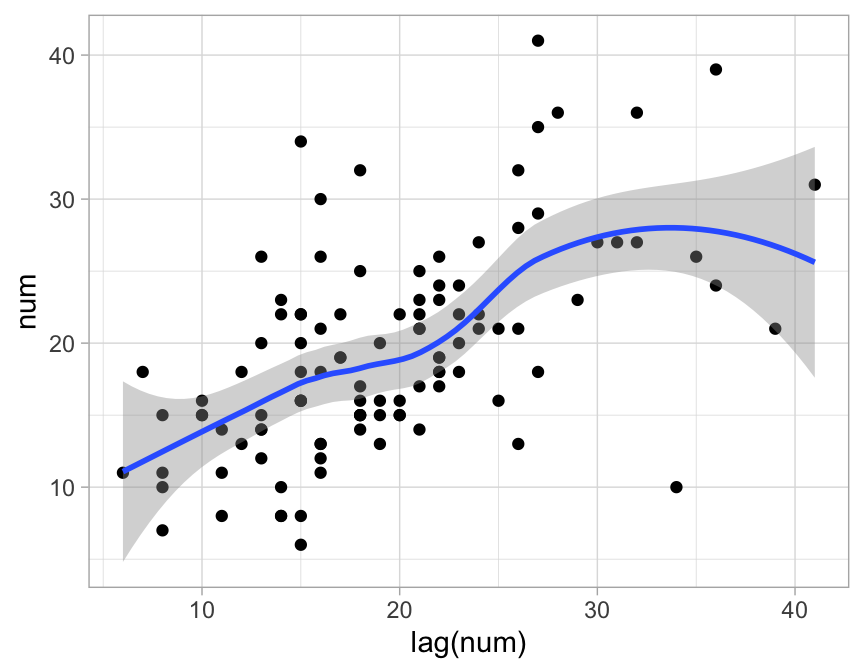

Esta gráfica explica por qué si hacemos simulaciones de nuestro modelo ajustado (tomando en cuenta el orden temporal), estas simulaciones son claramente diferentes que los datos observados:

ggplot(terremotos_null, aes(anio, num)) +
  geom_line(size=0.3) +
  facet_wrap(~.sample)

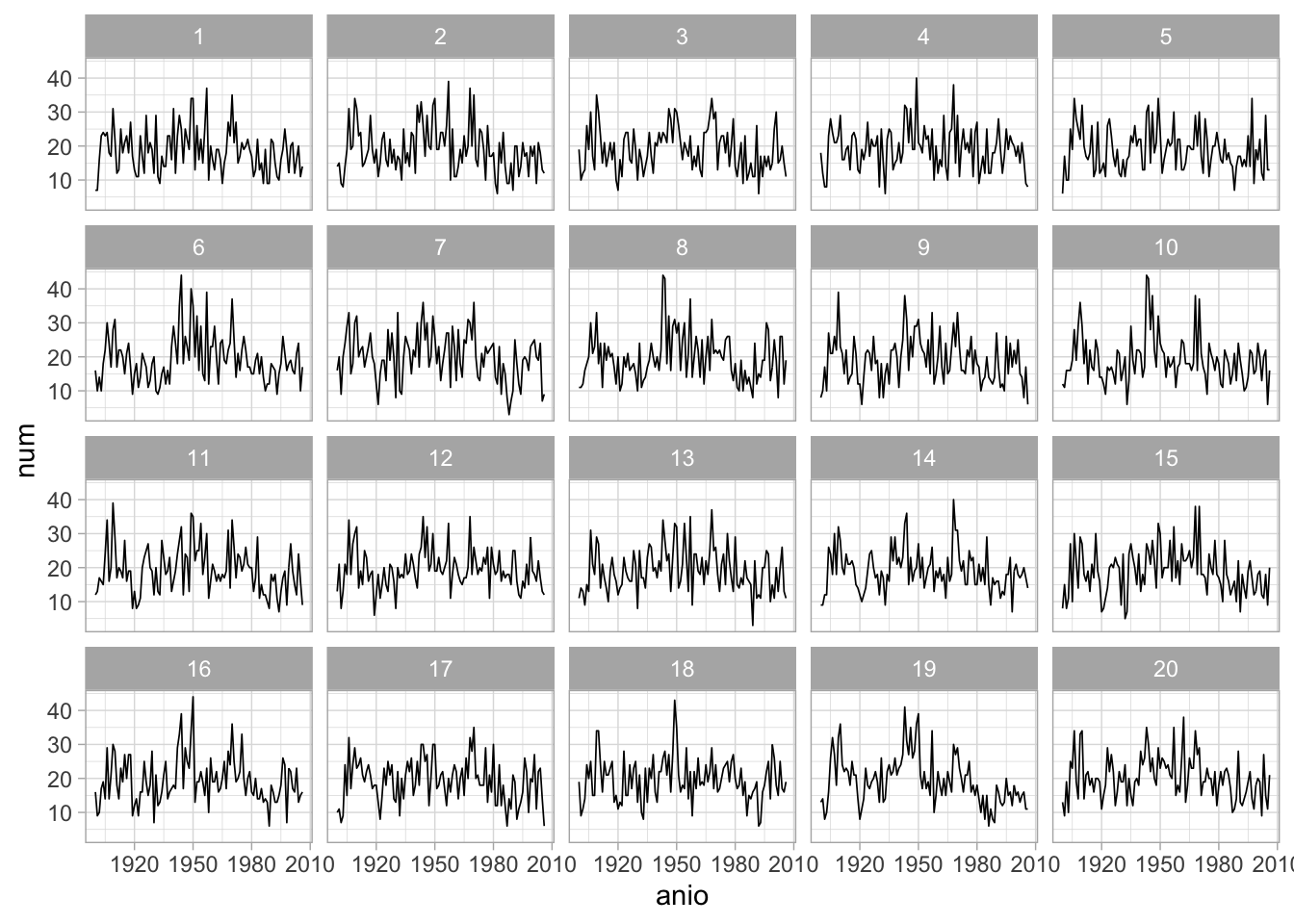
Si nos interesa hacer predicciones, el modelo de mezcla no es un buen camino, pues no utiliza adecuadamente la información más reciente para hacer los pronósticos.

Otra manera de verificar que las observaciones tienen mayor grado de correlación temporal que los simulados del modelo de mezcla es a través de los siguientes cálculos.

terremotos_null %>%
  group_by(.sample) %>%
  mutate(num_lag = lag(num)) %>%
  filter(!is.na(num_lag)) %>%
  summarise(cor = cor(num, num_lag)) %>%
  arrange(desc(cor))
#>         cor
#> 1 0.2510768

Y notamos que justamente los datos con mayor correlación corresponden a los datos observados (.sample = decrypt("n20q ilOl TJ IH4TOTHJ 1")).

Ahora evaluamos la tasa de error de predicción a un paso de este modelo usando validación cruzada para datos temporales. En este caso, la predicción es simplemente la media Poisson de la clase más popular:

preds_1  <- sapply(50:106 ,function(i){
  mod_1 <- flexmix(num~1, data = terremotos[1:i, , drop = FALSE], k = 3,                 
    model = model_1)
  mod_1
  clase_1 <- which.max(table(mod_1@cluster))
  mod_1@components[[clase_1]][[1]]@parameters[[1]]
})

Error medio absoluto:

mean(abs(exp(preds_1) - terremotos[51:107, "num"]))
#> [1] 5.669461

Autocorrelación muestral

Una manera popular de diagnosticar observaciones temporalmente correlacionadas es usando la función de autocorrelación muestral. Usualmente la correlación la calculamos para pares de observaciones \((X_i,Y_i)\). En el caso de la autocorrelación, calculamos la correlación entre una serie y versiones rezagadas de la misma variable, es decir, consideramos los pares \((X_i,X_{i-k})\) para distintos valores de \(k=1,2,\ldots\). La autcorrelación muestral se define:

\[r_k=\frac{\sum_{t=k+1}^{T}(x_t-\overline{x})(x_{t-k}-\overline{x})}{\sum_{t=1}^T(x_t-\overline{x})},\]

podemos graficar la serie \(r_k\) para descubrir estructura en la serie que estamos analizando. En nuestro ejemplo:

acf(terremotos$num)

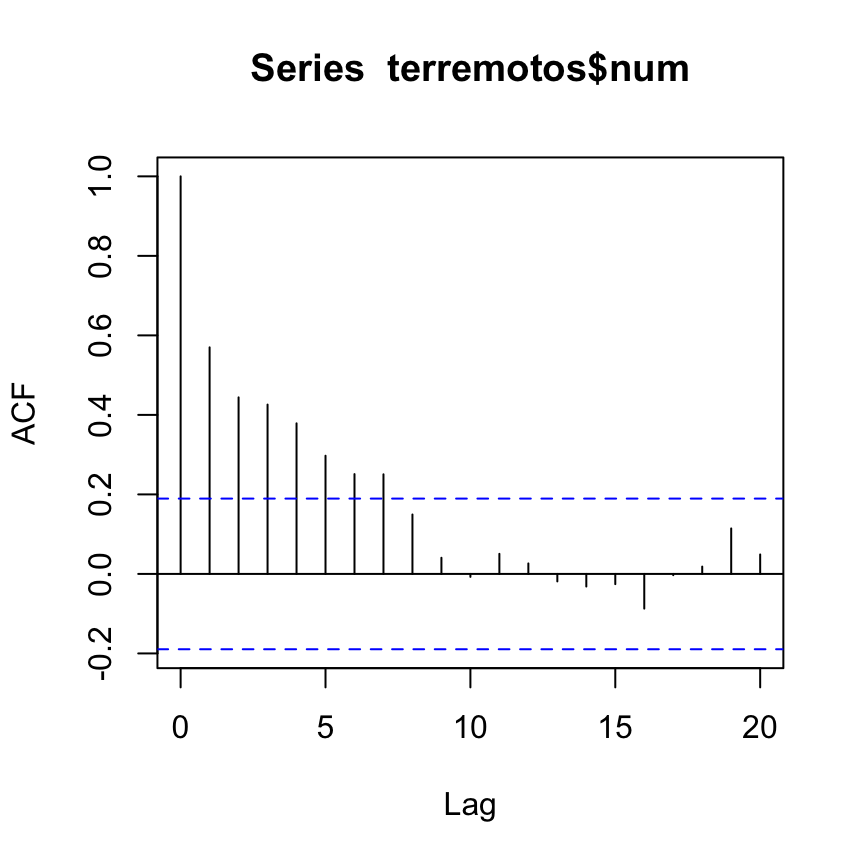
El primer valor (\(k=1\)) siempre es igual a 1. Observamos sin embargo autocorrelacciones considerables de orden 1 a 5.

¿Cómo se ve esta gráfica cuando tenemos observaciones independientes? Esperamos observar coeficientes de correlación relativamente chicos:

set.seed(280572)
par(mfrow=c(1,2))
acf(rnorm(150))
acf(rpois(150, 20))

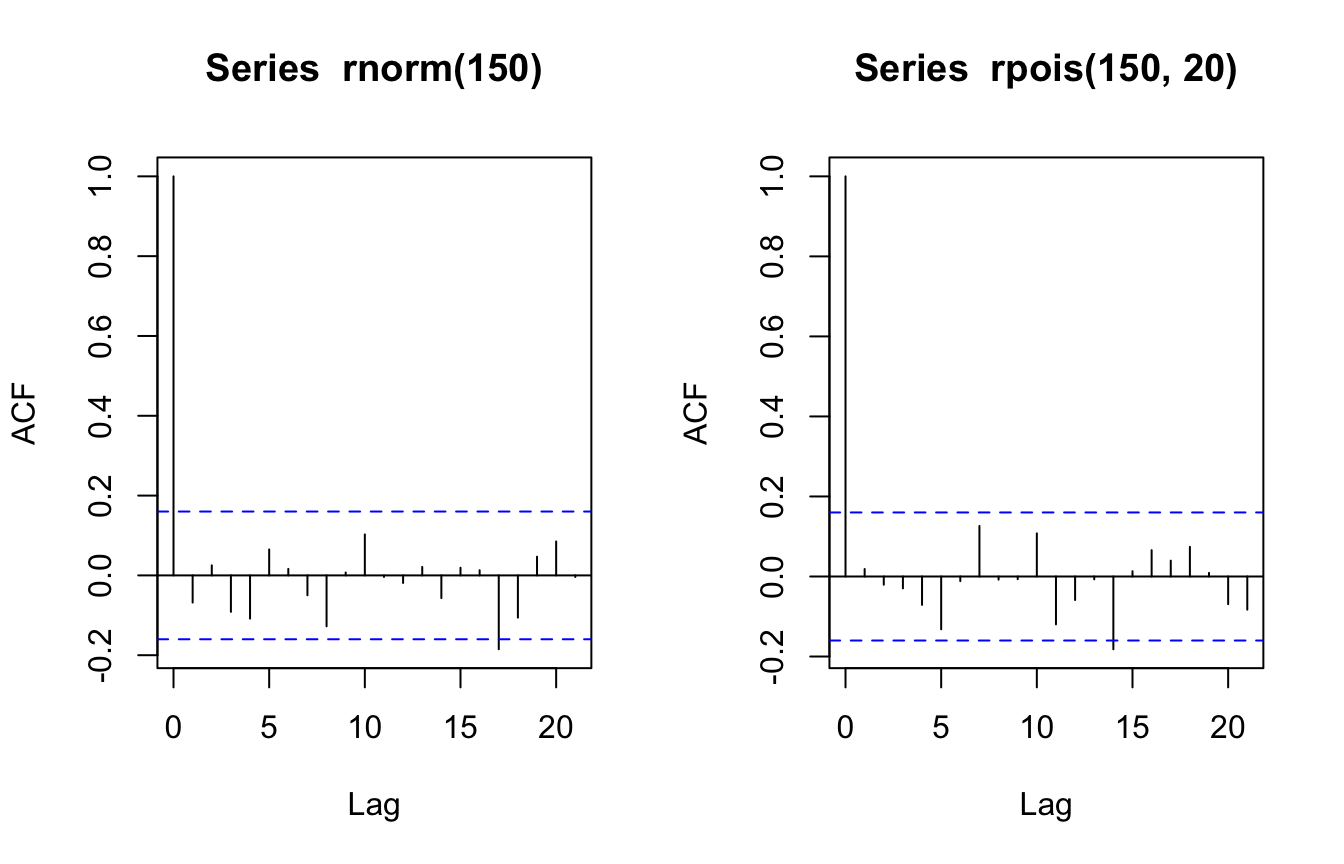
Modelando la dependencia temporal

Si queremos capturar la estrucutra temporal de los datos, o hacer predicciones para datos futuros, es necesario modelar la estructura temporal explícita o implícitamente. Por ejemplo,podríamos intentar construir el modelo:

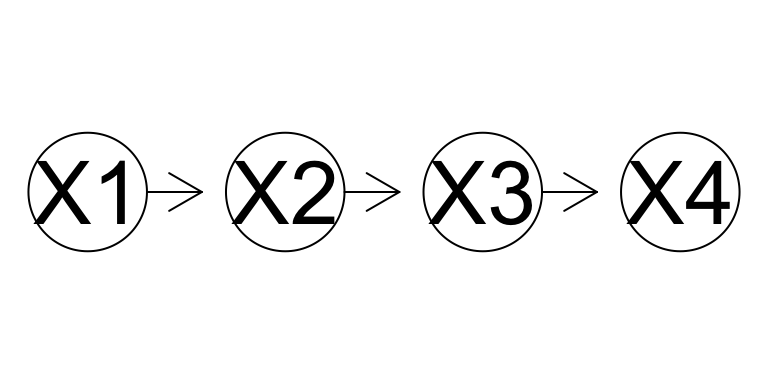
O de manera más general, tomando en cuanto dependencias más largas:

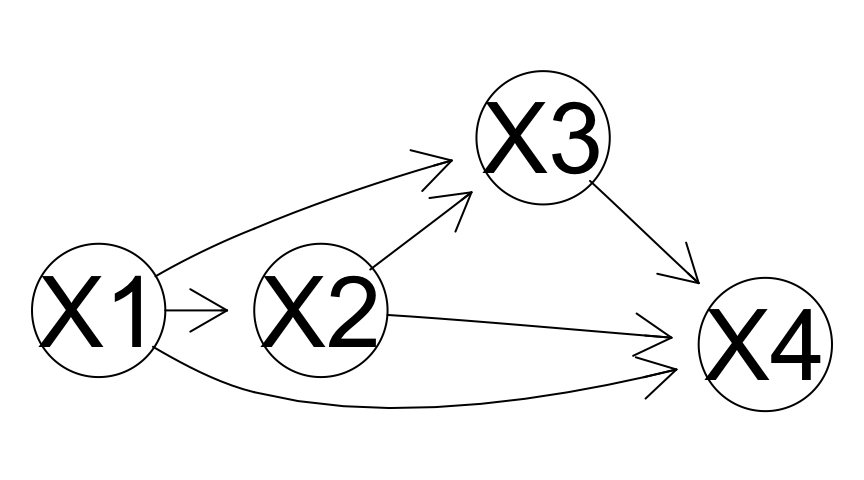
Sin embargo, utilizaremos un enfoque de variables latentes. La idea es introducir un estado latente, a partir del cual generamos las observaciones. Por ejemplo:

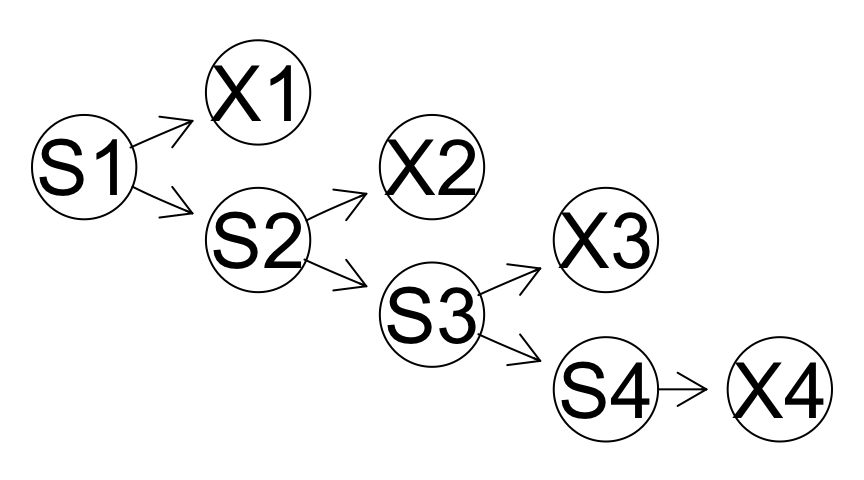
En un modelo como este, pueden existir dependencias más largas entre las \(X_t\), aún cuando la estructura es relativamente simple.

¿cuáles son las independencias condicionales mostradas en la gráfica? ¿Las \(X_i\) son independientes entre ellas?}