8.2 Estimación de \(\mu(s)\)
Suponemos que \(\mu(s)\) es una función suave, continua que varía espacialmente. Podemos modelar \(\mu(s)\) usando polinomios locales, splines o cualquier función de covariables y parámetros.
Las covariables pueden incluir las coordenadas geográficas y variables que expliquen la variabilidad espacial (por ejemplo, si analizamos contaminación del aire podemos usar temperatura o dirección del aire.)
Adicionalmente se pueden añadir otras covariables que contribuyan a explicar la variación en el proceso (por ejemplo, si estamos analizando concentración de contaminantes en el aire podemos incluir covariables como temperatura o dirección del viento).
Veamos un ejemplo donde se midió el pH del agua en 250 sitios.
soil <- read.table("data/Soil_data.txt", header=T)
head(soil)
#> x y elevation sand silt clay pH_water pH_KCl calcium magnesium
#> 1 0 0 578.295 9 26 43 5.8 4.9 3.6 0.8
#> 2 0 5 578.460 9 26 42 5.9 4.9 3.4 0.8
#> 3 0 10 578.491 9 25 41 5.9 4.9 3.7 0.9
#> 4 0 15 578.699 11 28 40 5.8 4.9 3.7 0.8
#> 5 0 20 578.749 9 27 41 5.8 5.0 4.2 0.9
#> 6 0 25 578.726 8 27 43 6.1 5.1 4.1 0.9
#> potassium aluminum hydrogen carbon nitrogen cation_exchange sulfur
#> 1 0.50 0 3.1 1.2 0.12 8.00 4.90
#> 2 0.44 0 3.2 1.1 0.12 7.84 4.64
#> 3 0.59 0 2.5 1.2 0.13 7.69 5.19
#> 4 0.52 0 3.5 1.3 0.12 8.52 5.02
#> 5 0.56 0 3.4 1.4 0.13 9.06 5.66
#> 6 0.56 0 3.1 1.2 0.13 8.66 5.56
#> volume mass NC CEC CN
#> 1 61.250 0 1.050 4.90 10
#> 2 59.184 0 1.272 4.64 9
#> 3 67.490 0 0.289 5.19 9
#> 4 58.920 0 1.416 5.02 10
#> 5 62.472 0 1.023 5.66 10
#> 6 64.203 0 0.753 5.56 9
# Vamos a modelar el PH del agua
class.ph <- classIntervals(soil$pH_water, 9, style = "fixed",
fixedBreaks = seq(min(soil$pH_water), max(soil$pH_water), length = 10))
soil$ph <- cut(soil$pH_water, class.ph$brks, include.lowest = TRUE)Comenzamos con un análisis exploratorio:
- Gráficas de los datos y de curvas de nivel nos pueden ayudar en la detección de atípicos espaciales.
ggplot(soil, aes(x = x, y = y, color = ph)) +
geom_point(size = 2.3) +
scale_colour_brewer(palette="Blues")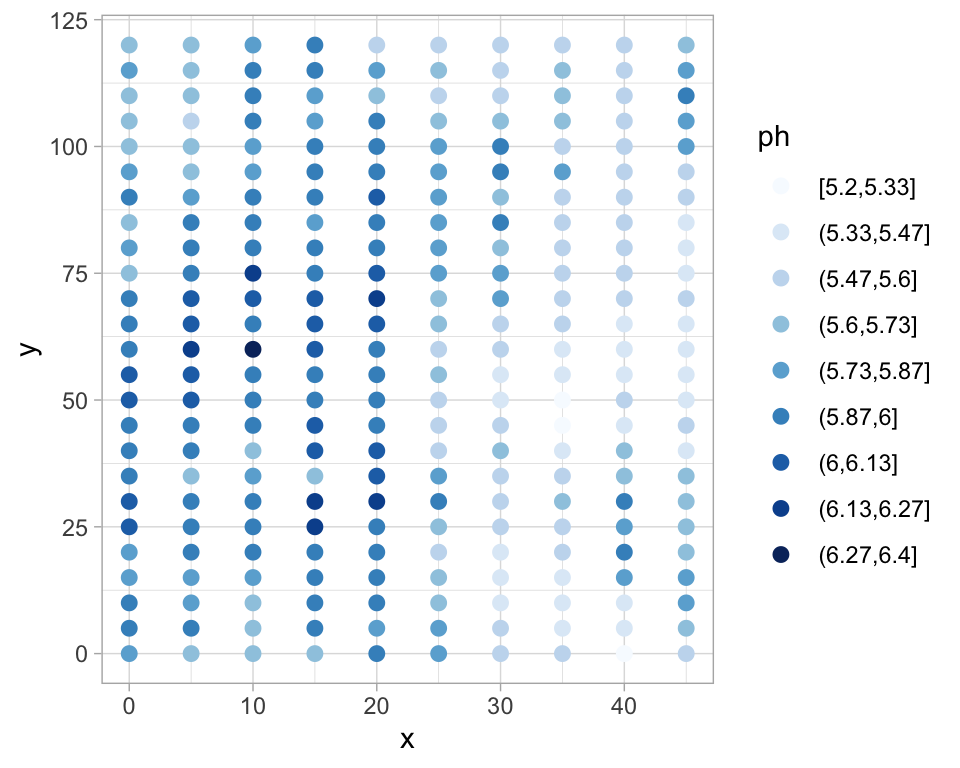 
library(akima)
# Interpolar los valores observados (akima)
surf.ph <- interp(soil$x, soil$y, soil$pH_water)
# hacer una gráfica
surf.ph.r <- cbind(expand.grid(surf.ph$x, surf.ph$y), c(surf.ph$z))
colnames(surf.ph.r) <- c("x", "y", "z")
surf.ph.r$ph <- cut(surf.ph.r$z, class.ph$brks)
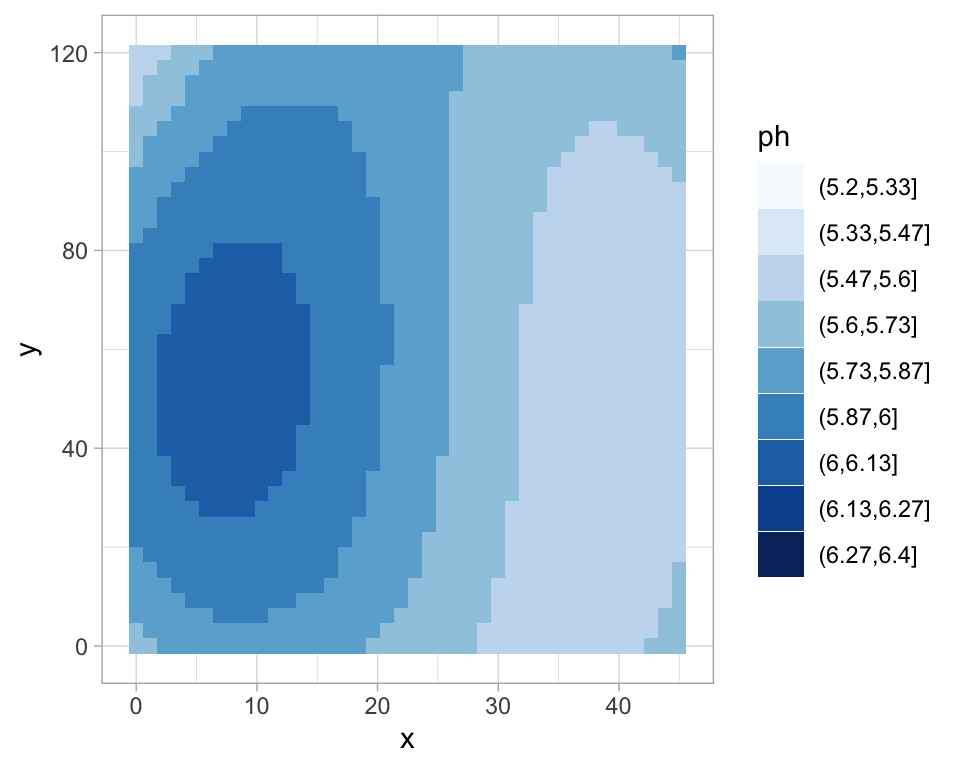
ggplot(surf.ph.r, aes(x = x, y = y, z = z)) +
geom_tile(aes(fill = ph)) + scale_fill_brewer(palette = "Blues") +
stat_contour()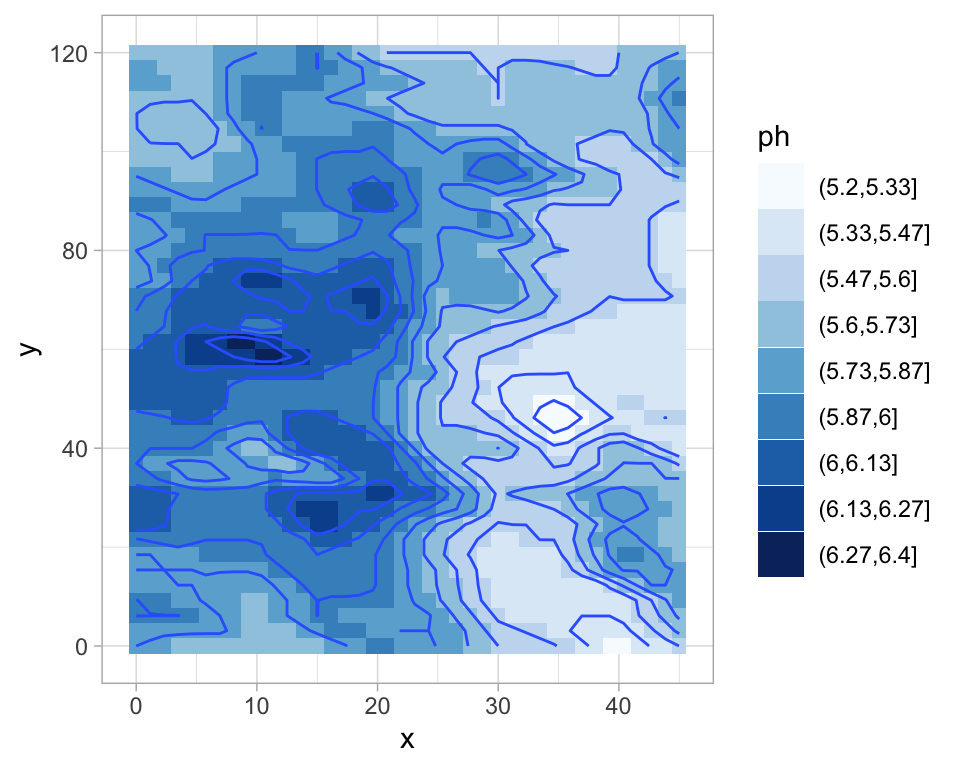 
- Podemos explorar la dependencia espacial de \(\mu(s)\) en las coordenadas geográficas graficando \(Y(s_i)\) contra las coordenadas, o si los datos están muestreados sobre una cuadrícula graficando la media y mediana de la fila contra el ínidce de la fila o columna.
# EDA: gráficas de la media/mediana del pH vs el número de fila y de columna
x.est <- soil %>%
group_by(x) %>%
dplyr::summarise(
media = mean(pH_water),
mediana = median(pH_water)
) %>%
gather(variable, valor, -x)
y.est <- soil %>%
group_by(y) %>%
dplyr::summarise(
media = mean(pH_water),
mediana = median(pH_water)
) %>%
gather(variable, valor, -y)
x <- ggplot(x.est, aes(x = x, y = valor, color = variable)) +
geom_point() + geom_line()
y <- ggplot(y.est, aes(x = y, y = valor, color = variable)) +
geom_point() + geom_line()
grid.arrange(x, y, ncol = 2)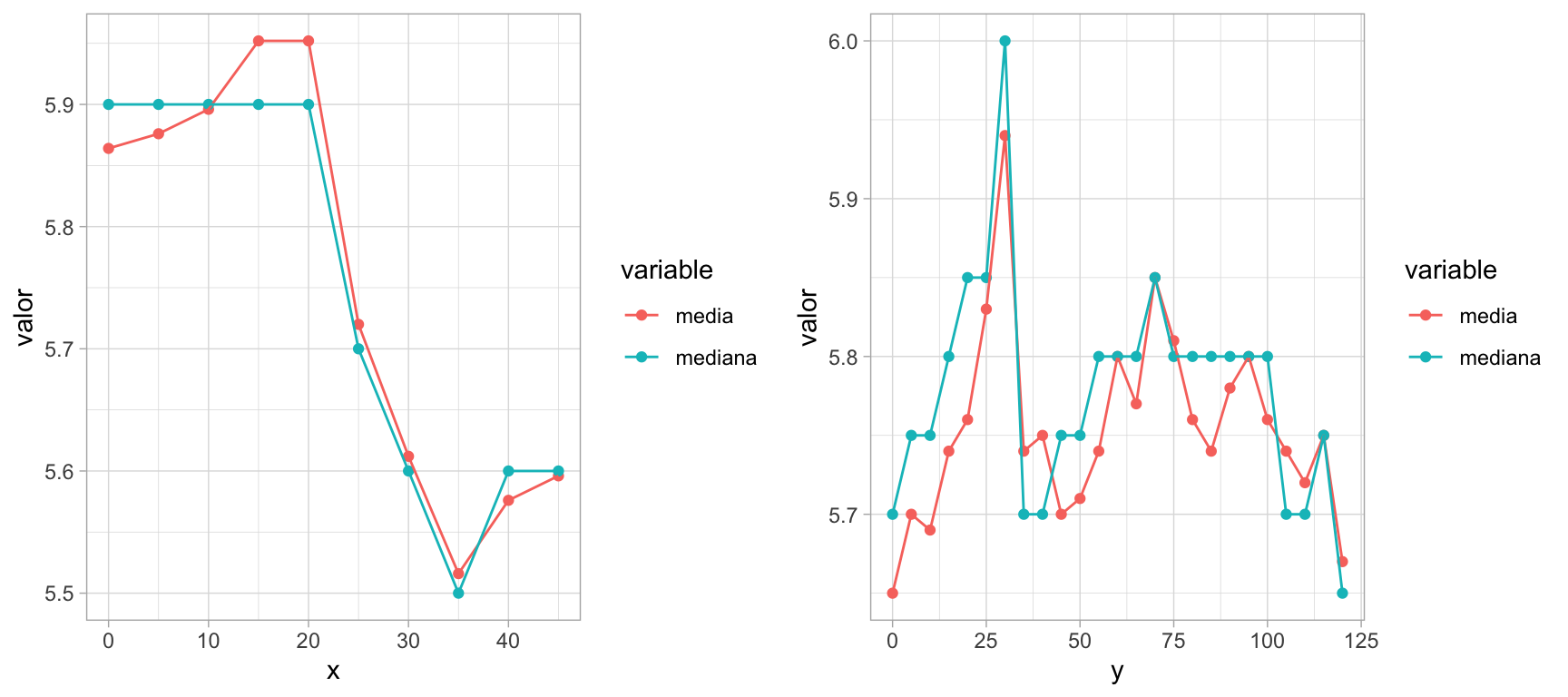
Podemos modelar \(\mu(s)\) como una función lineal de las covariables. Por ejemplo, si modelamos \(\mu(s)\) como una función lineal únicamente de las coordenadas tenemos:
\[\mu(s) = \beta_0 + \beta_1 s_x + \beta_2 s_y + \beta_3 s_x^2 + \beta_4 s_y^2 + \beta_5 s_x s_y\]
Cuando se utiliza un polinomio de las coordenadas geográficas es conveniente utilizar un polinomio completo, esto es, incluir todos los monomios de grado menor o igual al grado del polinomio. Esto garantiza que la superficie que ajustamos es invariante a la elección del origen y la orientación de las coordenadas (transformaciones lineales).
Es común centrar las coordenadas geográficas restando la media.
Supongamos que queremos modelar la tendencia espacial utilizando únicamente información de las coordenadas, sea \(X(s)\) un vector de tamaño \(p \times 1\) que contiene la información geográfica. Entonces, para obtener una estimación provisional de la tendencia espacial de \(Y(s)\) podemos ajustar un modelo de regresión: \[Y(s) = \mu(s) + \epsilon(s) = X(s)^T\beta + \epsilon(s)\] donde \(\epsilon(s)\) son iid. Notemos que si queremos incorporar otras covariables (además de información de las coordenadas), simplemente las añadimos a la matriz \(X(s)\).
Volvamos al ejemplo del ph del agua.
#### Estimación de la tendencia espacial
mod.1 <- lm(pH_water ~ x + y, data = soil)
# La tendencia espacial estimada está dada por los valores ajustados y podemos
# obtener una superficie utilizando interpolación bilineal o predict
surf.ph.r$z <- predict(mod.1, surf.ph.r[, 1:2])
# Discretizamos pH utilzando los mismos cortes que el plot exploratorio
surf.ph.r$z <- predict(mod.1, surf.ph.r[, 1:2])
surf.ph.r$ph <- cut(surf.ph.r$z, class.ph$brks)
ggplot(surf.ph.r, aes(x = x, y = y, z = z)) +
geom_tile(aes(fill = ph)) +
scale_fill_brewer(palette = "Blues", drop = FALSE)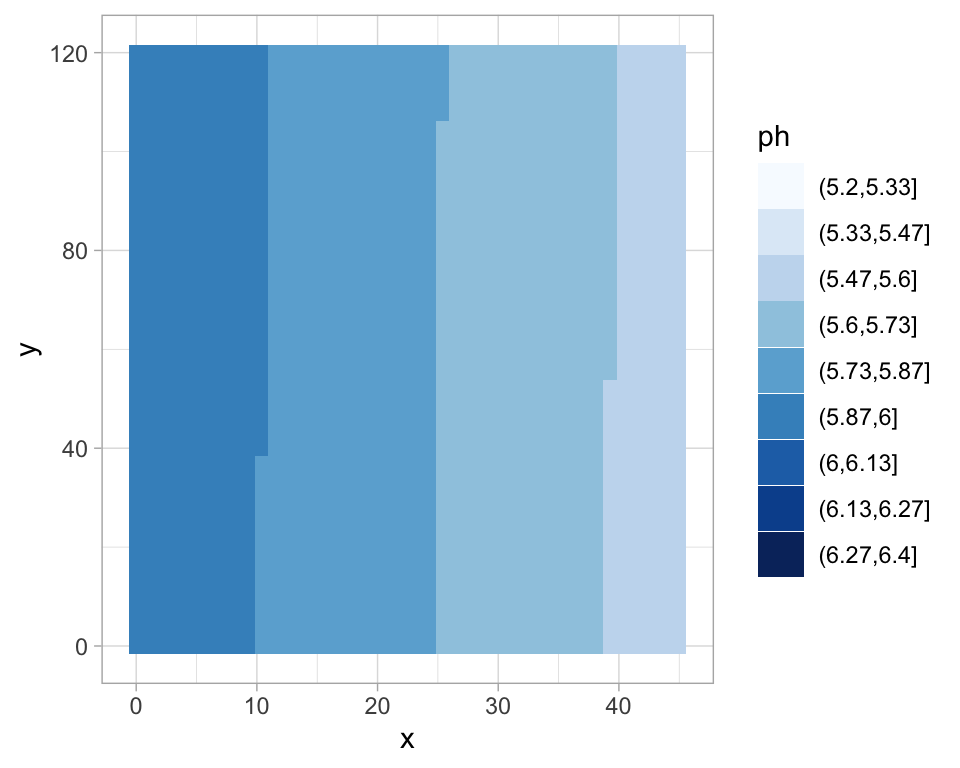
# Polinomio de segundo orden
mod.1 <- lm(pH_water ~ 1 + x + y + I(x * y) + I(x ^ 2) + I(y ^ 2), data = soil)
surf.ph.r$z <- predict(mod.1, surf.ph.r)
surf.ph.r$ph <- cut(surf.ph.r$z, class.ph$brks)
ggplot(surf.ph.r, aes(x = x, y = y, z = z)) +
geom_tile(aes(fill = ph)) +
scale_fill_brewer(palette = "Blues", drop = FALSE)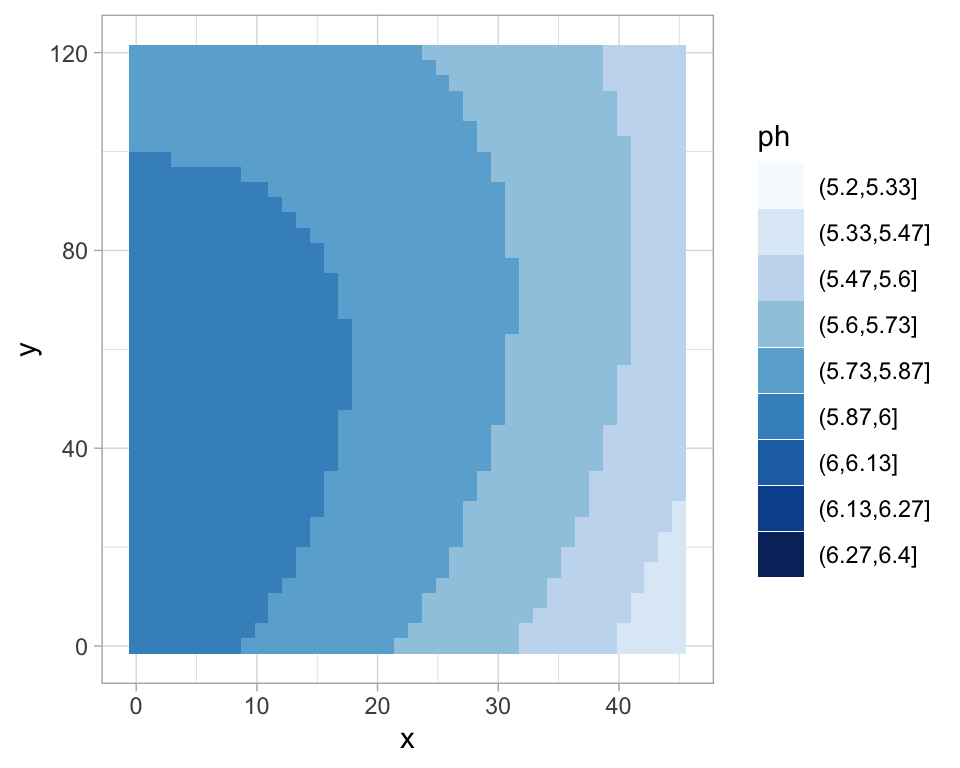
# Polinomio de tercer orden
mod.1 <- lm(pH_water ~ 1 + x + y + I(x * y) + I(x ^ 2) + I(y ^ 2) + I(x ^2 * y) +
I(x * y ^ 2) + I(x ^ 3) + I(y ^ 3), data = soil)
surf.ph.r$z <- predict(mod.1, surf.ph.r)
surf.ph.r$ph <- cut(surf.ph.r$z, class.ph$brks)
ggplot(surf.ph.r, aes(x = x, y = y, z = z)) +
geom_tile(aes(fill = ph)) +
scale_fill_brewer(palette = "Blues", drop = FALSE)