2.1 Gráficas dirigidas
Una gráfica dirigida es un conjunto de vértices junto con un subconjunto de aristas dirigidas (pares ordenados de vértices). En nuestro caso, cada vértice corresponde a una variable aleatoria, y cada arista dirigida representa una asociación probabilística entre las variables (vértices) que conecta. Nos interesan en particular las gráficas dirigidas acíclicas (GADs), estas son aquellas que no tienen caminos dirigidos partiendo de un vértice y regresando al mismo (ciclos).
Ejemplo.
library(igraph, warn.conflicts = FALSE)
library(bnlearn)
#>
#> Attaching package: 'bnlearn'
#> The following objects are masked from 'package:igraph':
#>
#> compare, degree, path, subgraph
#> The following object is masked from 'package:stats':
#>
#> sigma
gr <- graph(c(1, 2, 3, 2, 3, 4))
plot(gr,
vertex.label = c('Dieta', 'Enf. corazón', 'Fuma', 'Tos'),
layout = matrix(c(0, 0.5, 2, 0, 4, 0.5, 6, 0), byrow = TRUE, ncol = 2),
vertex.size = 23, vertex.color = 'salmon', vertex.label.cex = 1.2,
vertex.label.color = 'gray40', vertex.frame.color = NA, asp = 0.5,
edge.arrow.size = 1)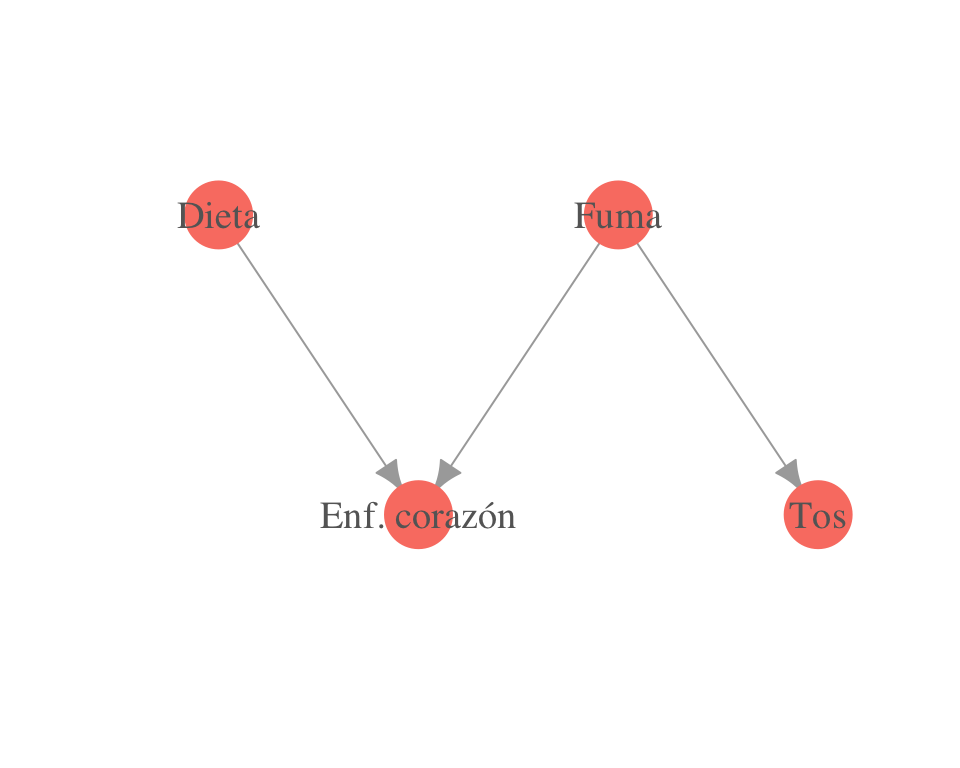
Nos interesan estas gráficas por lo que pueden representar acerca de la estructura de la distribución conjunta de las variables. Recordemos que la distribución conjunta es el modelo completo del fenómeno, a partir de la cual podemos contestar cualquier pregunta de inferencia, asociación, independencia, etc.
En las siguientes secciones explicaremos dos enfoques para interpretar una gráfica dirigida probabilísticamente (en términos de la distribución conjunta).
Por una parte la gráfica define un esqueleto que sirve para representar de manera compacta una distribución de dimensión alta, esto es: En lugar de codificar la probabilidad de todos los posibles valores de las variables en nuestro dominio, podemos separar la distribución en factores más chicos, cada uno sobre un conjunto de posibilidades mucho más chico. Una vez que definimos los factores podemos definir la distribución conjunta como el producto de los factores.
La segunda perspectiva es que la gráfica es una representación compacta de un conjunto de independencias que se sostienen en la distribución (la distribución que codifica nuestras creencias de una situación particular).
2.1.1 Probabilidad conjunta y factorizaciones
Siempre es posible representar a una distribución conjunta como un producto de condicionales de una sola variable. Dado un ordenamiento , podemos escribir (por la regla del producto)
Por ejemplo, si tenemos tres variables podemos usar la regla del
producto para obtener
también podemos ordenar las variables de manera distinta y escribir:
Estas son representaciones válidas para la conjunta de . Para modelar podríamos entonces estimar primero la marginal de , después entender la condicional de dada y finalmente la condicional de dado y . Algunas representaciones son más fáciles para trabajar, calcular y entender que otras.
Ejemplo. Si sacamos sucesivamente tres cartas de una baraja y registramos si son rojas o negras, lo más fácil es definir = color de la -ésima carta, y entonces si buscamos calcular simplemente calculamos: y finalmente de modo que la probabilidad que nos interesa es
Otro caso en que la factorización que escogemos es importante, es cuando existen independencias condicionales, la factorización puede resultar en un modelo más compacto o más conveniente.
Ejemplo. Si y son independentes y es condicionalmente independiente de dado , podemos comenzar con la segunda factorización
y finalmente
el cual es un modelo considerablemente más simple que el original pues incluye dos marginales y sólo es necesario modelar cómo depende de . Esto lo expresamos en el siguiente resultado:
Una factorización de la conjunta puede ser entendida como una parametrización particular de la conjunta a través de sus distribuciones condicionales.
Ejemplo. Supongamos la factorización , y que y son variables binarias que toman los valores y . La parametrización usual para está dada por donde y (3 parámetros en total). De esta forma tenemos que especificar, por ejemplo, los parámetros .
Por otra parte, la factorización sugiere los parámetros donde , y . Los otros parámetros están dados por , y .
Nótese que la idea general es
Usar la regla de la cadena, lo que siempre nos da una expresión válida para la conjunta, y en la cual aparece la condicional de cada variable una sola vez para una ordenamiento adecuado de las variables.
Simplificar la expresión obtenida usando las independencias condicionales que suponemos.
- Hacer los cálculos/inferencia, etc. usando la parametrización de condicionales.
2.1.2 Factorizaciones de la conjunta y gráficas dirigidas.
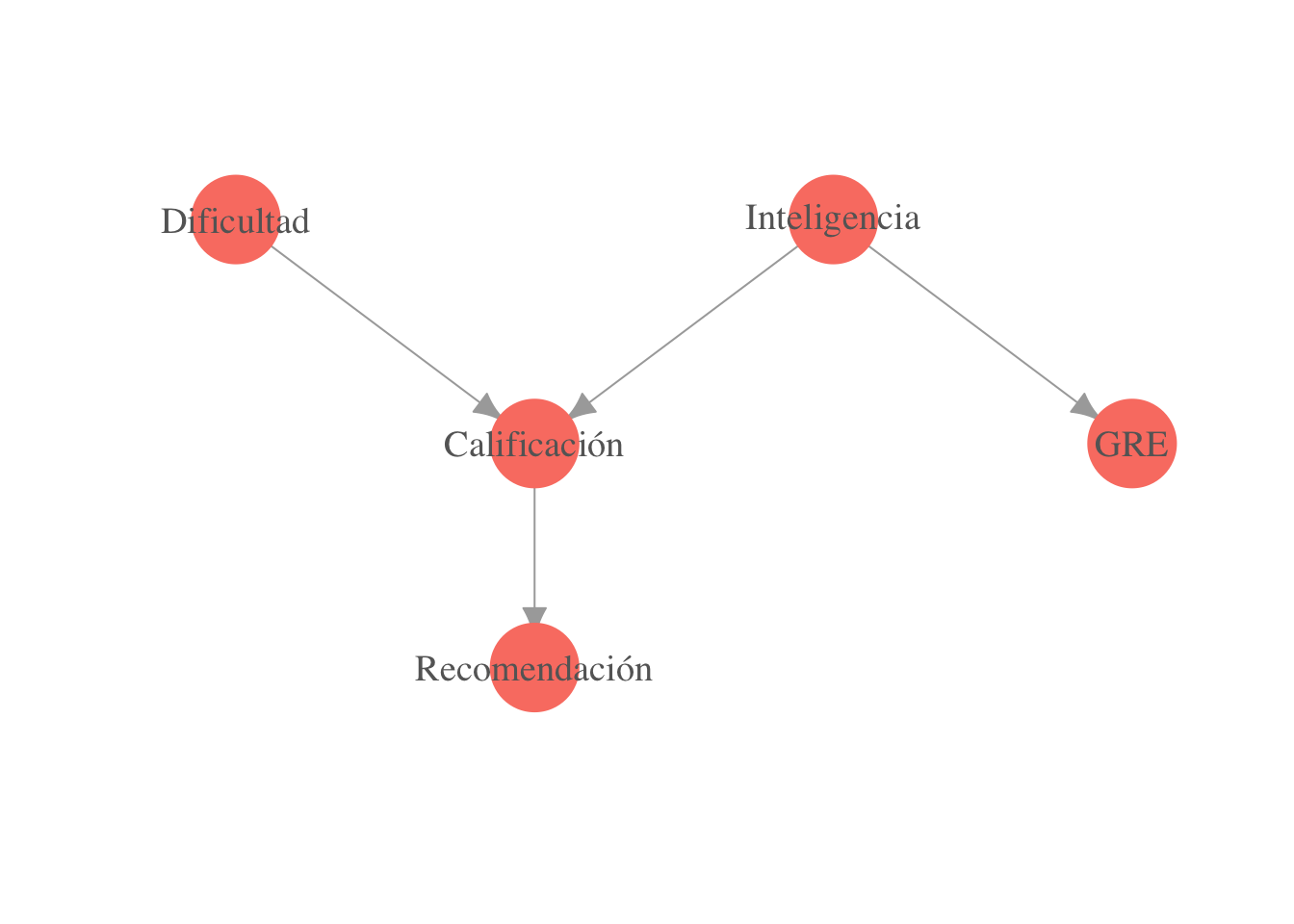
- ¿Qué factorización crees que es apropiada para la distribución conjunta ?
- Ninguna de las anteriores.
En primer lugar, las gráficas dirigidas acíclicas asociadas a una distribución conjunta dan una factorización particular para la conjunta.
Sea una gráfica dirigida con vértices , denotamos por a todos los padres de en .
Sea una distribución conjunta para . Decimos que representa a cuando la conjunta se factoriza como
El conjunto de distribuciones que son representadas por lo denotamos por (llamadas distribuciones markovianas con respecto a ).
Nótese que una gráfica acíclica no dirigida (GAD) no establece una distribución particular, sino un conjunto de posibles distribuciones: todas las distribuciones que se factorizan bajo .
Nota. La factorización del lado derecho del resultado siempre es una distribución de probabilidad. Por ejemplo, si consideramos la siguiente factorización de :
Veremos que es una distribución de probabilidad como sigue: en primer lugar, este producto es no negativo, pues todas son distribuciones condicionales. Basta demostrar que si sumamos sobre todos los posibles valores de , entonces esta expresión suma 1:
Discusión. Ordenamiento topológico de vértices en un gráfica dirigida acíclica.
En este último ejemplo vimos que el cálculo de la suma total se hace empujando primero dentro de la suma los índices de las variables que no tienen descendientes (o que no aparecen como condicionadoras), y trabajando hacia arriba. En términos de la gráfica, trabajamos de los últimos vértices hasta los primeros.
De hecho, una GAD siempre da un ordenamiento (topológico) de los vértices, módulo variables que están al mismo nivel. Por ejemplo, en la gráfica de la figura anterior, los ordenamientos son o . ¿Qué ordenamiento da la siguiente gráfica?
gr <- graph(c(1, 2, 1, 3, 3, 2, 2, 4))
plot(gr,
layout = matrix(c(0, 0.5, 0.5, 0, 0, -0.5, 1, 0), byrow = TRUE, ncol = 2),
vertex.size = 20, vertex.color = 'salmon', vertex.label.cex = 1.2,
vertex.label.color = 'gray40', vertex.frame.color = NA, asp = 0.5,
edge.arrow.size = 1)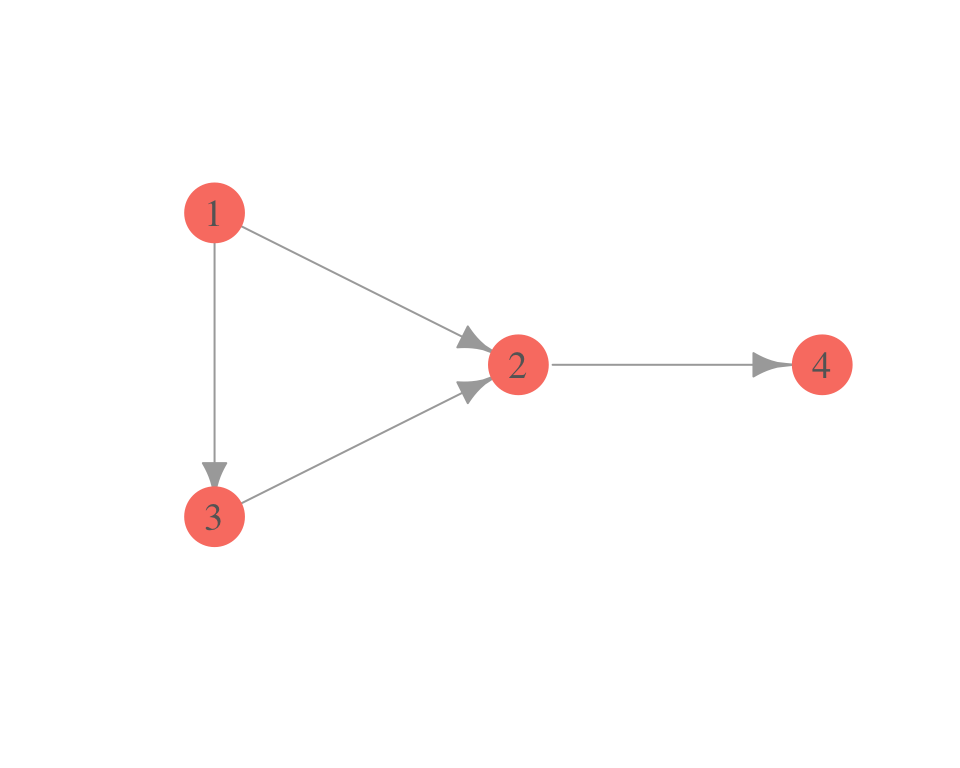
Ejemplo: Gráficas cíclicas. Cuando hay ciclos en una gráfica, no hay una manera clara de entender qué factorización produce. Por ejemplo, si tenemos tres variables , , asociados con un ciclo , esto quizá sugiere una factorización . Pero se puede ver que esta expresión en general no es una distribución de probabilidad.
# x: inteligencia, y: examen, z: trabajo
# y|x
mar_1 <- expand.grid(x = c("i_0", "i_1"), y = c("e_0", "e_1"))
mar_1$p1 <- c(0.95, 0.2, 0.05, 0.8)
# z|y
mar_2 <- expand.grid(y = c("e_0", "e_1"), z = c("t_0", "t_1"))
mar_2$p2 <- c(0.8, 0.4, 0.2, 0.6)
# x|z
mar_3 <- expand.grid(z = c("t_0", "t_1"), x = c("i_0", "i_1"))
mar_3$p3 <- c(0.8, 0.4, 0.2, 0.6)
tab_1 <- inner_join(mar_1, mar_2)
#> Joining, by = "y"
tab_2 <- inner_join(tab_1, mar_3)
#> Joining, by = c("x", "z")
tab_2$p <- tab_2$p1 * tab_2$p2 * tab_2$p3
sum(tab_2$p)
#> [1] 1.12En el ejemplo anterior vemos que no suma uno. Por otra parte si suma uno:
# x: inteligencia, y: examen, z: trabajo
# x
mar_1 <- data.frame(x = c("i_0", "i_1"), p1 = c(0.6, 0.4))
# y|x
mar_2 <- expand.grid(x = c("i_0", "i_1"), y = c("e_0", "e_1"))
mar_2$p2 <- c(0.95, 0.2, 0.05, 0.8)
# z|x,y
mar_3 <- expand.grid(y = c("e_0", "e_1"), x = c("i_0", "i_1"),
z = c("t_0", "t_1"))
mar_3$p3 <- c(0.8, 0.6, 0.5, 0.1, 0.2, 0.4, 0.5, 0.9)
tab_1 <- inner_join(mar_1, mar_2)
#> Joining, by = "x"
tab_2 <- inner_join(tab_1, mar_3)
#> Joining, by = c("x", "y")
tab_2$p <- tab_2$p1 * tab_2$p2 * tab_2$p3
sum(tab_2$p)
#> [1] 1