6.2 Variables latentes
Un caso importante de datos faltantes es cuando una variable está totalmente censurada. Esto puede suceder por dos razones:
Alguna variable claramente importante está totalmente censurada (por ejemplo, peso en un estudio de consumo de calorías).
Cuando buscamos añadir estructura a nuestro modelo para simplificar su estimación, interpretación o forma. Por ejemplo: hacer grupos de actitudes ante la comida y el ejercicio para explicar con una sola variable el consumo de comida chatarra (por ejemplo, análisis de factores).
En estos casos, estas variables se llaman variables latentes, pues consideramos que tienen un efecto que observamos a través de otras variables, pero no podemos observar directamente los valores de esta variable.
 ¿Cuál es el supuesto apropiado acerca
de este tipo de valores censurados (variables latentes)?
¿Cuál es el supuesto apropiado acerca
de este tipo de valores censurados (variables latentes)?
- MCAR
- MAR
- MNAR
- Ninguno de estos
La siguiente tabla es una clasificación de los modelos de variable latente de acuerdo a la métrica de las variables latentes y observadas.
| Latentes/Observadas | Métricas | Categóricas |
|---|---|---|
| Métricas | Análisis de factores (FA) | Modelos de rasgos latentes (LTM) |
| Categóricas | Modelos de perfiles latentes (LPM) | Modelos de clases latentes (LCM) |
6.2.1 Modelos de perfiles latentes: Mezcla de normales
El ejemplo más clásico de variables latentes es el de mezcla de normales.
Ejemplo. Modelo de mezcla de dos normales. Consideremos los siguientes datos:
library(ggplot2)
set.seed(280572)
N <- 800
n <- sum(rbinom(N, 1, 0.6))
x_1 <- rnorm(N - n, 0, 0.5)
x_2 <- rnorm(n, 2, 0.3)
qplot(c(x_1, x_2))
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.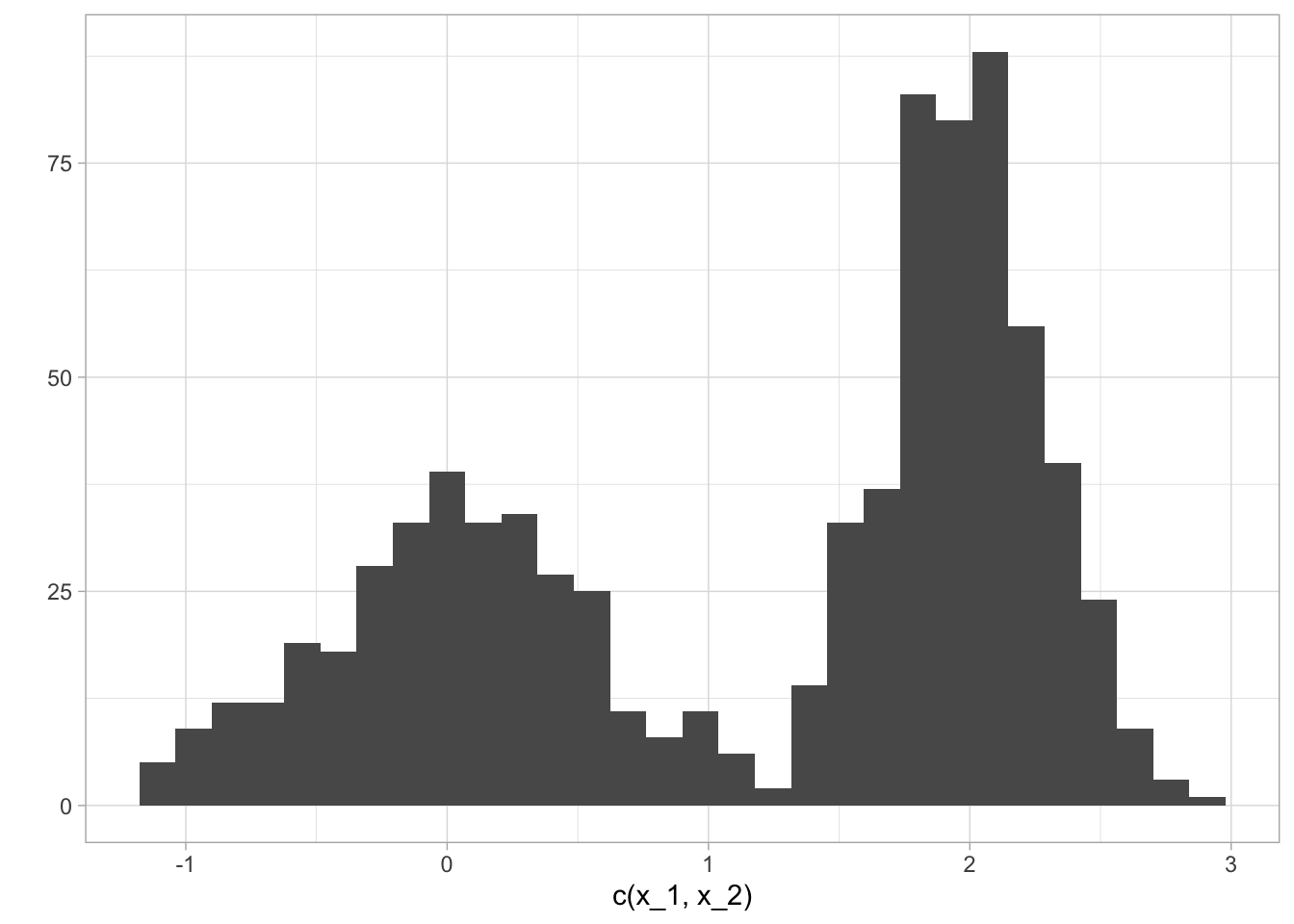
Estos datos tienen una estructura bimodal. Es poco apropiado modelar estos datos con un modelo normal \((\mu,\sigma^2)\).
Podemos entonces modelar pensando que los datos vienen de dos clases, cada una con una distribución normal pero con distintos parámetros. ¿Cómo ajustaríamos tal modelo?
La variable aleatoria \(X\) es una mezcla de normales si \[p(x)=\sum_{k=1}^K \pi_k \phi_{\theta_k}(x)\] donde \(\phi_{\theta_k}\) es una densidad normal con parámetros \(\theta_k=(\mu_k, \sigma_k)\) y los ponderadores de la mezcla \(\pi_k\) satisfacen \(\sum_i \pi_i = 1\)
Ahora, si vemos la mezcla Gaussiana desde la representación generativa, o formulación en variable latente, tenemos el modelo gráfico \(\Delta\) -> \(X\) donde \(\Delta\) es una indicadora de clase. En el caso del modelo de dos clases tenemos \(\delta \in \{0,1\}\) y sea \(P(\delta=1)=\pi\), escribimos la conjunta \[p(\delta, x)=\pi^{\delta}(1-\pi)^{1-\delta}[\delta\phi_{\theta_1}(x)+(1-\delta)\phi_{\theta_2}(x)]\]
y podemos verificar que la distribución marginal es una mezcla gaussiana: \[p(x)\sum_{\delta}p(x|\delta)p(\delta)\] \[=\phi_{\theta_1}(x) \pi + \phi_{\theta_2}(x)(1-\pi)\]
Ahora, si conocieramos la clase a la que pertenece cada observación (\(\delta^i\)) podríamos escribir la log-verosimilitud completa (sin censura) como \[\sum_{i=1}^N \log(\delta^i \phi_{\theta_1} (x^i)+ (1-\delta^i)\phi_{\theta_2}(x^i)) + \delta^i \log\pi + (1-\delta^i)\log(1-\pi).\]
Aquí, es fácil ver que la verosimilitud se separa en dos partes, una para \(\delta^i=1\) y otra para \(\delta^i=0\), y los estimadores de máxima verosimilitud son entonces:
\[\hat{\mu}_1=\frac{\sum_i\delta^i x^i}{\sum_i (\delta^i)}\] \[\hat{\mu}_2=\frac{\sum_i(1-\delta^i) x^i}{\sum_i (1-\delta^i)}\]
\[\hat{\sigma}_1^2=\frac{\sum_i\delta^i (x^i-\mu_1)^2}{\sum_i (\delta^i)}\] \[\hat{\sigma}_2^2=\frac{\sum_i(1-\delta^i) (x^i-\mu_2)^2}{\sum_i (1-\delta^i)},\]
y \(\hat{\pi}\) es la proporción de casos tipo 1 en los datos. Este problema es entonces trivial de resolver.
En el caso de variables latentes \(\delta^i\) están censuradas y tenemos que marginalizar con respecto a \(\delta^i\), resultando en:
\[\sum_{i=1}^N \log(\pi \phi_{\theta_1} (x^i)+ (1-\pi)\phi_{\theta_2}(x^i)).\]
donde \(\pi\) es la probabilidad de que la observación venga de la primera densidad. Este problema es más difícil pues tenemos tanto \(\pi\) como \(\theta_1\) y \(\theta_2\) dentro del logaritmo. Podemos resolver numéricamente como sigue:
crearLogLike <- function(x){
logLike <- function(theta){
pi <- exp(theta[1]) / (1 + exp(theta[1]))
mu_1 <- theta[2]
mu_2 <- theta[3]
sigma_1 <- exp(theta[4])
sigma_2 <- exp(theta[5])
sum(log(pi*dnorm(x, mu_1, sd=sigma_1)+(1-pi)*dnorm(x,mu_2,sd=sigma_2)))
}
logLike
}
func_1 <- crearLogLike(c(x_1,x_2))
system.time(salida <- optim(c(0.5,0,0,1,1), func_1, control=list(fnscale=-1)))
#> user system elapsed
#> 0.026 0.001 0.027
salida$convergence
#> [1] 0
exp(salida$par[1]) / (1 + exp(salida$par[1]))
#> [1] 0.5857074
salida$par[2:3]
#> [1] 1.98759218 0.03046366
exp(salida$par[4:5])
#> [1] 0.2977028 0.5159818Y vemos que hemos podido recuperar los parámetros originales.
Ahora implementamos EM para resolver este problema. Empezamos con la log-verosimilitud para datos completos (que reescribimos de manera más conveniente): \[\sum_{i=1}^N \delta^i\log\phi_{\theta_1} (x^i)+ (1-\delta^i)\log\phi_{\theta_2}(x^i) + \delta^i \log\pi + (1-\delta^i)\log(1-\pi).\]
Tomamos valores iniciales para los parámetros \(\hat{\mu}_1,\hat{\mu}_2,\hat{\sigma}_1^2, \hat{\sigma}_2^2, \hat{\pi}\) y comenzamos con el paso Esperanza promediando sobre las variables aleatorias, que en este caso son las \(\delta^i\). Calculamos entonces \[\hat{\gamma}^i=E_{\hat{\theta}}(\delta^i|x^i)=P(\delta^i=1|x^i),\] y usamos bayes para expresar en términos de los parámetros: \[\hat{\gamma}^i= \frac{\hat{\pi}\phi_{\hat{\theta_1}}} {\hat{\pi}\phi_{\hat{\theta_1}}(x_i)+(1-\hat{\pi})\phi_{\hat{\theta_2}}(x_i)}\]
\(\hat{\gamma}^i\) se conocen como la responsabilidad del modelo 1 para explicar la i-ésima observación.
Utilizando estas asignaciones de los faltantes pasamos al paso Maximización, donde la función objetivo es: \[\sum_{i=1}^N \hat{\gamma}^i\log \phi_{\theta_1} (x^i)+ (1-\hat{\gamma}^i)\log\phi_{\theta_2}(x^i) + \hat{\gamma}^i \log\pi + (1-\hat{\gamma}^i)\log(1-\pi).\]
La actualización de \(\pi\) es fácil:
\[\hat{\pi}=\frac{1}{N}\sum_i{\gamma^i}.\]
y se puede ver sin mucha dificultad que
\[\hat{\mu}_1=\frac{\sum_i\hat{\gamma}^i x^i}{\sum_i \hat{\gamma}^i}\] \[\hat{\mu}_2=\frac{\sum_i(1-\hat{\gamma}^i) x^i}{\sum_i (1-\hat{\gamma}^i})\]
\[\hat{\sigma}_1^2=\frac{\sum_i\hat{\gamma}^i (x^i-\mu_1)^2}{\sum_i \hat{\gamma}^i}\] \[\hat{\sigma}_2^2=\frac{\sum_i(1-\hat{\gamma}^i) (x^i-\mu_2)^2}{\sum_i (1-\hat{\gamma}^i)},\]
 Implementa EM para el ejemplo de
mezcla de normales.
Implementa EM para el ejemplo de
mezcla de normales.