2.3 Modelos locales
En esta parte veremos cómo construir los modelos locales que corresponden a factores en la regla del producto para factorizaciones sobre DAGs, y veremos cómo usar datos para ajustar sus parámetros.
2.3.1 Tablas de probabilidad condicional
En primer lugar, recordemos que siempre podemos hacer representaciones tabulares para la condicional de cada variable dado sus padres: \[P(X|Pa(X)),\] donde establecemos, para cada combinación de valores de las variables en \(Pa(X)\), una distribución sobre \(X\) tal que \[\sum_x P(X=x|Pa(X))=1.\]
Ejemplo. En el ejemplo de la clase anterior construimos directamente las condicionales de llueve (no condicional), regar (no condicional) y mojado dado llueve y regar:
llueve <- c('Sí','No')
regar <- c('Prendido', 'Apagado')
p_llueve <- data.frame(llueve = llueve, prob.l = c(0.1, 0.9))
p_llueve
#> llueve prob.l
#> 1 Sí 0.1
#> 2 No 0.9
p_regar <- data.frame(regar = regar, prob.r = c(0.2, 0.8))
p_regar
#> regar prob.r
#> 1 Prendido 0.2
#> 2 Apagado 0.8
mojado <- c('Mojado','Seco')
niveles <- expand.grid(llueve = llueve, regar = regar, mojado = mojado)
p_mojado_lr <- data.frame(niveles, prob_m = NA)
p_mojado_lr$prob_m[1:4] <- c(0.97, 0.9, 0.8, 0.01)
p_mojado_lr$prob_m[5:8]<- 1 - p_mojado_lr$prob_m[1:4]
p_mojado_lr
#> llueve regar mojado prob_m
#> 1 Sí Prendido Mojado 0.97
#> 2 No Prendido Mojado 0.90
#> 3 Sí Apagado Mojado 0.80
#> 4 No Apagado Mojado 0.01
#> 5 Sí Prendido Seco 0.03
#> 6 No Prendido Seco 0.10
#> 7 Sí Apagado Seco 0.20
#> 8 No Apagado Seco 0.99Representar los modelos locales de esta forma tiene una desventaja potencial: Esta representación no explota ninguna regularidad que pueda existir en la condicional, así que cuando la variable respuesta depende de muchas variables hay muchos parámetros por estimar individualmente (cada probabilidad condicional, menos uno). Esto puede ser difícil de ajustar con datos o demasiado engorroso de elicitar para un experto.
Ejemplos de regularidades:
- Si riegan, entonces el piso va a estar mojado sin importar si llueve o no. (no es necesario un parámetro separado para llueve/no llueve)
- La probabilidad de conseguir ser aceptado en una universidad depende de la calidad de las cartas de recomendación del profesor A, el profesor B, y de la carta que decida enviar el solicitante. Si un estudiante escoge la carta de recomendación del profesor A para pedir trabajo, la probabilidad de conseguir el trabajo no depende de la carta del profesor B. (dado que escogió la carta A, basta dar la tabla de probabilidades aceptación-calidad de carta A, sin importar la calidad de la carta B).
- La probabilidad de una categoría sigue un modelo logístico sin interacciones entre las variables de entrada (padres) (no es necesario tener parámetros para interacciones entre las variables de entrada).
En todos estos casos, podemos reducir el número de parámetros a estimar y obtener una representación más simple, siempre y cuando nuestros modelos más simples ajusten a los datos.
La idea importante es que para especificar las probabilidades condicionales no es necesario dar una tabla completa explícitamente. Podemos tener reglas o modelos simples de las cuales podamos calcular cualquier probabilidad condicional que nos interese.
2.3.2 Estimación directa por máxima verosimilitud
Cuando usamos datos para estimar los modelos locales, si no hacemos supuestos sobre la estructura de los modelos locales, podemos usar máxima verosimilitud para hacer la estimación.
Para estimar \[P(X_i=x|X_1=x_1,\ldots, X_k=x_k)\]
utilizamos simplemente \[\frac{N(X_i=x,X_1=x_1,\ldots, X_k=x_k)}{N(X_1=x_1,\ldots, X_k=x_k)}.\]
Nótese que cuando hay muchas variables de entrada/relativamente pocos datos, esta estimación puede ser muy ruidosa (pocos casos en el denominador), o simplemente infactible. Para modelos simples funciona razonablemente bien.
Una solución (relacionada con un modelo bayesiano) es suavizar los conteos con \[\frac{N(X_i=x,X_1=x_1,\ldots, X_k=x_k)+\alpha_x}{N(X_1=x_1,\ldots, X_k=x_k)+\alpha},\] donde \(\sum_x \alpha_x=\alpha\).
Ejemplo. Consideramos el siguiente ejemplo de datos de la ENIGH 2010 (una observación por hogar, características de hogares y sus habitantes):
library(bnlearn)
library(plyr)
#> -------------------------------------------------------------------------
#> You have loaded plyr after dplyr - this is likely to cause problems.
#> If you need functions from both plyr and dplyr, please load plyr first, then dplyr:
#> library(plyr); library(dplyr)
#> -------------------------------------------------------------------------
#>
#> Attaching package: 'plyr'
#> The following objects are masked from 'package:dplyr':
#>
#> arrange, count, desc, failwith, id, mutate, rename, summarise,
#> summarize
#> The following object is masked from 'package:purrr':
#>
#> compact
library(dplyr)
load(file = 'data/dat_ing.Rdata')
dat_ing$marg <- factor(as.character(dat_ing$marg))
# creamos una base únicamente con variables de interés
dat_ing_f <- dplyr::select(dat_ing, tam_loc, marg, decil, nivelaprob, vehiculo,
drenaje, pisos, sexojefe)
black <- data.frame(
form = c('drenaje', 'nivelaprob', 'decil', 'decil', 'nivelaprob'),
to = c('decil', 'sexojefe', 'nivelaprob', 'tam_loc', 'marg'))
net_enigh <- hc(dat_ing_f, score = 'aic', blacklist = black)
net_enigh
#>
#> Bayesian network learned via Score-based methods
#>
#> model:
#> [tam_loc][marg|tam_loc][sexojefe|tam_loc]
#> [nivelaprob|tam_loc:marg:sexojefe][decil|marg:nivelaprob]
#> [vehiculo|decil:nivelaprob:sexojefe][drenaje|tam_loc:marg:decil]
#> [pisos|decil:drenaje]
#> nodes: 8
#> arcs: 15
#> undirected arcs: 0
#> directed arcs: 15
#> average markov blanket size: 4.50
#> average neighbourhood size: 3.75
#> average branching factor: 1.88
#>
#> learning algorithm: Hill-Climbing
#> score: AIC (disc.)
#> penalization coefficient: 1
#> tests used in the learning procedure: 126
#> optimized: TRUE
fit_enigh_mle <- bn.fit(net_enigh, data = dat_ing_f, method = 'mle')
#write.net("./salidas/enigh_mle_1.net", fit_enigh_mle)
graphviz.plot(net_enigh)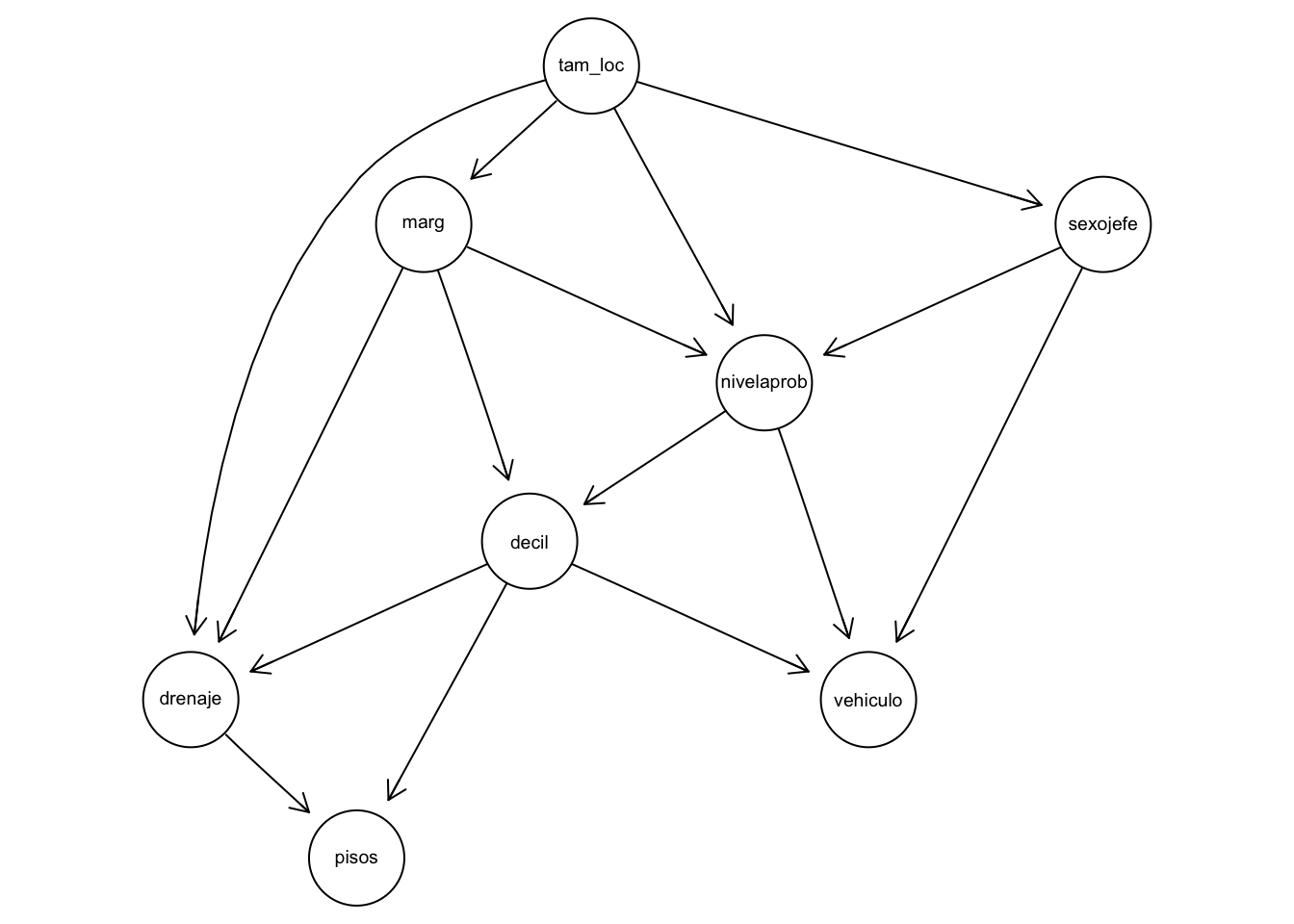
La estimación por máxima verosimilitud para la condicional de marginación dado tamaño de localidad es
fit_enigh_mle[['marg']]
#>
#> Parameters of node marg (multinomial distribution)
#>
#> Conditional probability table:
#>
#> tam_loc
#> marg 100 mil o mas De 15 mil a 100 mil De 2500 a 15 mil
#> Alto 0.00000000 0.14987332 0.29328724
#> Bajo 0.06997547 0.29156110 0.22875252
#> Medio 0.03715193 0.20093549 0.23624316
#> Muy alto 0.00000000 0.02338725 0.09248055
#> Muy bajo 0.89287260 0.33424284 0.14923653
#> tam_loc
#> marg Menos de 2500
#> Alto 0.31547619
#> Bajo 0.14271196
#> Medio 0.21370499
#> Muy alto 0.21864111
#> Muy bajo 0.10946574Que es simplemente (máxima verosimilitud):
tab_1 <- table(dat_ing$marg, dat_ing$tam_loc)
tab_1
#>
#> 100 mil o mas De 15 mil a 100 mil De 2500 a 15 mil
#> Alto 0 769 1018
#> Bajo 970 1496 794
#> Medio 515 1031 820
#> Muy alto 0 120 321
#> Muy bajo 12377 1715 518
#>
#> Menos de 2500
#> Alto 2173
#> Bajo 983
#> Medio 1472
#> Muy alto 1506
#> Muy bajo 754
tab_2 <- prop.table(tab_1, margin = 2)
tab_2
#>
#> 100 mil o mas De 15 mil a 100 mil De 2500 a 15 mil
#> Alto 0.00000000 0.14987332 0.29328724
#> Bajo 0.06997547 0.29156110 0.22875252
#> Medio 0.03715193 0.20093549 0.23624316
#> Muy alto 0.00000000 0.02338725 0.09248055
#> Muy bajo 0.89287260 0.33424284 0.14923653
#>
#> Menos de 2500
#> Alto 0.31547619
#> Bajo 0.14271196
#> Medio 0.21370499
#> Muy alto 0.21864111
#> Muy bajo 0.10946574En este ejemplo, donde los denominadores son relativamente grandes, no es necesario hacer ningún suavizamiento. Sin embargo, podemos utilizar suavizamiento de conteos de la siguiente forma (iss es imaginary sample size).
fit_enigh_b <- bn.fit(net_enigh, data = dat_ing_f, method = 'bayes', iss = 100)
fit_enigh_b[['marg']]
#>
#> Parameters of node marg (multinomial distribution)
#>
#> Conditional probability table:
#>
#> tam_loc
#> marg 100 mil o mas De 15 mil a 100 mil De 2500 a 15 mil
#> Alto 0.000360049 0.150116369 0.292620137
#> Bajo 0.070209548 0.291117145 0.228546911
#> Medio 0.037445093 0.200930954 0.235983982
#> Muy alto 0.000360049 0.024243600 0.093249428
#> Muy bajo 0.891625261 0.333591932 0.149599542
#> tam_loc
#> marg Menos de 2500
#> Alto 0.315058585
#> Bajo 0.142919138
#> Medio 0.213655432
#> Muy alto 0.218573702
#> Muy bajo 0.109793143
prop.table(tab_1 + 100 / (4 * 5), margin = 2)
#>
#> 100 mil o mas De 15 mil a 100 mil De 2500 a 15 mil
#> Alto 0.000360049 0.150116369 0.292620137
#> Bajo 0.070209548 0.291117145 0.228546911
#> Medio 0.037445093 0.200930954 0.235983982
#> Muy alto 0.000360049 0.024243600 0.093249428
#> Muy bajo 0.891625261 0.333591932 0.149599542
#>
#> Menos de 2500
#> Alto 0.315058585
#> Bajo 0.142919138
#> Medio 0.213655432
#> Muy alto 0.218573702
#> Muy bajo 0.109793143Mayor suavizamiento regulariza más los conteos. Para muestras más chicas, es posible que sea necesario escoger suavizamientos más chicos.
Ejemplo. Repetiremos el ejercicio con una muestra chica para ver cómo puede mejorar nuestra estimación el suavizamiento.
set.seed(282095)
# tomamos una muestra de tamaño 50
dat_ing_muestra <- sample_n(dat_ing_f, 50)
# veamos la tabla cruda
table(dat_ing_muestra$marg, dat_ing_muestra$tam_loc)
#>
#> 100 mil o mas De 15 mil a 100 mil De 2500 a 15 mil
#> Alto 0 1 3
#> Bajo 1 4 1
#> Medio 0 1 2
#> Muy alto 0 0 1
#> Muy bajo 20 6 1
#>
#> Menos de 2500
#> Alto 4
#> Bajo 1
#> Medio 1
#> Muy alto 0
#> Muy bajo 3
# usamos máxima verosimilitud
fit_enigh_1 <- bn.fit(net_enigh, data = dat_ing_muestra, method='mle')
probs_est_mle <- data.frame(fit_enigh_1[['marg']]$prob)
names(probs_est_mle)[3] <- 'mle'
probs_est_mle
#> marg tam_loc mle
#> 1 Alto 100 mil o mas 0.00000000
#> 2 Bajo 100 mil o mas 0.04761905
#> 3 Medio 100 mil o mas 0.00000000
#> 4 Muy alto 100 mil o mas 0.00000000
#> 5 Muy bajo 100 mil o mas 0.95238095
#> 6 Alto De 15 mil a 100 mil 0.08333333
#> 7 Bajo De 15 mil a 100 mil 0.33333333
#> 8 Medio De 15 mil a 100 mil 0.08333333
#> 9 Muy alto De 15 mil a 100 mil 0.00000000
#> 10 Muy bajo De 15 mil a 100 mil 0.50000000
#> 11 Alto De 2500 a 15 mil 0.37500000
#> 12 Bajo De 2500 a 15 mil 0.12500000
#> 13 Medio De 2500 a 15 mil 0.25000000
#> 14 Muy alto De 2500 a 15 mil 0.12500000
#> 15 Muy bajo De 2500 a 15 mil 0.12500000
#> 16 Alto Menos de 2500 0.44444444
#> 17 Bajo Menos de 2500 0.11111111
#> 18 Medio Menos de 2500 0.11111111
#> 19 Muy alto Menos de 2500 0.00000000
#> 20 Muy bajo Menos de 2500 0.33333333
# repetimos con suavizamiento
fit_enigh_2 <- bn.fit(net_enigh, data = dat_ing_muestra, method = 'bayes',
iss = 30)
probs_est_bayes <- data.frame(fit_enigh_2[['marg']]$prob)
names(probs_est_bayes)[3] <- 'bayes'
probs_1 <- join(probs_est_mle, probs_est_bayes)
#> Joining by: marg, tam_loc
# comparamos con las estimaciones que toman toda la base
tab_df <- data.frame(tab_2)
names(tab_df) <- c('marg', 'tam_loc', 'mle_c')
# las unimos a la base de datos probs_1
probs_2 <- join(probs_1, tab_df)
#> Joining by: marg, tam_loc
# creamos dos nuevas variables: método y estimación para poder graficar
probs_2_l <- gather(probs_2, metodo, est, mle, bayes, mle_c)
ggplot(probs_2_l, aes(x = marg, y = est, colour = metodo)) +
geom_jitter(size=3,position=position_jitter(width=0.1, height=0))+
facet_wrap(~ tam_loc)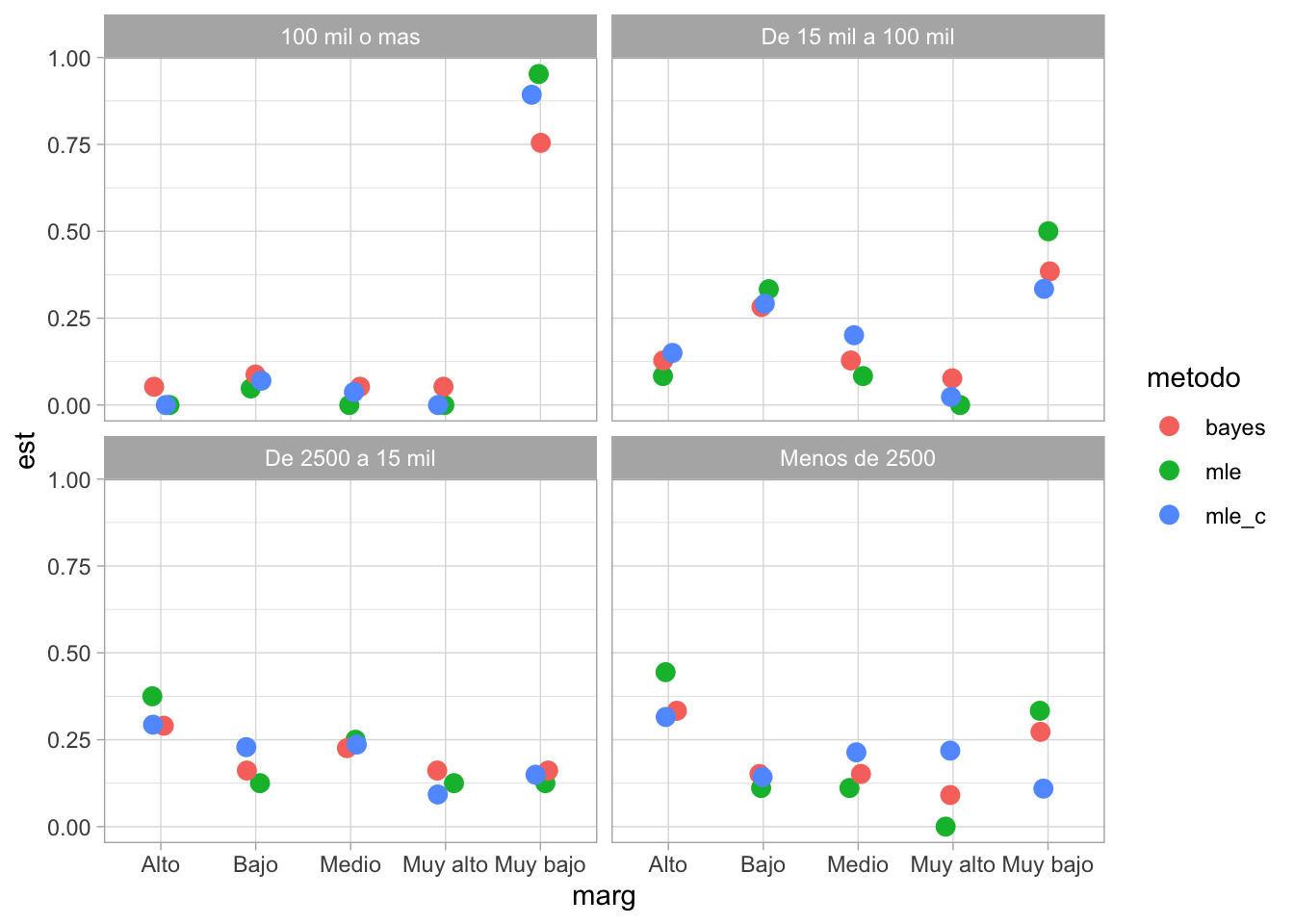
Muy poca regularización (iss chica) típicamente no tiene efectos negativos (y conviene hacerla para evitar estimación de ceros), pero puede ser que demasiada regularización sí. Este parámetro puede ser escogido mediante validación cruzada, o desde un punto de vista bayesiano con información previa.
Ejemplo. Cuando los modelos son más complejos, la estimación de máxima verosimilitud puede ser muy mala, por ejemplo:
mle_vehiculo <- data.frame(fit_enigh_mle[['vehiculo']]$prob)
mle_vehiculo_true <- filter(mle_vehiculo, vehiculo == 'TRUE',
nivelaprob!='No esp')
ggplot(mle_vehiculo_true, aes(x = nivelaprob, y = Freq, colour = decil,
group = decil)) +
facet_wrap(~ sexojefe) +
geom_point() +
geom_line() +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) 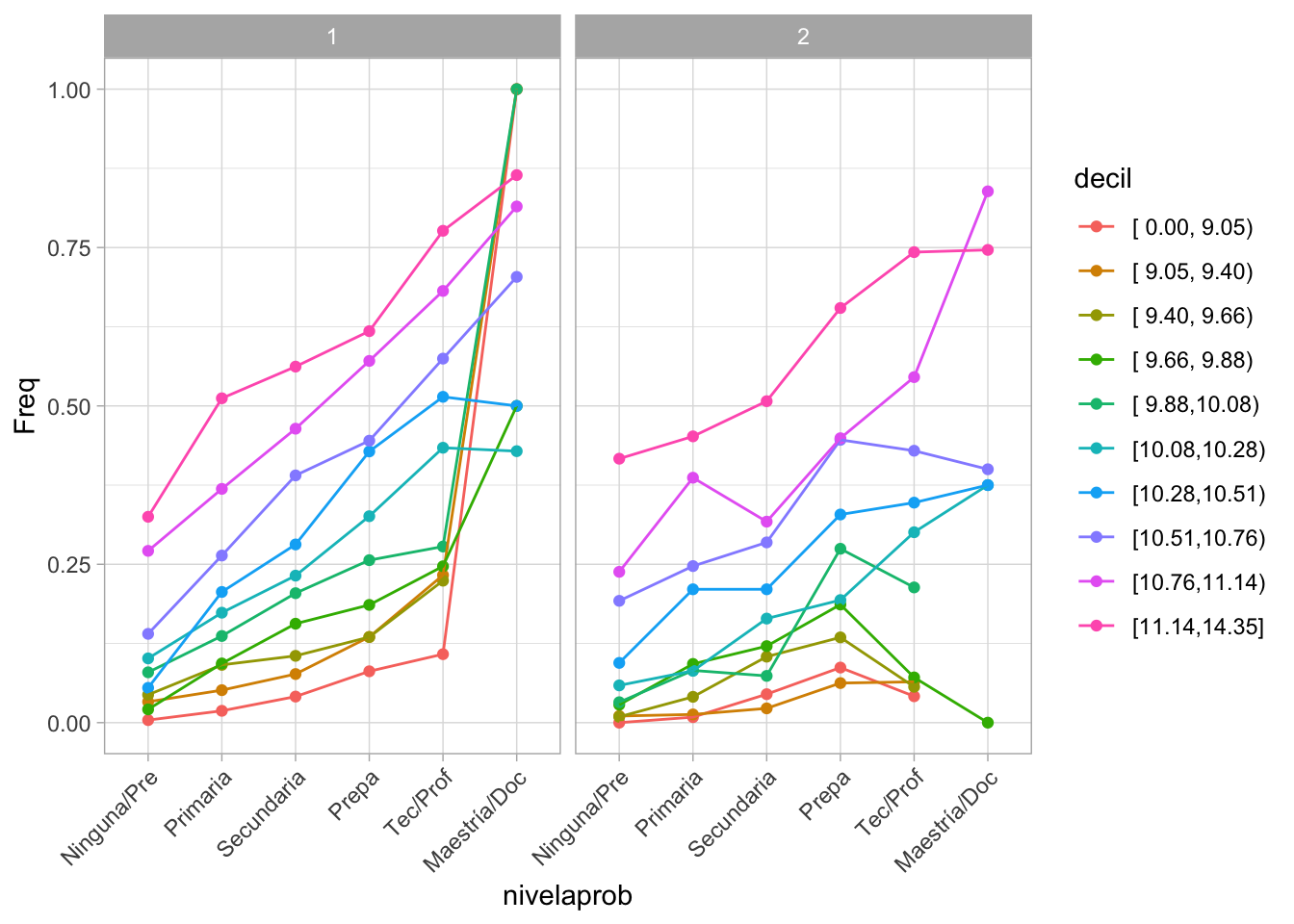
fit_enigh_b <- bn.fit(net_enigh, data = dat_ing_f, method = 'bayes', iss = 1000)
b_vehiculo <- data.frame(fit_enigh_b[['vehiculo']]$prob)
b_vehiculo_true <- filter(b_vehiculo, vehiculo == 'TRUE',
nivelaprob!='No esp')
ggplot(b_vehiculo_true, aes(x = nivelaprob, y = Freq, colour = decil,
group = decil)) +
facet_wrap(~ sexojefe) +
geom_point() +
geom_line() +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) 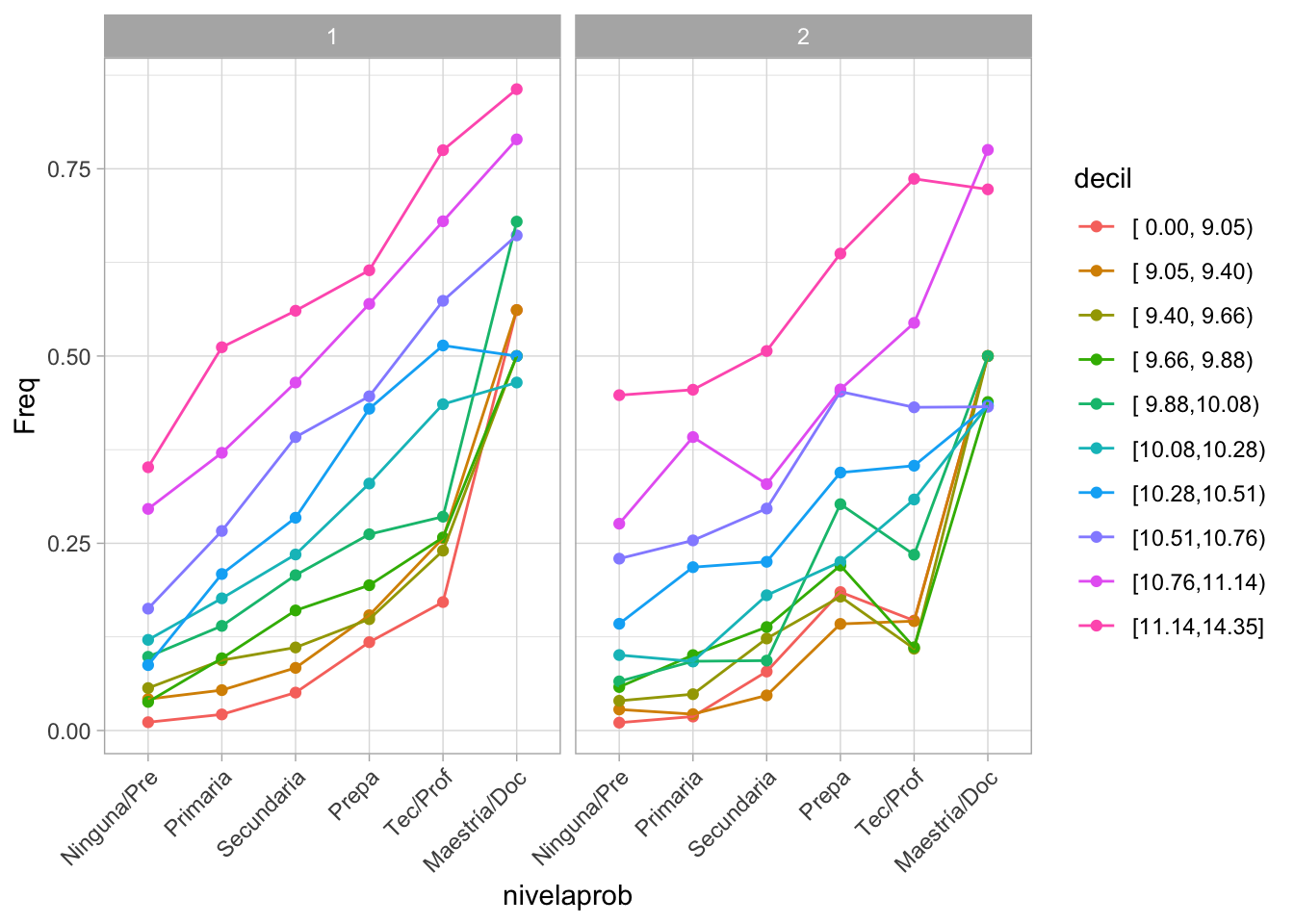
2.3.3 Probabilidades condicionales basadas en árboles
Podemos usar árboles de decisión para construir versiones compactas de probabilidades condicionales.
Ejemplo. Una carta de recomendación buena del profesor A da una probabilidad de 0.6 de conseguir el trabajo, mientras que una carta mala de 0.4. Para el profesor B, las probabilidades son 0.8 y 0.4. Consideramos la siguiente gráfica:
library(igraph)
gr <- graph(c(1, 2, 3, 2, 4, 2))
plot(gr,
vertex.label = c('ProfA', 'Trabajo', 'ProfB', 'Carta'),
layout = matrix(c(0, 1, 0.6, 0, 0,-1, 0, 0), byrow = TRUE, ncol = 2),
vertex.size = 20, vertex.color = 'salmon', vertex.label.cex = 1.2,
vertex.label.color = 'gray40', vertex.frame.color = NA, asp = 0.8,
edge.arrow.size = 1)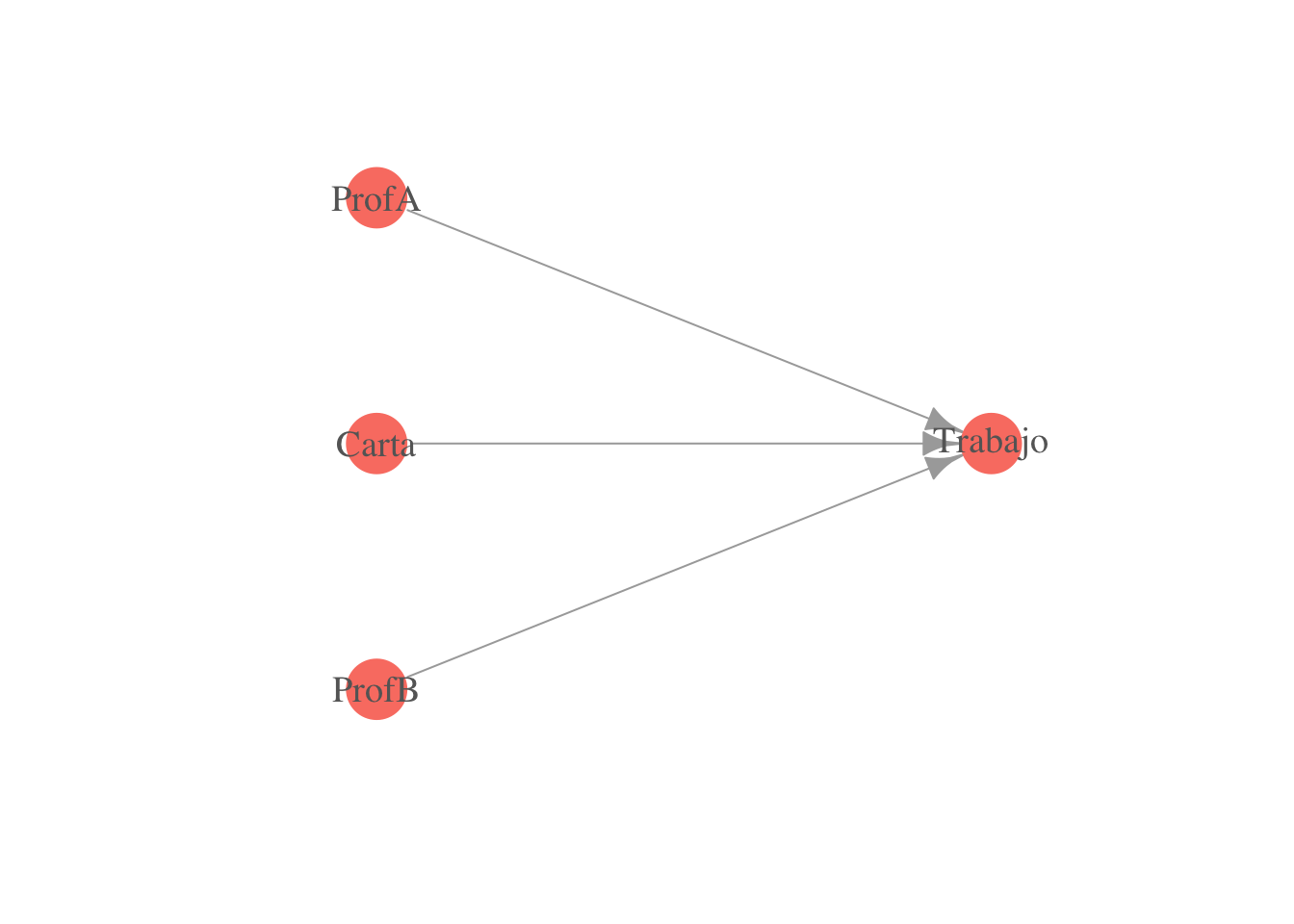
La tabla de probabilidad condicional correspondiente a Trabajo tiene un total de 8 parámetros. Sin embargo, por la observación anterior, en relidad está dada por 2 parámetros, pues Trabajo sólo depende de ProfA cuando Carta=A, y sólo depende de ProfB cuando Carta=B (con las mismas probabilidades 0.6 y 0.4).
Representamos este escenario mediante un árbol:

La estructura adicional que observamos es que cuando Carta=A, Trabajo es condicionalmente independiente de Prof B, y cuando Carta=B, Trabajo es condiconalmente independiente de ProfA. Esta es una independencia condicional distinta a las que vimos antes: dice que para ciertos niveles de alguna variable, existen independencias condicionales entre otras variables. Esto no quiere decir que dado Carta, Trabajo sea condicionalmente independiente de ProfA o ProfB. Otra manera de decir esto es que estos modelos locales pueden tener información de independencias condicionales en ciertos contextos (para valores particulares de las variables).
Ejemplo
library(rpart)
library(rpart.plot)
library(rattle)
#> Rattle: A free graphical interface for data science with R.
#> Version 5.2.0 Copyright (c) 2006-2018 Togaware Pty Ltd.
#> Type 'rattle()' to shake, rattle, and roll your data.
set.seed(22857)
# simulamos datos
prof_a <- sample(c('Buena', 'Mala', 'Mala'), 400, replace = T)
prof_b <- sample(c('Buena', 'Buena', 'Mala'), 400, replace = T)
carta <- sample(c('A', 'B'), 400, replace = T)
datos_sim <- data.frame(prof_a, prof_b, carta)
# describimos las probabilidades
probas <- datos_sim %>%
distinct() %>%
mutate(proba = (prof_a == 'Mala' & carta == 'A') * 0.4 +
(prof_b == 'Mala' & carta == 'B') * 0.4 +
(prof_a == 'Buena' & carta == 'A') * 0.6 +
(prof_b == 'Buena' & carta == 'B') * 0.8)
probas
#> prof_a prof_b carta proba
#> 1 Mala Mala B 0.4
#> 2 Mala Buena A 0.4
#> 3 Buena Buena B 0.8
#> 4 Buena Buena A 0.6
#> 5 Mala Buena B 0.8
#> 6 Mala Mala A 0.4
#> 7 Buena Mala B 0.4
#> 8 Buena Mala A 0.6
# finalmente simulamos si consigue el trabajo
datos_1 <- inner_join(datos_sim, probas)
#> Joining, by = c("prof_a", "prof_b", "carta")
datos_1$consigue <- rbinom(nrow(datos_1), size = 1, prob = datos_1$prob)
# usamos un árbol de decisión
arbol_1 <- rpart(consigue ~ prof_a + prof_b + carta, datos_1, method = 'class',
cp = 0)
printcp(arbol_1)
#>
#> Classification tree:
#> rpart(formula = consigue ~ prof_a + prof_b + carta, data = datos_1,
#> method = "class", cp = 0)
#>
#> Variables actually used in tree construction:
#> [1] carta prof_a prof_b
#>
#> Root node error: 190/400 = 0.475
#>
#> n= 400
#>
#> CP nsplit rel error xerror xstd
#> 1 0.215789 0 1.00000 1.00000 0.052566
#> 2 0.068421 1 0.78421 0.78421 0.050892
#> 3 0.057895 2 0.71579 0.80000 0.051093
#> 4 0.000000 3 0.65789 0.72632 0.050039
fancyRpartPlot(arbol_1)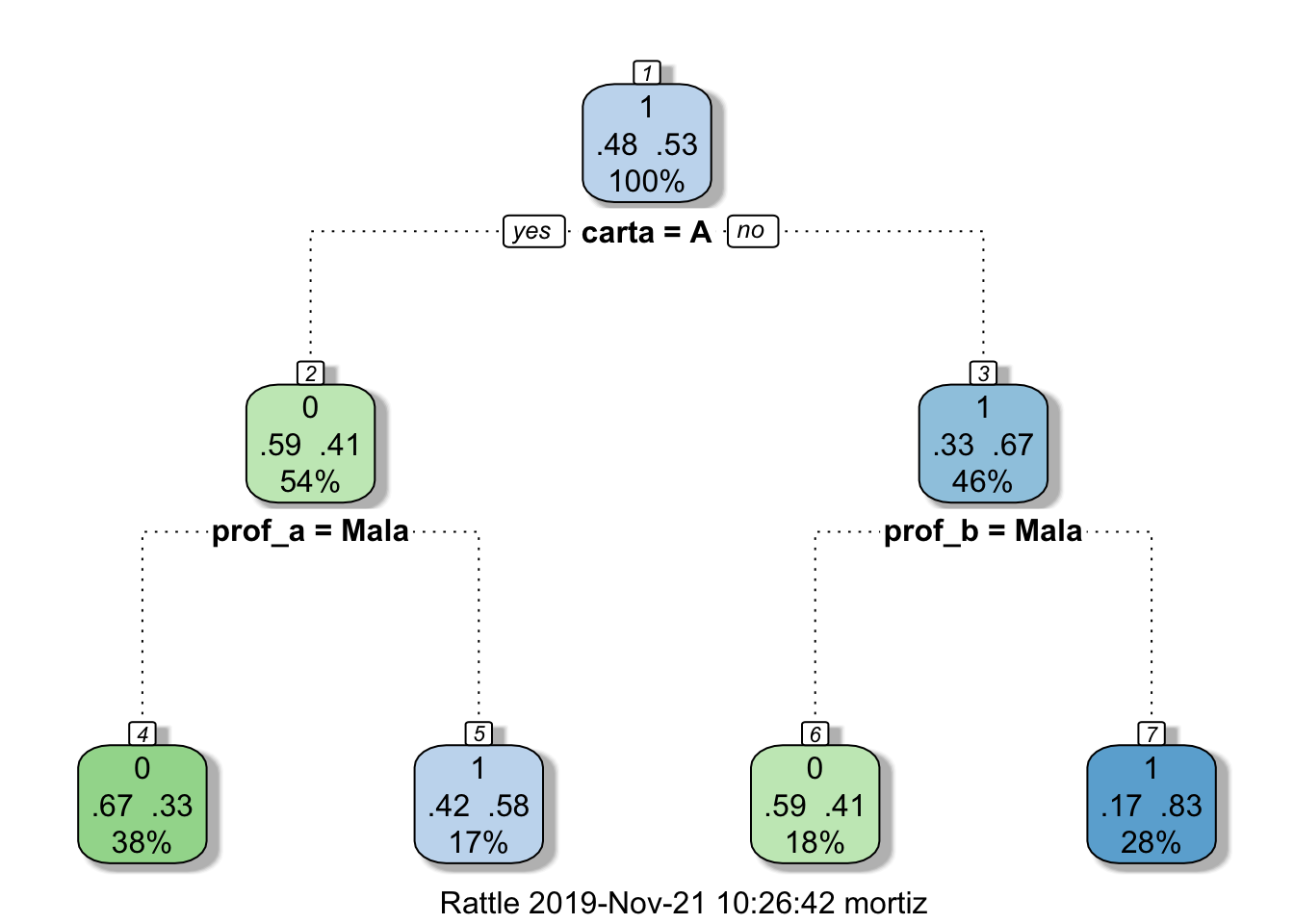
Aunque, sin más información, no hay garantía de recuperar la forma original.
set.seed(46654)
prof_a <- sample(c('Buena', 'Mala', 'Mala'), 300, replace = T)
prof_b <- sample(c('Buena', 'Buena', 'Mala'), 300, replace = T)
carta <- sample(c('A', 'B'), 300, replace = T)
datos_sim <- data.frame(prof_a, prof_b, carta)
# describimos las probabilidades
probas <- datos_sim %>%
distinct() %>%
mutate(proba = (prof_a == 'Mala' & carta == 'A') * 0.4 +
(prof_b == 'Mala' & carta == 'B') * 0.4 +
(prof_a == 'Buena' & carta == 'A') * 0.6 +
(prof_b == 'Buena' & carta == 'B') * 0.8)
# finalmente simulamos si consigue el trabajo
datos_1 <- inner_join(datos_sim, probas)
#> Joining, by = c("prof_a", "prof_b", "carta")
datos_1$consigue <- rbinom(nrow(datos_1), size = 1, prob = datos_1$prob)
# usamos un árbol de decisión
arbol_2 <- rpart(consigue ~ prof_a + prof_b + carta, datos_1, method = 'class',
cp = 0)
printcp(arbol_2)
#>
#> Classification tree:
#> rpart(formula = consigue ~ prof_a + prof_b + carta, data = datos_1,
#> method = "class", cp = 0)
#>
#> Variables actually used in tree construction:
#> [1] carta prof_a prof_b
#>
#> Root node error: 137/300 = 0.45667
#>
#> n= 300
#>
#> CP nsplit rel error xerror xstd
#> 1 0.1824818 0 1.00000 1.00000 0.062976
#> 2 0.0036496 1 0.81752 0.87591 0.061936
#> 3 0.0000000 3 0.81022 0.98540 0.062897
fancyRpartPlot(arbol_2)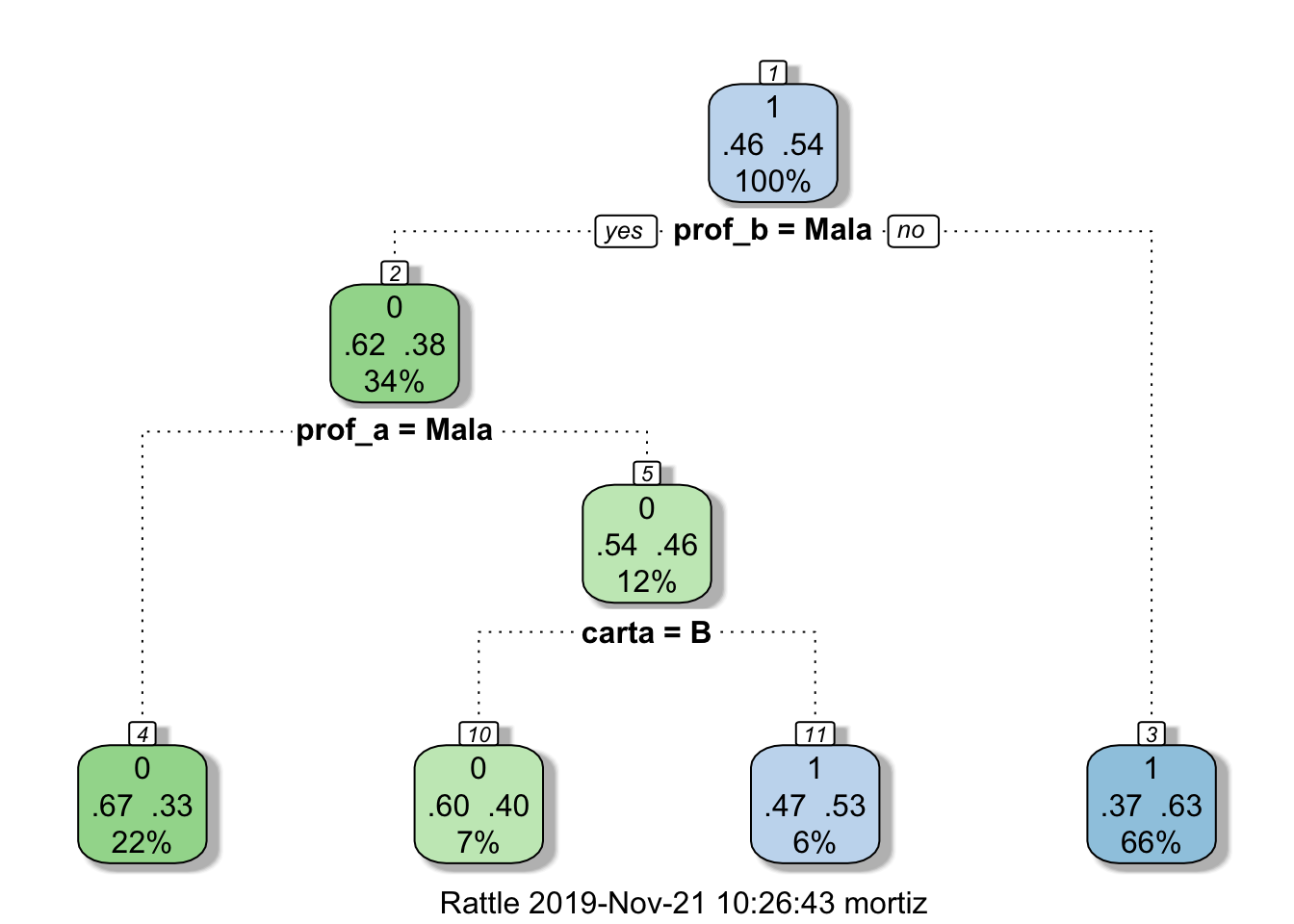
# usamos un árbol de decisión
arbol_3 <- rpart(consigue ~ prof_a + prof_b + carta, datos_1, method = 'class',
cp = 0, cost = c(100, 100, 1))
printcp(arbol_3)
#>
#> Classification tree:
#> rpart(formula = consigue ~ prof_a + prof_b + carta, data = datos_1,
#> method = "class", cost = c(100, 100, 1), cp = 0)
#>
#> Variables actually used in tree construction:
#> [1] carta prof_a prof_b
#>
#> Root node error: 137/300 = 0.45667
#>
#> n= 300
#>
#> CP nsplit rel error xerror xstd
#> 1 0.0802920 0 1.00000 1.00000 0.062976
#> 2 0.0218978 2 0.83942 0.90511 0.062257
#> 3 0.0072993 3 0.81752 0.95620 0.062704
#> 4 0.0000000 4 0.81022 0.95620 0.062704
fancyRpartPlot(arbol_3)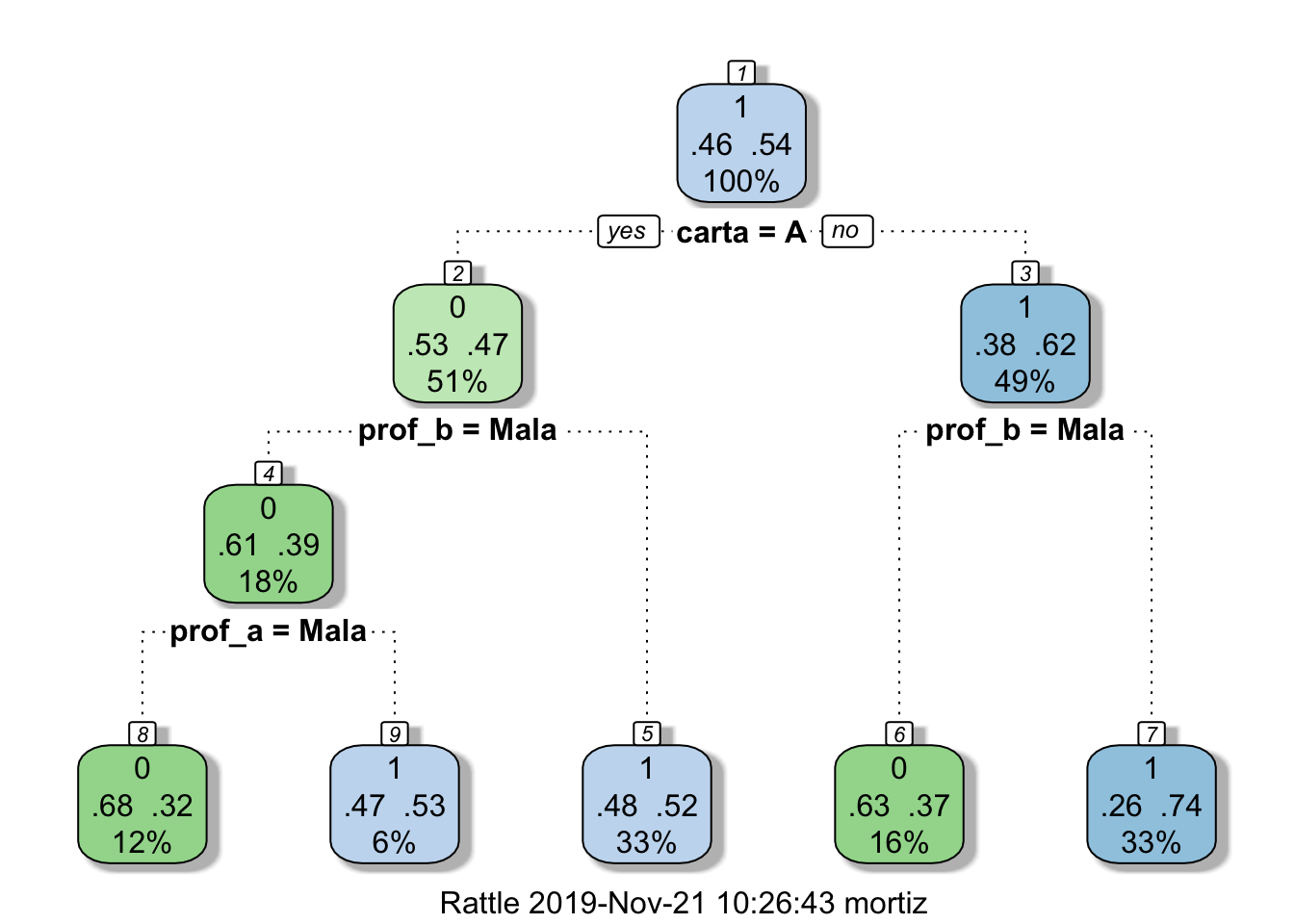
2.3.4 Modelos lineales generalizados
Otra técnica es utilizar modelos logísticos multinomiales (o simplemente logístico cuando la respuesta tiene 2 niveles). La ventaja de este enfoque es que podemos controlar la complejidad del modelo a través de inclusión/exclusión de interacciones y regularización.
net_enigh <- hc(dat_ing_f, score='aic', blacklist = black)
net_enigh
#>
#> Bayesian network learned via Score-based methods
#>
#> model:
#> [tam_loc][marg|tam_loc][sexojefe|tam_loc]
#> [nivelaprob|tam_loc:marg:sexojefe][decil|marg:nivelaprob]
#> [vehiculo|decil:nivelaprob:sexojefe][drenaje|tam_loc:marg:decil]
#> [pisos|decil:drenaje]
#> nodes: 8
#> arcs: 15
#> undirected arcs: 0
#> directed arcs: 15
#> average markov blanket size: 4.50
#> average neighbourhood size: 3.75
#> average branching factor: 1.88
#>
#> learning algorithm: Hill-Climbing
#> score: AIC (disc.)
#> penalization coefficient: 1
#> tests used in the learning procedure: 126
#> optimized: TRUE
fit_enigh <- bn.fit(net_enigh, data = dat_ing_f, method='mle')
graphviz.plot(net_enigh)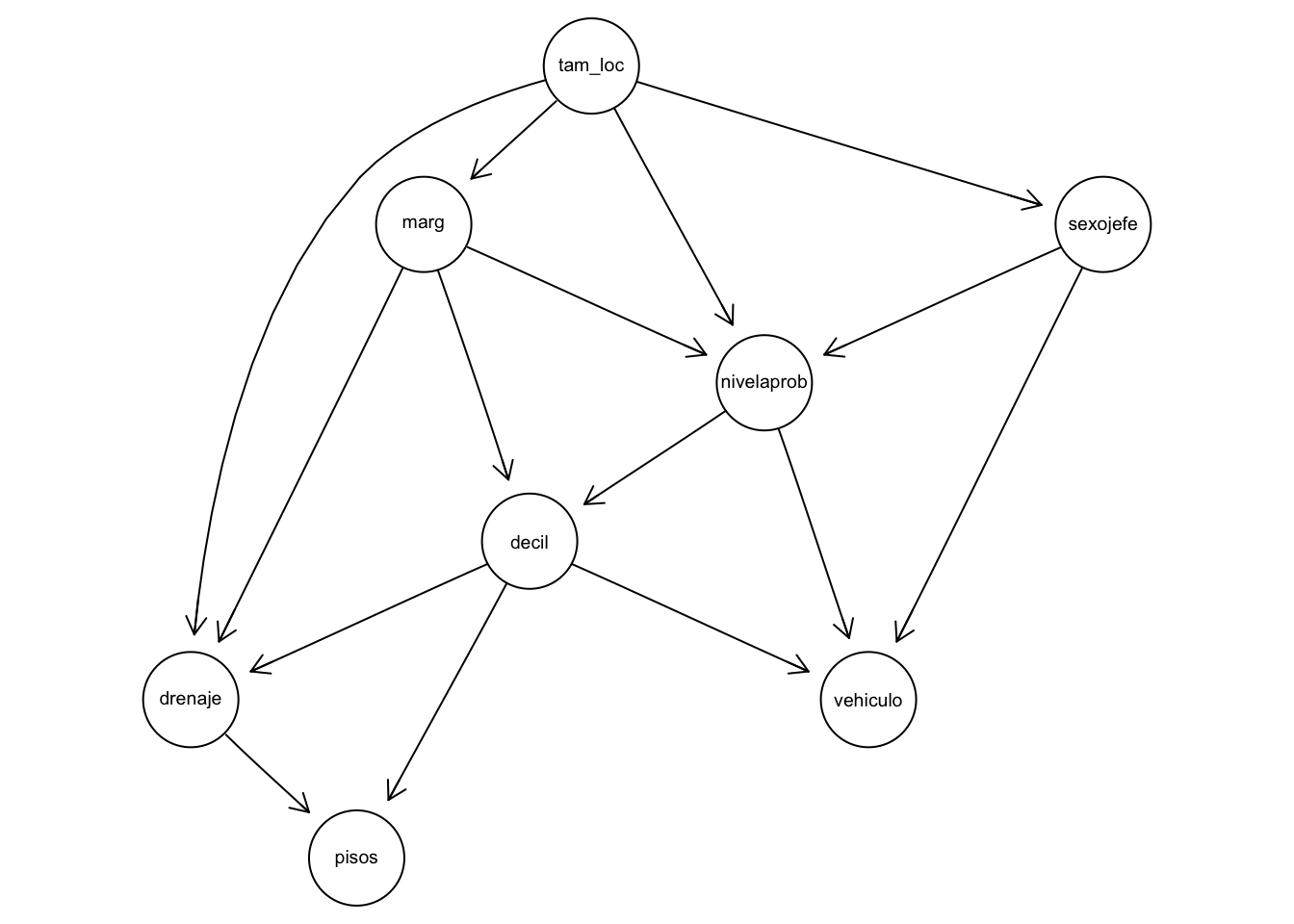
Nos interesa el nodo de posesión de vehículo dado decil, nivel aprobado del jefe de familia y sexo del jefe de familia. En este caso, utilizaremos un modelo logístico regularizado.
Los datos se ven como sigue:
library(tidyr)
dat_res <- dat_ing_f %>%
group_by(sexojefe, nivelaprob, decil, vehiculo) %>%
dplyr::summarise(num = n()) %>%
group_by(sexojefe, nivelaprob, decil) %>%
mutate(total = sum(num)) %>%
ungroup() %>%
mutate(prop = num/total)
dat_res
#> # A tibble: 228 x 7
#> sexojefe nivelaprob decil vehiculo num total prop
#> <fct> <fct> <fct> <fct> <int> <int> <dbl>
#> 1 1 No esp [10.08,10.28) TRUE 1 29352 0.0000341
#> 2 1 No esp [10.51,10.76) TRUE 1 29352 0.0000341
#> 3 1 No esp [11.14,14.35] TRUE 2 29352 0.0000681
#> 4 1 Ninguna/Pre [ 0.00, 9.05) FALSE 494 29352 0.0168
#> 5 1 Ninguna/Pre [ 0.00, 9.05) TRUE 2 29352 0.0000681
#> 6 1 Ninguna/Pre [ 9.05, 9.40) FALSE 352 29352 0.0120
#> 7 1 Ninguna/Pre [ 9.05, 9.40) TRUE 12 29352 0.000409
#> 8 1 Ninguna/Pre [ 9.40, 9.66) FALSE 239 29352 0.00814
#> 9 1 Ninguna/Pre [ 9.40, 9.66) TRUE 11 29352 0.000375
#> 10 1 Ninguna/Pre [ 9.66, 9.88) FALSE 187 29352 0.00637
#> # … with 218 more rows
dat_res_sub <- filter(dat_res, vehiculo==TRUE, num > 5)
cuadrado <- function(x){x ^ 2}
ggplot(dat_res_sub, aes(x = nivelaprob, y = prop, colour = decil,
group = decil)) +
geom_point(aes(size = sqrt(num))) +
geom_line() +
facet_wrap(~sexojefe) +
scale_size_continuous("# obs.", labels = cuadrado) +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) 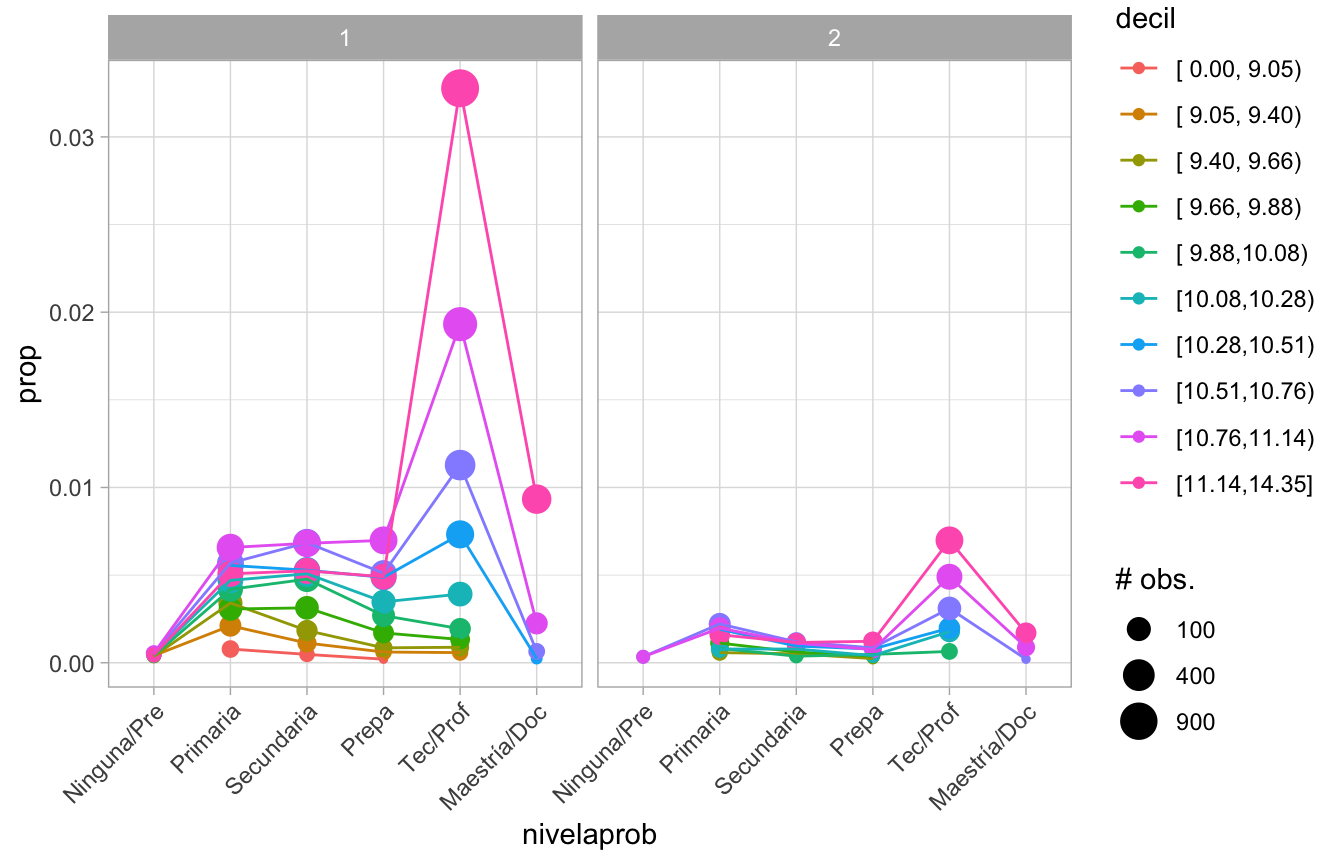
Comenzamos con un modelo simple, con poca regularización:
library(arm)
# vemos como se ve la variable vehículo
table(dat_ing$vehiculo)
#>
#> FALSE TRUE
#> 21813 7539
dat_ing$vehiculo_l <- as.logical(dat_ing$vehiculo == "TRUE")
table(dat_ing$vehiculo_l)
#>
#> FALSE TRUE
#> 21813 7539
# modelo con poca regularización
mod_1 <- bayesglm(vehiculo_l ~ sexojefe + nivelaprob + decil, data = dat_ing,
prior.scale = 2.5, family = 'binomial')
display(mod_1)
#> bayesglm(formula = vehiculo_l ~ sexojefe + nivelaprob + decil,
#> family = "binomial", data = dat_ing, prior.scale = 2.5)
#> coef.est coef.se
#> (Intercept) -2.23 0.68
#> sexojefe2 -0.42 0.04
#> nivelaprobNinguna/Pre -2.29 0.67
#> nivelaprobPrimaria -1.52 0.66
#> nivelaprobSecundaria -1.13 0.66
#> nivelaprobPrepa -0.72 0.66
#> nivelaprobTec/Prof -0.32 0.66
#> nivelaprobMaestría/Doc 0.26 0.67
#> decil[ 9.05, 9.40) 0.83 0.15
#> decil[ 9.40, 9.66) 1.29 0.14
#> decil[ 9.66, 9.88) 1.54 0.14
#> decil[ 9.88,10.08) 1.87 0.14
#> decil[10.08,10.28) 2.16 0.13
#> decil[10.28,10.51) 2.50 0.13
#> decil[10.51,10.76) 2.83 0.13
#> decil[10.76,11.14) 3.27 0.13
#> decil[11.14,14.35] 3.77 0.13
#> ---
#> n = 29352, k = 17
#> residual deviance = 25156.3, null deviance = 33445.7 (difference = 8289.4)
mod_1$aic
#> [1] 25190.31Agregamos las interacciones de sexojefe con decil.
mod_2 <- bayesglm(vehiculo ~ sexojefe + nivelaprob + decil +
sexojefe:decil, data = dat_ing, prior.scale = 2.5, family = 'binomial')
display(mod_2)
#> bayesglm(formula = vehiculo ~ sexojefe + nivelaprob + decil +
#> sexojefe:decil, family = "binomial", data = dat_ing, prior.scale = 2.5)
#> coef.est coef.se
#> (Intercept) -2.20 0.68
#> sexojefe2 -0.56 0.29
#> nivelaprobNinguna/Pre -2.29 0.67
#> nivelaprobPrimaria -1.53 0.66
#> nivelaprobSecundaria -1.14 0.66
#> nivelaprobPrepa -0.72 0.66
#> nivelaprobTec/Prof -0.33 0.66
#> nivelaprobMaestría/Doc 0.26 0.67
#> decil[ 9.05, 9.40) 0.92 0.16
#> decil[ 9.40, 9.66) 1.30 0.15
#> decil[ 9.66, 9.88) 1.48 0.15
#> decil[ 9.88,10.08) 1.87 0.15
#> decil[10.08,10.28) 2.18 0.14
#> decil[10.28,10.51) 2.46 0.14
#> decil[10.51,10.76) 2.78 0.14
#> decil[10.76,11.14) 3.23 0.14
#> decil[11.14,14.35] 3.70 0.14
#> sexojefe2:decil[ 9.05, 9.40) -0.69 0.40
#> sexojefe2:decil[ 9.40, 9.66) -0.06 0.34
#> sexojefe2:decil[ 9.66, 9.88) 0.28 0.32
#> sexojefe2:decil[ 9.88,10.08) -0.05 0.32
#> sexojefe2:decil[10.08,10.28) -0.05 0.31
#> sexojefe2:decil[10.28,10.51) 0.23 0.31
#> sexojefe2:decil[10.51,10.76) 0.23 0.31
#> sexojefe2:decil[10.76,11.14) 0.20 0.31
#> sexojefe2:decil[11.14,14.35] 0.36 0.31
#> ---
#> n = 29352, k = 26
#> residual deviance = 25131.3, null deviance = 33445.7 (difference = 8314.3)
mod_2$aic
#> [1] 25183.34Agregamos ahora la interacción sexojefe con nivelaprob, notemos que incluir esta interacción incrementa considerablemente el aic,
mod_3 <- bayesglm(vehiculo ~ sexojefe + nivelaprob + decil +
sexojefe:nivelaprob + decil:nivelaprob, data = dat_ing,
prior.scale = 2.5, family = 'binomial')
display(mod_3)
#> bayesglm(formula = vehiculo ~ sexojefe + nivelaprob + decil +
#> sexojefe:nivelaprob + decil:nivelaprob, family = "binomial",
#> data = dat_ing, prior.scale = 2.5)
#> coef.est coef.se
#> (Intercept) -1.83 0.74
#> sexojefe2 -0.35 0.70
#> nivelaprobNinguna/Pre -3.32 0.81
#> nivelaprobPrimaria -2.14 0.75
#> nivelaprobSecundaria -1.21 0.75
#> nivelaprobPrepa -0.60 0.77
#> nivelaprobTec/Prof -0.40 0.78
#> nivelaprobMaestría/Doc 0.86 0.94
#> decil[ 9.05, 9.40) 0.86 0.77
#> decil[ 9.40, 9.66) 0.97 0.79
#> decil[ 9.66, 9.88) 1.05 0.75
#> decil[ 9.88,10.08) 1.73 0.78
#> decil[10.08,10.28) 1.99 0.72
#> decil[10.28,10.51) 1.93 0.76
#> decil[10.51,10.76) 2.55 0.73
#> decil[10.76,11.14) 2.89 0.77
#> decil[11.14,14.35] 3.50 0.73
#> sexojefe2:nivelaprobNinguna/Pre 0.08 0.72
#> sexojefe2:nivelaprobPrimaria 0.05 0.70
#> sexojefe2:nivelaprobSecundaria -0.13 0.70
#> sexojefe2:nivelaprobPrepa 0.14 0.70
#> sexojefe2:nivelaprobTec/Prof -0.20 0.70
#> sexojefe2:nivelaprobMaestría/Doc -0.28 0.73
#> nivelaprobNinguna/Pre:decil[ 9.05, 9.40) 0.71 0.86
#> nivelaprobPrimaria:decil[ 9.05, 9.40) 0.05 0.79
#> nivelaprobSecundaria:decil[ 9.05, 9.40) -0.41 0.80
#> nivelaprobPrepa:decil[ 9.05, 9.40) -0.36 0.83
#> nivelaprobTec/Prof:decil[ 9.05, 9.40) 0.01 0.85
#> nivelaprobMaestría/Doc:decil[ 9.05, 9.40) 1.29 1.74
#> nivelaprobNinguna/Pre:decil[ 9.40, 9.66) 0.87 0.89
#> nivelaprobPrimaria:decil[ 9.40, 9.66) 0.60 0.81
#> nivelaprobSecundaria:decil[ 9.40, 9.66) 0.02 0.82
#> nivelaprobPrepa:decil[ 9.40, 9.66) -0.35 0.85
#> nivelaprobTec/Prof:decil[ 9.40, 9.66) -0.17 0.86
#> nivelaprobMaestría/Doc:decil[ 9.40, 9.66) 0.00 2.50
#> nivelaprobNinguna/Pre:decil[ 9.66, 9.88) 0.45 0.87
#> nivelaprobPrimaria:decil[ 9.66, 9.88) 0.72 0.77
#> nivelaprobSecundaria:decil[ 9.66, 9.88) 0.33 0.78
#> nivelaprobPrepa:decil[ 9.66, 9.88) -0.06 0.80
#> nivelaprobTec/Prof:decil[ 9.66, 9.88) -0.10 0.82
#> nivelaprobMaestría/Doc:decil[ 9.66, 9.88) -0.42 1.27
#> nivelaprobNinguna/Pre:decil[ 9.88,10.08) 0.77 0.87
#> nivelaprobPrimaria:decil[ 9.88,10.08) 0.34 0.79
#> nivelaprobSecundaria:decil[ 9.88,10.08) -0.13 0.80
#> nivelaprobPrepa:decil[ 9.88,10.08) -0.32 0.82
#> nivelaprobTec/Prof:decil[ 9.88,10.08) -0.41 0.84
#> nivelaprobMaestría/Doc:decil[ 9.88,10.08) 1.77 1.64
#> nivelaprobNinguna/Pre:decil[10.08,10.28) 0.88 0.81
#> nivelaprobPrimaria:decil[10.08,10.28) 0.31 0.74
#> nivelaprobSecundaria:decil[10.08,10.28) -0.15 0.74
#> nivelaprobPrepa:decil[10.08,10.28) -0.36 0.77
#> nivelaprobTec/Prof:decil[10.08,10.28) -0.05 0.78
#> nivelaprobMaestría/Doc:decil[10.08,10.28) -1.03 1.03
#> nivelaprobNinguna/Pre:decil[10.28,10.51) 0.69 0.86
#> nivelaprobPrimaria:decil[10.28,10.51) 0.77 0.78
#> nivelaprobSecundaria:decil[10.28,10.51) 0.18 0.78
#> nivelaprobPrepa:decil[10.28,10.51) 0.17 0.80
#> nivelaprobTec/Prof:decil[10.28,10.51) 0.31 0.82
#> nivelaprobMaestría/Doc:decil[10.28,10.51) -0.88 1.03
#> nivelaprobNinguna/Pre:decil[10.51,10.76) 0.99 0.81
#> nivelaprobPrimaria:decil[10.51,10.76) 0.45 0.74
#> nivelaprobSecundaria:decil[10.51,10.76) 0.04 0.75
#> nivelaprobPrepa:decil[10.51,10.76) -0.31 0.77
#> nivelaprobTec/Prof:decil[10.51,10.76) -0.04 0.78
#> nivelaprobMaestría/Doc:decil[10.51,10.76) -0.94 0.98
#> nivelaprobNinguna/Pre:decil[10.76,11.14) 1.29 0.86
#> nivelaprobPrimaria:decil[10.76,11.14) 0.63 0.79
#> nivelaprobSecundaria:decil[10.76,11.14) -0.02 0.79
#> nivelaprobPrepa:decil[10.76,11.14) -0.20 0.81
#> nivelaprobTec/Prof:decil[10.76,11.14) 0.09 0.82
#> nivelaprobMaestría/Doc:decil[10.76,11.14) -0.19 1.00
#> nivelaprobNinguna/Pre:decil[11.14,14.35] 1.05 0.83
#> nivelaprobPrimaria:decil[11.14,14.35] 0.53 0.75
#> nivelaprobSecundaria:decil[11.14,14.35] -0.16 0.76
#> nivelaprobPrepa:decil[11.14,14.35] -0.51 0.78
#> nivelaprobTec/Prof:decil[11.14,14.35] 0.05 0.79
#> nivelaprobMaestría/Doc:decil[11.14,14.35] -0.71 0.96
#> ---
#> n = 29352, k = 77
#> residual deviance = 25081.4, null deviance = 33445.7 (difference = 8364.2)
mod_3$aic
#> [1] 25235.44Ahora vemos las probabilidades estimadas del modelo 2:
# creamos una base con todas las combinaciones de niveles de las variables
grid_1 <- expand.grid(list(sexojefe = unique(dat_ing$sexojefe),
nivelaprob = unique(dat_ing$nivelaprob),
decil = unique(dat_ing$decil)), stringsAsFactors = FALSE)
# calculamos la probabilidad para cada caso usando predict
grid_1$prob <- predict(mod_2, grid_1, type = 'response')
grid_1$metodo <- "logística"
# obtenemos la siguietnte base de datos
head(grid_1)
#> sexojefe nivelaprob decil prob metodo
#> 1 1 Prepa [ 0.00, 9.05) 0.05125458 logística
#> 2 2 Prepa [ 0.00, 9.05) 0.02985596 logística
#> 3 1 Primaria [ 0.00, 9.05) 0.02362099 logística
#> 4 2 Primaria [ 0.00, 9.05) 0.01359400 logística
#> 5 1 Maestría/Doc [ 0.00, 9.05) 0.12607151 logística
#> 6 2 Maestría/Doc [ 0.00, 9.05) 0.07593718 logística
# y unimos con proporciones (MLE) para comparar
dat_res$metodo <- "proporción"
probs_est <- filter(dat_res, vehiculo == TRUE) %>%
dplyr::select(sexojefe, nivelaprob, decil, prob = prop, metodo) %>%
rbind(grid_1) %>%
filter(nivelaprob != "No esp")
ggplot(probs_est, aes(x = nivelaprob, y = prob, colour = decil, group = decil)) +
geom_line() +
facet_grid(metodo ~ sexojefe) +
theme(axis.text.x=element_text(angle = 45, hjust = 1))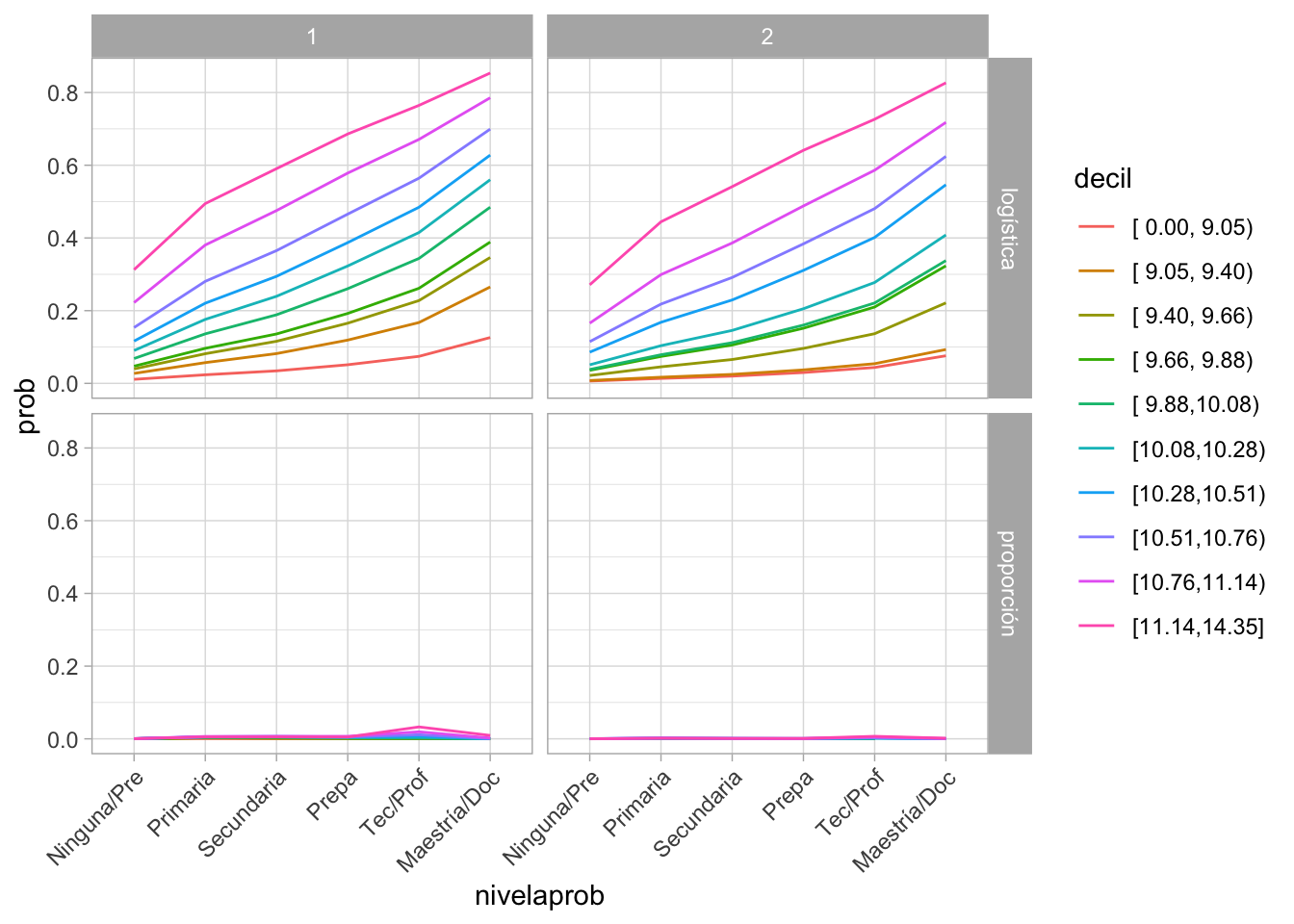
Y podemos incluir intervalos de probabilidad.
# realizamos simulaciones de los parámetros
sims <- sim(mod_2, 100)
str(sims)
#> Formal class 'sim' [package "arm"] with 2 slots
#> ..@ coef : num [1:100, 1:26] -3.08 -3.55 -1.66 -1.93 -2.9 ...
#> .. ..- attr(*, "dimnames")=List of 2
#> .. .. ..$ : NULL
#> .. .. ..$ : chr [1:26] "(Intercept)" "sexojefe2" "nivelaprobNinguna/Pre" "nivelaprobPrimaria" ...
#> ..@ sigma: num [1:100] 1 1 1 1 1 1 1 1 1 1 ...
# y los utilizamos en la función predict
mod_2$coefficients <- sims@coef[3, ]
grid_1$prob <- predict(mod_2, grid_1, type='response')
# repetimos este procedimiento para cada conjunto de coeficientes simulados
dat_sims <- ldply(1:100, function(i){
mod_2$coefficients <- sims@coef[i, ]
grid_1$prob <- predict(mod_2, grid_1, type='response')
grid_1$sim_no <- i
grid_1
})
# calculamos los cuantiles a partir de las probabilidades simuladas
dat_sims_1 <- dat_sims %>%
group_by(sexojefe, nivelaprob, decil) %>%
dplyr::summarise(
media = mean(prob),
q_10 = quantile(prob, 0.1),
q_90 = quantile(prob,0.9)
) %>%
ungroup() %>%
filter(nivelaprob != 'No esp')
ggplot(dat_sims_1, aes(x = nivelaprob, y = media, colour = decil, group = decil,
ymin = q_10, ymax = q_90)) +
geom_point() +
geom_line() +
facet_wrap(~ sexojefe) +
geom_linerange() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))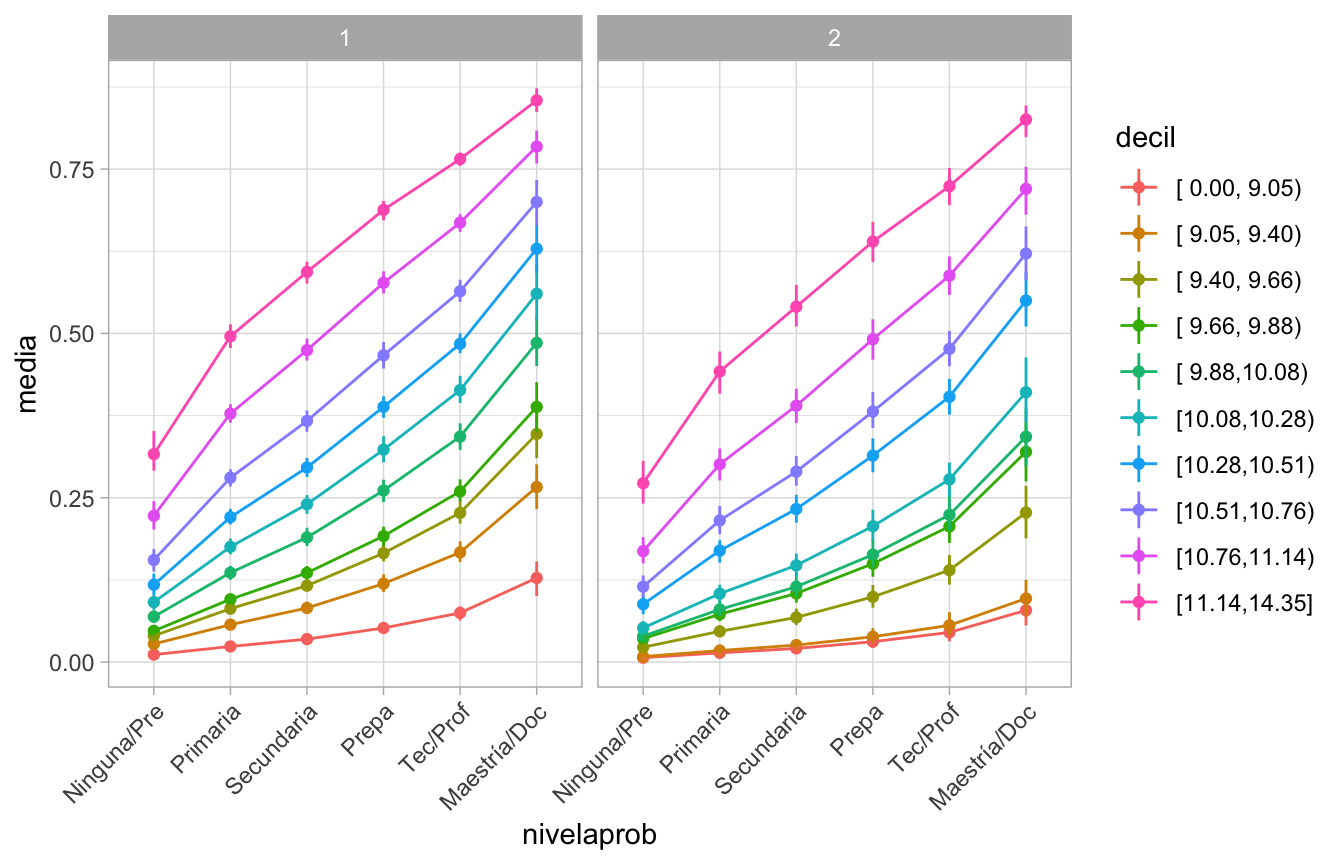
Finalmente checamos la calibración del modelo con los datos (las probabilidades estimadas reflejan probabilidades empíricas:
library(Hmisc) # función cut2
#> Loading required package: lattice
#> Loading required package: survival
#> Loading required package: Formula
#>
#> Attaching package: 'Hmisc'
#> The following objects are masked from 'package:plyr':
#>
#> is.discrete, summarize
#> The following object is masked from 'package:bnlearn':
#>
#> impute
#> The following objects are masked from 'package:dplyr':
#>
#> src, summarize
#> The following objects are masked from 'package:base':
#>
#> format.pval, units
mod_2 <- bayesglm(vehiculo ~ sexojefe + nivelaprob + decil +
sexojefe:decil, data = dat_ing, prior.scale = 2.5, family = 'binomial')
# predecimos para las observaciones en la base de datos
dat_ing$prob <- predict(mod_2, type = 'response')
dat_cal <- dat_ing_f %>%
mutate(
prob = predict(mod_2, type = 'response'),
grupo_prob = cut2(prob, g = 20, levels.mean = TRUE)
) %>%
group_by(grupo_prob) %>%
dplyr::summarise(
num = n(),
total_vehiculo = sum(vehiculo == TRUE)
) %>%
mutate(
prob_emp = total_vehiculo / num,
grupo_prob_n = as.numeric(as.character(grupo_prob))
)
ggplot(dat_cal, aes(x = grupo_prob_n, y = prob_emp)) +
geom_abline(intercept = 0, slope = 1, color = "red") +
geom_point() +
xlab("Probabilidades empíricas") +
ylab("Probabilidades estimadas")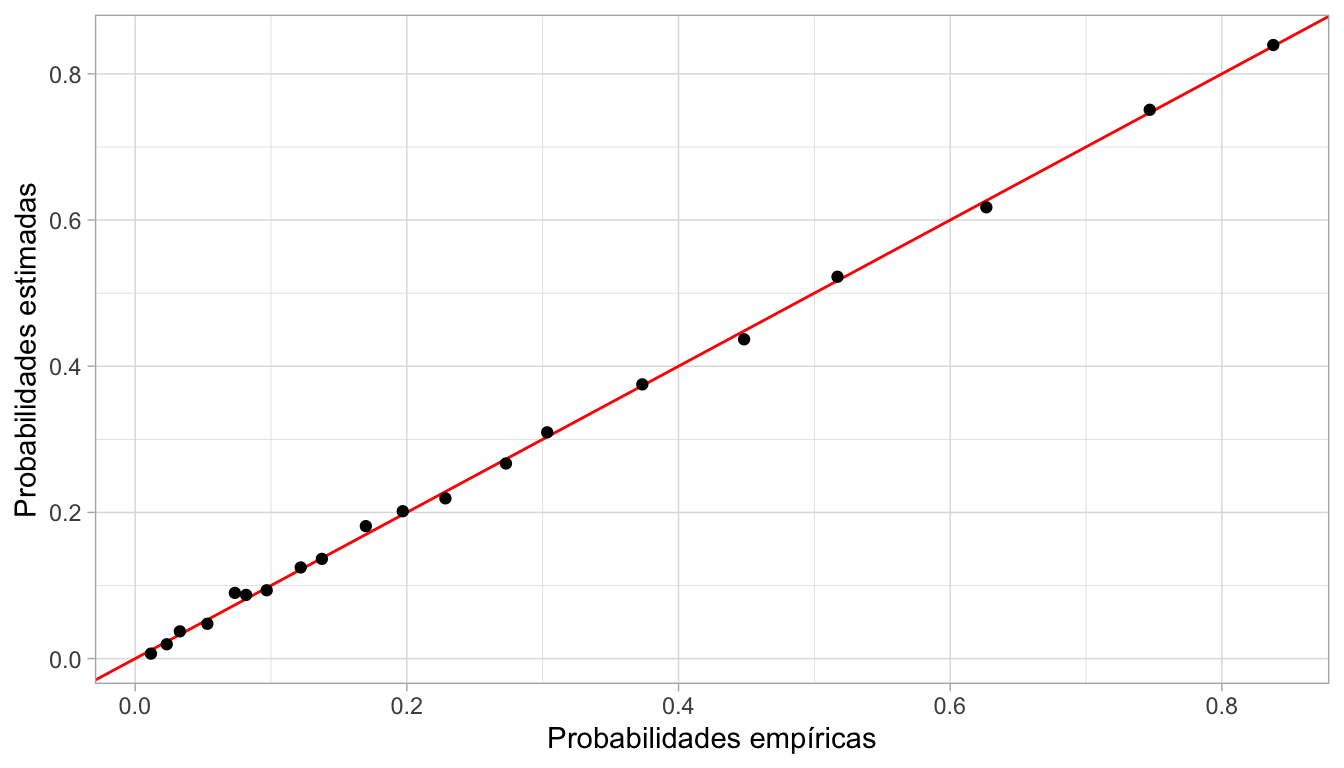
Y obtenemos la tabla de la probabilidad condicional,
grid_1
#> sexojefe nivelaprob decil prob metodo
#> 1 1 Prepa [ 0.00, 9.05) 0.055222904 logística
#> 2 2 Prepa [ 0.00, 9.05) 0.021890579 logística
#> 3 1 Primaria [ 0.00, 9.05) 0.025523017 logística
#> 4 2 Primaria [ 0.00, 9.05) 0.009929027 logística
#> 5 1 Maestría/Doc [ 0.00, 9.05) 0.140937236 logística
#> 6 2 Maestría/Doc [ 0.00, 9.05) 0.059104709 logística
#> 7 1 Ninguna/Pre [ 0.00, 9.05) 0.012764217 logística
#> 8 2 Ninguna/Pre [ 0.00, 9.05) 0.004926160 logística
#> 9 1 Secundaria [ 0.00, 9.05) 0.036038532 logística
#> 10 2 Secundaria [ 0.00, 9.05) 0.014112844 logística
#> 11 1 Tec/Prof [ 0.00, 9.05) 0.078857904 logística
#> 12 2 Tec/Prof [ 0.00, 9.05) 0.031738839 logística
#> 13 1 No esp [ 0.00, 9.05) 0.159233124 logística
#> 14 2 No esp [ 0.00, 9.05) 0.067613545 logística
#> 15 1 Prepa [ 9.05, 9.40) 0.136702875 logística
#> 16 2 Prepa [ 9.05, 9.40) 0.040116179 logística
#> 17 1 Primaria [ 9.05, 9.40) 0.066254649 logística
#> 18 2 Primaria [ 9.05, 9.40) 0.018382881 logística
#> 19 1 Maestría/Doc [ 9.05, 9.40) 0.307697627 logística
#> 20 2 Maestría/Doc [ 9.05, 9.40) 0.104988229 logística
#> 21 1 Ninguna/Pre [ 9.05, 9.40) 0.033841466 logística
#> 22 2 Ninguna/Pre [ 9.05, 9.40) 0.009159840 logística
#> 23 1 Secundaria [ 9.05, 9.40) 0.091967865 logística
#> 24 2 Secundaria [ 9.05, 9.40) 0.026035245 logística
#> 25 1 Tec/Prof [ 9.05, 9.40) 0.188261746 logística
#> 26 2 Tec/Prof [ 9.05, 9.40) 0.057680346 logística
#> 27 1 No esp [ 9.05, 9.40) 0.339096520 logística
#> 28 2 No esp [ 9.05, 9.40) 0.119265260 logística
#> 29 1 Prepa [ 9.40, 9.66) 0.152958317 logística
#> 30 2 Prepa [ 9.40, 9.66) 0.116679658 logística
#> 31 1 Primaria [ 9.40, 9.66) 0.074859442 logística
#> 32 2 Primaria [ 9.40, 9.66) 0.055882219 logística
#> 33 1 Maestría/Doc [ 9.40, 9.66) 0.336363853 logística
#> 34 2 Maestría/Doc [ 9.40, 9.66) 0.270475427 logística
#> 35 1 Ninguna/Pre [ 9.40, 9.66) 0.038409776 logística
#> 36 2 Ninguna/Pre [ 9.40, 9.66) 0.028389169 logística
#> 37 1 Secundaria [ 9.40, 9.66) 0.103541838 logística
#> 38 2 Secundaria [ 9.40, 9.66) 0.077905791 logística
#> 39 1 Tec/Prof [ 9.40, 9.66) 0.209162675 logística
#> 40 2 Tec/Prof [ 9.40, 9.66) 0.162104631 logística
#> 41 1 No esp [ 9.40, 9.66) 0.369128276 logística
#> 42 2 No esp [ 9.40, 9.66) 0.299720413 logística
#> 43 1 Prepa [ 9.66, 9.88) 0.178986431 logística
#> 44 2 Prepa [ 9.66, 9.88) 0.145018515 logística
#> 45 1 Primaria [ 9.66, 9.88) 0.088994156 logística
#> 46 2 Primaria [ 9.66, 9.88) 0.070635553 logística
#> 47 1 Maestría/Doc [ 9.66, 9.88) 0.379614278 logística
#> 48 2 Maestría/Doc [ 9.66, 9.88) 0.322528827 logística
#> 49 1 Ninguna/Pre [ 9.66, 9.88) 0.046004419 logística
#> 50 2 Ninguna/Pre [ 9.66, 9.88) 0.036162142 logística
#> 51 1 Secundaria [ 9.66, 9.88) 0.122375886 logística
#> 52 2 Secundaria [ 9.66, 9.88) 0.097870775 logística
#> 53 1 Tec/Prof [ 9.66, 9.88) 0.242022103 logística
#> 54 2 Tec/Prof [ 9.66, 9.88) 0.198990787 logística
#> 55 1 No esp [ 9.66, 9.88) 0.413963683 logística
#> 56 2 No esp [ 9.66, 9.88) 0.354665828 logística
#> 57 1 Prepa [ 9.88,10.08) 0.263771401 logística
#> 58 2 Prepa [ 9.88,10.08) 0.151229920 logística
#> 59 1 Primaria [ 9.88,10.08) 0.138332791 logística
#> 60 2 Primaria [ 9.88,10.08) 0.073936514 logística
#> 61 1 Maestría/Doc [ 9.88,10.08) 0.501396511 logística
#> 62 2 Maestría/Doc [ 9.88,10.08) 0.333378685 logística
#> 63 1 Ninguna/Pre [ 9.88,10.08) 0.073430493 logística
#> 64 2 Ninguna/Pre [ 9.88,10.08) 0.037917811 logística
#> 65 1 Secundaria [ 9.88,10.08) 0.186434079 logística
#> 66 2 Secundaria [ 9.88,10.08) 0.102304395 logística
#> 67 1 Tec/Prof [ 9.88,10.08) 0.344150252 logística
#> 68 2 Tec/Prof [ 9.88,10.08) 0.206954351 logística
#> 69 1 No esp [ 9.88,10.08) 0.537223074 logística
#> 70 2 No esp [ 9.88,10.08) 0.366012702 logística
#> 71 1 Prepa [10.08,10.28) 0.322760377 logística
#> 72 2 Prepa [10.08,10.28) 0.197418922 logística
#> 73 1 Primaria [10.08,10.28) 0.175974272 logística
#> 74 2 Primaria [10.08,10.28) 0.099279680 logística
#> 75 1 Maestría/Doc [10.08,10.28) 0.572223534 logística
#> 76 2 Maestría/Doc [10.08,10.28) 0.408429632 logística
#> 77 1 Ninguna/Pre [10.08,10.28) 0.095366121 logística
#> 78 2 Ninguna/Pre [10.08,10.28) 0.051602831 logística
#> 79 1 Secundaria [10.08,10.28) 0.233615683 logística
#> 80 2 Secundaria [10.08,10.28) 0.135943793 logística
#> 81 1 Tec/Prof [10.08,10.28) 0.411078063 logística
#> 82 2 Tec/Prof [10.08,10.28) 0.264852044 logística
#> 83 1 No esp [10.08,10.28) 0.606950373 logística
#> 84 2 No esp [10.08,10.28) 0.443522358 logística
#> 85 1 Prepa [10.28,10.51) 0.389895264 logística
#> 86 2 Prepa [10.28,10.51) 0.274124768 logística
#> 87 1 Primaria [10.28,10.51) 0.222613345 logística
#> 88 2 Primaria [10.28,10.51) 0.144730435 logística
#> 89 1 Maestría/Doc [10.28,10.51) 0.642054261 logística
#> 90 2 Maestría/Doc [10.28,10.51) 0.514558163 logística
#> 91 1 Ninguna/Pre [10.28,10.51) 0.123852357 logística
#> 92 2 Ninguna/Pre [10.28,10.51) 0.077095082 logística
#> 93 1 Secundaria [10.28,10.51) 0.290152421 logística
#> 94 2 Secundaria [10.28,10.51) 0.194554034 logística
#> 95 1 Tec/Prof [10.28,10.51) 0.483469021 logística
#> 96 2 Tec/Prof [10.28,10.51) 0.356132452 logística
#> 97 1 No esp [10.28,10.51) 0.674338483 logística
#> 98 2 No esp [10.28,10.51) 0.550287243 logística
#> 99 1 Prepa [10.51,10.76) 0.465701152 logística
#> 100 2 Prepa [10.51,10.76) 0.384348226 logística
#> 101 1 Primaria [10.51,10.76) 0.280867990 logística
#> 102 2 Primaria [10.51,10.76) 0.218593528 logística
#> 103 1 Maestría/Doc [10.51,10.76) 0.709845274 logística
#> 104 2 Maestría/Doc [10.51,10.76) 0.636663390 logística
#> 105 1 Ninguna/Pre [10.51,10.76) 0.161636318 logística
#> 106 2 Ninguna/Pre [10.51,10.76) 0.121337552 logística
#> 107 1 Secundaria [10.51,10.76) 0.357943167 logística
#> 108 2 Secundaria [10.51,10.76) 0.285360705 logística
#> 109 1 Tec/Prof [10.51,10.76) 0.560746755 logística
#> 110 2 Tec/Prof [10.51,10.76) 0.477632925 logística
#> 111 1 No esp [10.51,10.76) 0.738505428 logística
#> 112 2 No esp [10.51,10.76) 0.669183308 logística
#> 113 1 Prepa [10.76,11.14) 0.576384346 logística
#> 114 2 Prepa [10.76,11.14) 0.507590226 logística
#> 115 1 Primaria [10.76,11.14) 0.378763268 logística
#> 116 2 Primaria [10.76,11.14) 0.315963250 logística
#> 117 1 Maestría/Doc [10.76,11.14) 0.792488633 logística
#> 118 2 Maestría/Doc [10.76,11.14) 0.743150284 logística
#> 119 1 Ninguna/Pre [10.76,11.14) 0.231342925 logística
#> 120 2 Ninguna/Pre [10.76,11.14) 0.185679992 logística
#> 121 1 Secundaria [10.76,11.14) 0.465319958 logística
#> 122 2 Secundaria [10.76,11.14) 0.397347828 logística
#> 123 1 Tec/Prof [10.76,11.14) 0.665867394 logística
#> 124 2 Tec/Prof [10.76,11.14) 0.601559604 logística
#> 125 1 No esp [10.76,11.14) 0.815111845 logística
#> 126 2 No esp [10.76,11.14) 0.769588544 logística
#> 127 1 Prepa [11.14,14.35] 0.683303088 logística
#> 128 2 Prepa [11.14,14.35] 0.625774335 logística
#> 129 1 Primaria [11.14,14.35] 0.491561887 logística
#> 130 2 Primaria [11.14,14.35] 0.428342200 logística
#> 131 1 Maestría/Doc [11.14,14.35] 0.858275148 logística
#> 132 2 Maestría/Doc [11.14,14.35] 0.824360556 logística
#> 133 1 Ninguna/Pre [11.14,14.35] 0.323070051 logística
#> 134 2 Ninguna/Pre [11.14,14.35] 0.270012114 logística
#> 135 1 Secundaria [11.14,14.35] 0.579836419 logística
#> 136 2 Secundaria [11.14,14.35] 0.516803524 logística
#> 137 1 Tec/Prof [11.14,14.35] 0.759620088 logística
#> 138 2 Tec/Prof [11.14,14.35] 0.710072315 logística
#> 139 1 No esp [11.14,14.35] 0.874858761 logística
#> 140 2 No esp [11.14,14.35] 0.844192193 logísticaque incluimos a nuestro modelo local en la red:
fit_enigh <- bn.fit(net_enigh, data = dat_ing_f, method = 'mle')
fit_enigh[['vehiculo']]
#>
#> Parameters of node vehiculo (multinomial distribution)
#>
#> Conditional probability table:
#>
#> , , nivelaprob = No esp, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE
#> TRUE
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.000000000 0.000000000
#> TRUE 1.000000000 1.000000000
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.000000000
#> TRUE 1.000000000
#>
#> , , nivelaprob = Ninguna/Pre, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.995967742 0.967032967 0.956000000 0.979057592
#> TRUE 0.004032258 0.032967033 0.044000000 0.020942408
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.920529801 0.898550725 0.945054945 0.859813084
#> TRUE 0.079470199 0.101449275 0.054945055 0.140186916
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.728813559 0.675000000
#> TRUE 0.271186441 0.325000000
#>
#> , , nivelaprob = Primaria, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.981300813 0.948717949 0.908759124 0.906542056
#> TRUE 0.018699187 0.051282051 0.091240876 0.093457944
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.863181313 0.826415094 0.793670886 0.736176935
#> TRUE 0.136818687 0.173584906 0.206329114 0.263823065
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.630975143 0.487972509
#> TRUE 0.369024857 0.512027491
#>
#> , , nivelaprob = Secundaria, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.958823529 0.923255814 0.894531250 0.843803056
#> TRUE 0.041176471 0.076744186 0.105468750 0.156196944
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.795620438 0.767912773 0.718693285 0.609708738
#> TRUE 0.204379562 0.232087227 0.281306715 0.390291262
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.535962877 0.437956204
#> TRUE 0.464037123 0.562043796
#>
#> , , nivelaprob = Prepa, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.918918919 0.864661654 0.864864865 0.814126394
#> TRUE 0.081081081 0.135338346 0.135135135 0.185873606
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.743506494 0.674121406 0.571856287 0.554896142
#> TRUE 0.256493506 0.325878594 0.428143713 0.445103858
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.428969359 0.381974249
#> TRUE 0.571030641 0.618025751
#>
#> , , nivelaprob = Tec/Prof, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.891891892 0.767123288 0.775862069 0.753164557
#> TRUE 0.108108108 0.232876712 0.224137931 0.246835443
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.721951220 0.566037736 0.485645933 0.425347222
#> TRUE 0.278048780 0.433962264 0.514354067 0.574652778
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.318509615 0.223567393
#> TRUE 0.681490385 0.776432607
#>
#> , , nivelaprob = Maestría/Doc, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.000000000 0.000000000 0.500000000
#> TRUE 1.000000000 1.000000000 0.500000000
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.000000000 0.571428571 0.500000000 0.296296296
#> TRUE 1.000000000 0.428571429 0.500000000 0.703703704
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.185185185 0.135646688
#> TRUE 0.814814815 0.864353312
#>
#> , , nivelaprob = No esp, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE
#> TRUE
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE
#> TRUE
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE
#> TRUE
#>
#> , , nivelaprob = Ninguna/Pre, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 1.000000000 0.989528796 0.990740741 0.971698113
#> TRUE 0.000000000 0.010471204 0.009259259 0.028301887
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.967741935 0.941176471 0.905660377 0.807692308
#> TRUE 0.032258065 0.058823529 0.094339623 0.192307692
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.761904762 0.583333333
#> TRUE 0.238095238 0.416666667
#>
#> , , nivelaprob = Primaria, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.991304348 0.987012987 0.959232614 0.907303371
#> TRUE 0.008695652 0.012987013 0.040767386 0.092696629
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.917525773 0.918149466 0.789473684 0.752851711
#> TRUE 0.082474227 0.081850534 0.210526316 0.247148289
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.613333333 0.548076923
#> TRUE 0.386666667 0.451923077
#>
#> , , nivelaprob = Secundaria, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.955056180 0.977443609 0.895833333 0.879194631
#> TRUE 0.044943820 0.022556391 0.104166667 0.120805369
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.926174497 0.835714286 0.789473684 0.715447154
#> TRUE 0.073825503 0.164285714 0.210526316 0.284552846
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.682692308 0.492537313
#> TRUE 0.317307692 0.507462687
#>
#> , , nivelaprob = Prepa, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.913043478 0.937500000 0.865384615 0.813559322
#> TRUE 0.086956522 0.062500000 0.134615385 0.186440678
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.725490196 0.806451613 0.671428571 0.553571429
#> TRUE 0.274509804 0.193548387 0.328571429 0.446428571
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.551020408 0.345454545
#> TRUE 0.448979592 0.654545455
#>
#> , , nivelaprob = Tec/Prof, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.958333333 0.935483871 0.943396226 0.928571429
#> TRUE 0.041666667 0.064516129 0.056603774 0.071428571
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.786516854 0.699421965 0.652694611 0.570754717
#> TRUE 0.213483146 0.300578035 0.347305389 0.429245283
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.454545455 0.257246377
#> TRUE 0.545454545 0.742753623
#>
#> , , nivelaprob = Maestría/Doc, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 1.000000000
#> TRUE 0.000000000
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.625000000 0.625000000 0.600000000
#> TRUE 0.375000000 0.375000000 0.400000000
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.161290323 0.253731343
#> TRUE 0.838709677 0.746268657
grid_1$vehiculo <- 'TRUE'
grid_2 <- grid_1
grid_2$prob <- 1 - grid_2$prob
grid_2$vehiculo <- 'FALSE'
grid_3 <- rbind(grid_1, grid_2)
tab_veh <- xtabs(prob ~ vehiculo + decil + nivelaprob + decil + sexojefe,
data = grid_3)
tab_veh
#> , , nivelaprob = No esp, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.840766876 0.660903480 0.630871724 0.586036317
#> TRUE 0.159233124 0.339096520 0.369128276 0.413963683
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.462776926 0.393049627 0.325661517 0.261494572
#> TRUE 0.537223074 0.606950373 0.674338483 0.738505428
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.184888155 0.125141239
#> TRUE 0.815111845 0.874858761
#>
#> , , nivelaprob = Ninguna/Pre, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.987235783 0.966158534 0.961590224 0.953995581
#> TRUE 0.012764217 0.033841466 0.038409776 0.046004419
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.926569507 0.904633879 0.876147643 0.838363682
#> TRUE 0.073430493 0.095366121 0.123852357 0.161636318
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.768657075 0.676929949
#> TRUE 0.231342925 0.323070051
#>
#> , , nivelaprob = Primaria, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.974476983 0.933745351 0.925140558 0.911005844
#> TRUE 0.025523017 0.066254649 0.074859442 0.088994156
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.861667209 0.824025728 0.777386655 0.719132010
#> TRUE 0.138332791 0.175974272 0.222613345 0.280867990
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.621236732 0.508438113
#> TRUE 0.378763268 0.491561887
#>
#> , , nivelaprob = Secundaria, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.963961468 0.908032135 0.896458162 0.877624114
#> TRUE 0.036038532 0.091967865 0.103541838 0.122375886
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.813565921 0.766384317 0.709847579 0.642056833
#> TRUE 0.186434079 0.233615683 0.290152421 0.357943167
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.534680042 0.420163581
#> TRUE 0.465319958 0.579836419
#>
#> , , nivelaprob = Prepa, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.944777096 0.863297125 0.847041683 0.821013569
#> TRUE 0.055222904 0.136702875 0.152958317 0.178986431
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.736228599 0.677239623 0.610104736 0.534298848
#> TRUE 0.263771401 0.322760377 0.389895264 0.465701152
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.423615654 0.316696912
#> TRUE 0.576384346 0.683303088
#>
#> , , nivelaprob = Tec/Prof, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.921142096 0.811738254 0.790837325 0.757977897
#> TRUE 0.078857904 0.188261746 0.209162675 0.242022103
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.655849748 0.588921937 0.516530979 0.439253245
#> TRUE 0.344150252 0.411078063 0.483469021 0.560746755
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.334132606 0.240379912
#> TRUE 0.665867394 0.759620088
#>
#> , , nivelaprob = Maestría/Doc, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.859062764 0.692302373 0.663636147 0.620385722
#> TRUE 0.140937236 0.307697627 0.336363853 0.379614278
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.498603489 0.427776466 0.357945739 0.290154726
#> TRUE 0.501396511 0.572223534 0.642054261 0.709845274
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.207511367 0.141724852
#> TRUE 0.792488633 0.858275148
#>
#> , , nivelaprob = No esp, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.932386455 0.880734740 0.700279587 0.645334172
#> TRUE 0.067613545 0.119265260 0.299720413 0.354665828
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.633987298 0.556477642 0.449712757 0.330816692
#> TRUE 0.366012702 0.443522358 0.550287243 0.669183308
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.230411456 0.155807807
#> TRUE 0.769588544 0.844192193
#>
#> , , nivelaprob = Ninguna/Pre, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.995073840 0.990840160 0.971610831 0.963837858
#> TRUE 0.004926160 0.009159840 0.028389169 0.036162142
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.962082189 0.948397169 0.922904918 0.878662448
#> TRUE 0.037917811 0.051602831 0.077095082 0.121337552
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.814320008 0.729987886
#> TRUE 0.185679992 0.270012114
#>
#> , , nivelaprob = Primaria, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.990070973 0.981617119 0.944117781 0.929364447
#> TRUE 0.009929027 0.018382881 0.055882219 0.070635553
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.926063486 0.900720320 0.855269565 0.781406472
#> TRUE 0.073936514 0.099279680 0.144730435 0.218593528
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.684036750 0.571657800
#> TRUE 0.315963250 0.428342200
#>
#> , , nivelaprob = Secundaria, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.985887156 0.973964755 0.922094209 0.902129225
#> TRUE 0.014112844 0.026035245 0.077905791 0.097870775
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.897695605 0.864056207 0.805445966 0.714639295
#> TRUE 0.102304395 0.135943793 0.194554034 0.285360705
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.602652172 0.483196476
#> TRUE 0.397347828 0.516803524
#>
#> , , nivelaprob = Prepa, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.978109421 0.959883821 0.883320342 0.854981485
#> TRUE 0.021890579 0.040116179 0.116679658 0.145018515
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.848770080 0.802581078 0.725875232 0.615651774
#> TRUE 0.151229920 0.197418922 0.274124768 0.384348226
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.492409774 0.374225665
#> TRUE 0.507590226 0.625774335
#>
#> , , nivelaprob = Tec/Prof, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.968261161 0.942319654 0.837895369 0.801009213
#> TRUE 0.031738839 0.057680346 0.162104631 0.198990787
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.793045649 0.735147956 0.643867548 0.522367075
#> TRUE 0.206954351 0.264852044 0.356132452 0.477632925
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.398440396 0.289927685
#> TRUE 0.601559604 0.710072315
#>
#> , , nivelaprob = Maestría/Doc, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.940895291 0.895011771 0.729524573 0.677471173
#> TRUE 0.059104709 0.104988229 0.270475427 0.322528827
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.666621315 0.591570368 0.485441837 0.363336610
#> TRUE 0.333378685 0.408429632 0.514558163 0.636663390
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.256849716 0.175639444
#> TRUE 0.743150284 0.824360556
fit_enigh_b[['vehiculo']] <- tab_veh2.3.5 Nodos multinomiales
En el siguiente ejemplo veremos cómo hacer un modelo multinomial: modelamos decil dado marginación y nivelaprobado. Utilizaremos una combinación de regresión Ridge y Lasso con el fin de regularizar, para esto usamos el paquete glmnet.
library(glmnet)
#> Loading required package: foreach
#>
#> Attaching package: 'foreach'
#> The following objects are masked from 'package:purrr':
#>
#> accumulate, when
#> Loaded glmnet 2.0-18
mat_1 <- model.matrix(~ -1 + marg + nivelaprob + marg:nivelaprob,
data = dat_ing)
mod_decil <- cv.glmnet(y = dat_ing$decil, x = mat_1, alpha = 0.5,
family = 'multinomial')
plot(mod_decil)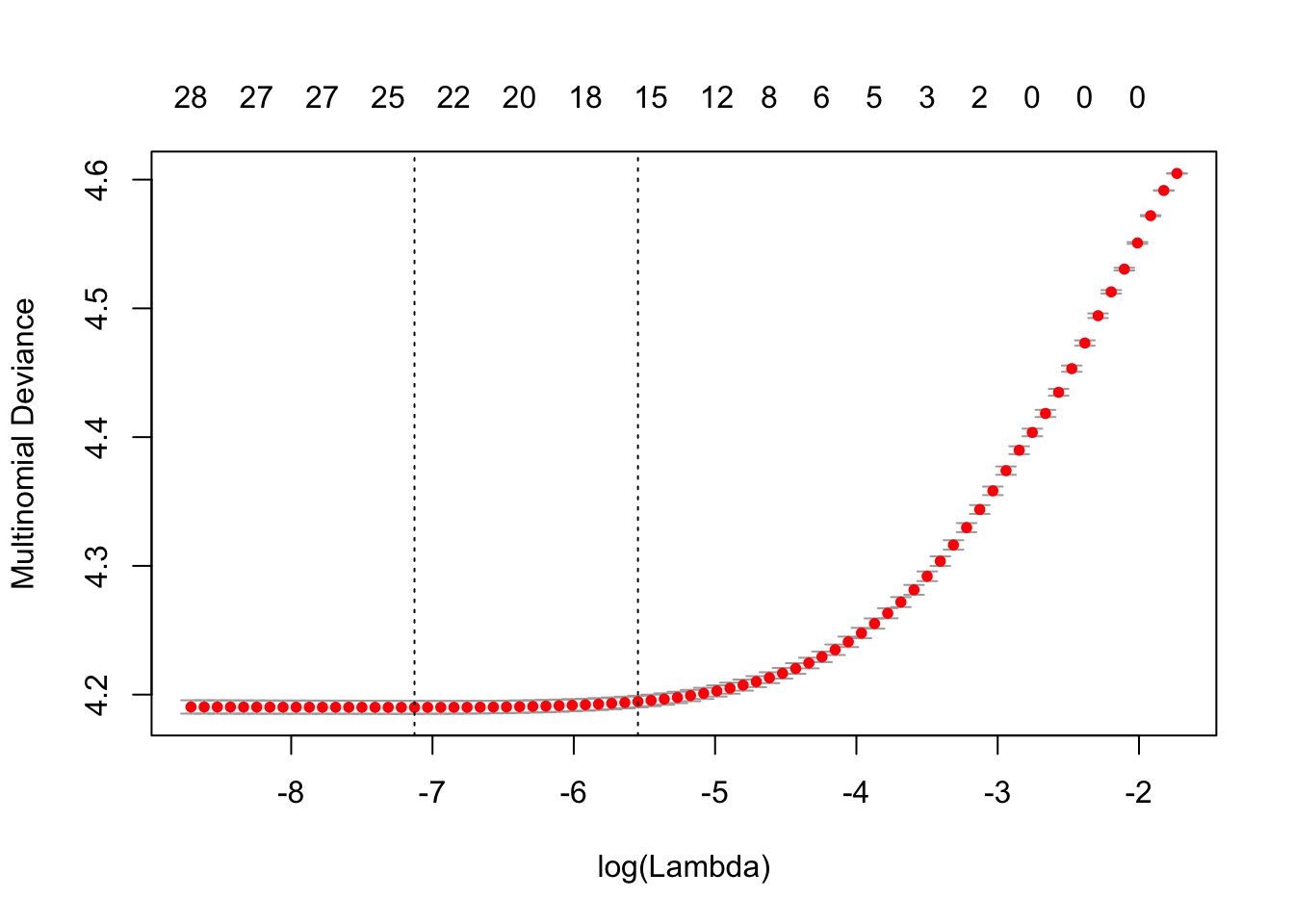
Hacemos las predicciones:
grid_pred <- expand.grid(list(marg = unique(dat_ing$marg),
nivelaprob = unique(dat_ing$nivelaprob)), stringsAsFactors = FALSE)
mat_pred <- model.matrix(~ -1 + marg + nivelaprob + marg:nivelaprob,
data = grid_pred)
mod_decil_pred <- predict(mod_decil, s = exp(-4), type = 'response',
newx = mat_pred)[, , 1]
dat_pred <- cbind(grid_pred, mod_decil_pred)
head(dat_pred)
#> marg nivelaprob [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66)
#> 1 Muy bajo Prepa 0.03914810 0.06244066 0.09399453
#> 2 Muy alto Prepa 0.25190497 0.15130553 0.09432400
#> 3 Medio Prepa 0.07455623 0.10606631 0.12864312
#> 4 Bajo Prepa 0.07138752 0.10642948 0.12908359
#> 5 Alto Prepa 0.13802519 0.14213274 0.11638987
#> 6 Muy bajo Primaria 0.05968775 0.08771010 0.11242190
#> [ 9.66, 9.88) [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> 1 0.11441952 0.12049940 0.11896727 0.12499420 0.11796459
#> 2 0.09301744 0.08426844 0.08262937 0.07389383 0.07047682
#> 3 0.12787015 0.11584299 0.11358977 0.10158112 0.09688378
#> 4 0.12830797 0.11623964 0.11397870 0.10192893 0.09721551
#> 5 0.11267780 0.10207960 0.10009409 0.08951219 0.08015747
#> 6 0.11271594 0.11870530 0.11719599 0.12313318 0.11349846
#> [10.76,11.14) [11.14,14.35]
#> 1 0.13268287 0.07488885
#> 2 0.05457609 0.04360351
#> 3 0.07502521 0.05994132
#> 4 0.07528210 0.06014656
#> 5 0.06611141 0.05281965
#> 6 0.09632129 0.05861008Y ahora podemos examinar cómo están las predicciones del modelo.
dat_pred_l <- gather(dat_pred, nivel_decil, prob, 3:12)
ggplot(dat_pred_l, aes(x = nivelaprob, y = prob, colour = marg, group = marg)) +
geom_point() +
geom_line() +
facet_wrap(~ nivel_decil, nrow = 2) +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) 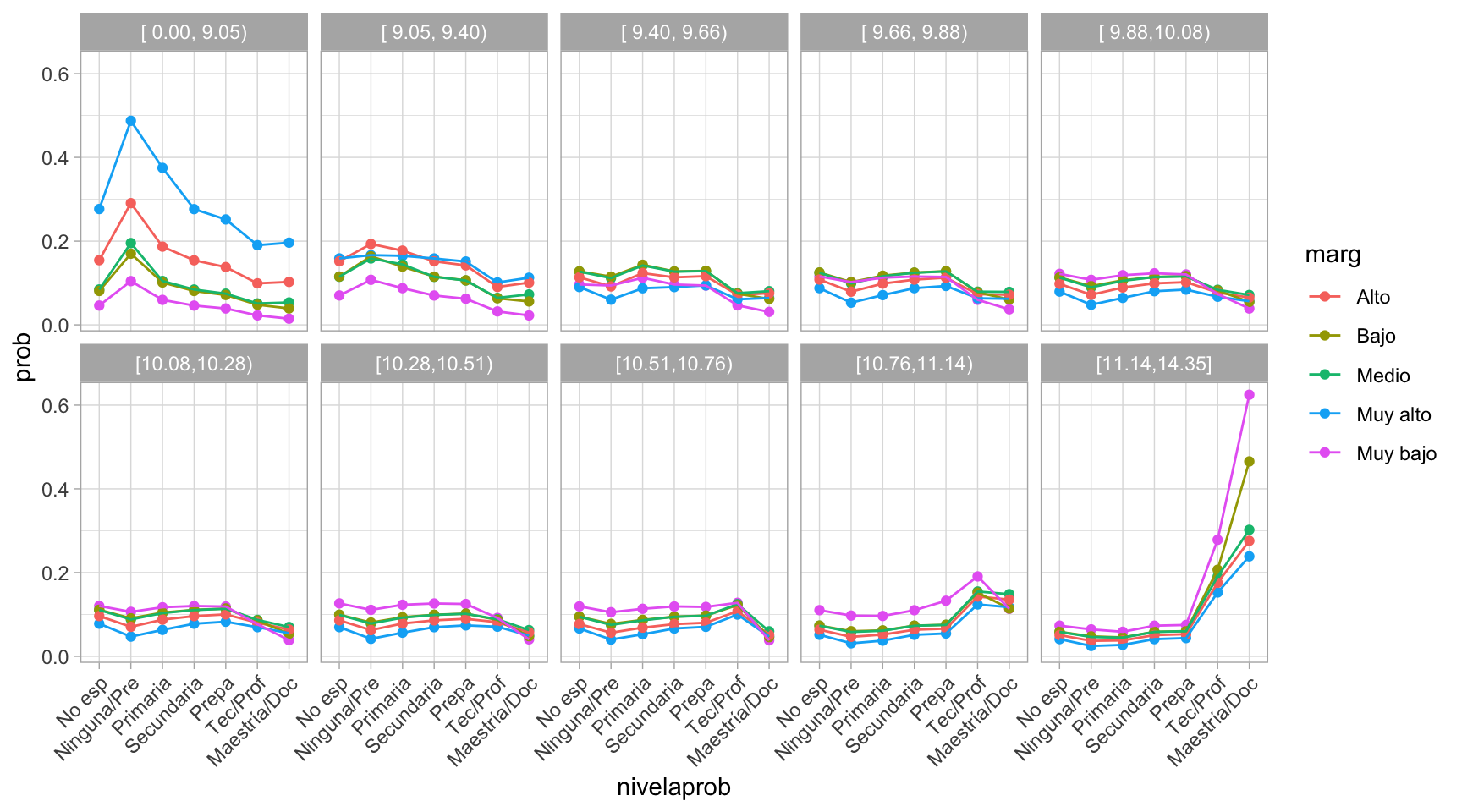
colnames(dat_pred_l)[3] <- "decil"
tab_decil <- xtabs(prob ~ decil + marg + nivelaprob, data = dat_pred_l)
tab_veh
#> , , nivelaprob = No esp, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.840766876 0.660903480 0.630871724 0.586036317
#> TRUE 0.159233124 0.339096520 0.369128276 0.413963683
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.462776926 0.393049627 0.325661517 0.261494572
#> TRUE 0.537223074 0.606950373 0.674338483 0.738505428
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.184888155 0.125141239
#> TRUE 0.815111845 0.874858761
#>
#> , , nivelaprob = Ninguna/Pre, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.987235783 0.966158534 0.961590224 0.953995581
#> TRUE 0.012764217 0.033841466 0.038409776 0.046004419
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.926569507 0.904633879 0.876147643 0.838363682
#> TRUE 0.073430493 0.095366121 0.123852357 0.161636318
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.768657075 0.676929949
#> TRUE 0.231342925 0.323070051
#>
#> , , nivelaprob = Primaria, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.974476983 0.933745351 0.925140558 0.911005844
#> TRUE 0.025523017 0.066254649 0.074859442 0.088994156
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.861667209 0.824025728 0.777386655 0.719132010
#> TRUE 0.138332791 0.175974272 0.222613345 0.280867990
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.621236732 0.508438113
#> TRUE 0.378763268 0.491561887
#>
#> , , nivelaprob = Secundaria, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.963961468 0.908032135 0.896458162 0.877624114
#> TRUE 0.036038532 0.091967865 0.103541838 0.122375886
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.813565921 0.766384317 0.709847579 0.642056833
#> TRUE 0.186434079 0.233615683 0.290152421 0.357943167
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.534680042 0.420163581
#> TRUE 0.465319958 0.579836419
#>
#> , , nivelaprob = Prepa, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.944777096 0.863297125 0.847041683 0.821013569
#> TRUE 0.055222904 0.136702875 0.152958317 0.178986431
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.736228599 0.677239623 0.610104736 0.534298848
#> TRUE 0.263771401 0.322760377 0.389895264 0.465701152
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.423615654 0.316696912
#> TRUE 0.576384346 0.683303088
#>
#> , , nivelaprob = Tec/Prof, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.921142096 0.811738254 0.790837325 0.757977897
#> TRUE 0.078857904 0.188261746 0.209162675 0.242022103
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.655849748 0.588921937 0.516530979 0.439253245
#> TRUE 0.344150252 0.411078063 0.483469021 0.560746755
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.334132606 0.240379912
#> TRUE 0.665867394 0.759620088
#>
#> , , nivelaprob = Maestría/Doc, sexojefe = 1
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.859062764 0.692302373 0.663636147 0.620385722
#> TRUE 0.140937236 0.307697627 0.336363853 0.379614278
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.498603489 0.427776466 0.357945739 0.290154726
#> TRUE 0.501396511 0.572223534 0.642054261 0.709845274
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.207511367 0.141724852
#> TRUE 0.792488633 0.858275148
#>
#> , , nivelaprob = No esp, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.932386455 0.880734740 0.700279587 0.645334172
#> TRUE 0.067613545 0.119265260 0.299720413 0.354665828
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.633987298 0.556477642 0.449712757 0.330816692
#> TRUE 0.366012702 0.443522358 0.550287243 0.669183308
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.230411456 0.155807807
#> TRUE 0.769588544 0.844192193
#>
#> , , nivelaprob = Ninguna/Pre, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.995073840 0.990840160 0.971610831 0.963837858
#> TRUE 0.004926160 0.009159840 0.028389169 0.036162142
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.962082189 0.948397169 0.922904918 0.878662448
#> TRUE 0.037917811 0.051602831 0.077095082 0.121337552
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.814320008 0.729987886
#> TRUE 0.185679992 0.270012114
#>
#> , , nivelaprob = Primaria, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.990070973 0.981617119 0.944117781 0.929364447
#> TRUE 0.009929027 0.018382881 0.055882219 0.070635553
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.926063486 0.900720320 0.855269565 0.781406472
#> TRUE 0.073936514 0.099279680 0.144730435 0.218593528
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.684036750 0.571657800
#> TRUE 0.315963250 0.428342200
#>
#> , , nivelaprob = Secundaria, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.985887156 0.973964755 0.922094209 0.902129225
#> TRUE 0.014112844 0.026035245 0.077905791 0.097870775
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.897695605 0.864056207 0.805445966 0.714639295
#> TRUE 0.102304395 0.135943793 0.194554034 0.285360705
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.602652172 0.483196476
#> TRUE 0.397347828 0.516803524
#>
#> , , nivelaprob = Prepa, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.978109421 0.959883821 0.883320342 0.854981485
#> TRUE 0.021890579 0.040116179 0.116679658 0.145018515
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.848770080 0.802581078 0.725875232 0.615651774
#> TRUE 0.151229920 0.197418922 0.274124768 0.384348226
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.492409774 0.374225665
#> TRUE 0.507590226 0.625774335
#>
#> , , nivelaprob = Tec/Prof, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.968261161 0.942319654 0.837895369 0.801009213
#> TRUE 0.031738839 0.057680346 0.162104631 0.198990787
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.793045649 0.735147956 0.643867548 0.522367075
#> TRUE 0.206954351 0.264852044 0.356132452 0.477632925
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.398440396 0.289927685
#> TRUE 0.601559604 0.710072315
#>
#> , , nivelaprob = Maestría/Doc, sexojefe = 2
#>
#> decil
#> vehiculo [ 0.00, 9.05) [ 9.05, 9.40) [ 9.40, 9.66) [ 9.66, 9.88)
#> FALSE 0.940895291 0.895011771 0.729524573 0.677471173
#> TRUE 0.059104709 0.104988229 0.270475427 0.322528827
#> decil
#> vehiculo [ 9.88,10.08) [10.08,10.28) [10.28,10.51) [10.51,10.76)
#> FALSE 0.666621315 0.591570368 0.485441837 0.363336610
#> TRUE 0.333378685 0.408429632 0.514558163 0.636663390
#> decil
#> vehiculo [10.76,11.14) [11.14,14.35]
#> FALSE 0.256849716 0.175639444
#> TRUE 0.743150284 0.824360556
fit_enigh_b[['decil']] <- tab_decil