5.2 Mecanismos de faltantes
A continuación consideramos cuatro mecanismos que dan lugar a datos faltantes. Para dar un ejemplo de cada caso, consideramos el escenario de una encuesta donde se pregunta el ingreso del hogar.
Decimos que el mecanismo de censura es MCAR (missing completely at random, o faltante totalmente al azar) cuando se cumple \[p_{\phi}(I|y_{obs},y_{falta})=p_{\phi}(I). \] Esto es, una variable es MCAR si la probabilidad de faltar es la misma para todas las unidades. Por ejemplo, si todos los encuestados deciden si contestar la pregunta de ingresos lanzando un dado y negansdose a contestar si observa un 6. En el caso MCAR eliminar las observaciones con faltantes no genera un sesgo en la inferencia.
Decimos que el mecanismo de censura es MAR (missing at random o faltante al azar) cuando \[p_{\phi}(I|y_{obs},y_{falta})=p_{\phi}(I|y_{obs}), \] es decir, la probabilidad de censura de una una variable dada no depende de los valores que toma esa variable, pero puede depender de otros datos observados. En la mayor parte de los casos los faltantes no cumplen MCAR. Por ejemplo, la tasa de no respuesta suele diferir entre blancos y negros, esto es un indicador de que la pregunta ingresos no cumple los supuestos de MCAR.
El supuesto de MAR es más general, por ejemplo si observamos genero, raza, educación y edad para todos los encuestados, enotnces ingresos es MAR si la porbabilidad de no-respuesta para esta pregunta depende únicamente de estas variables completamente observada.- En otro caso, decimos que el mecanismo de censura es MNAR (missing not at random). Notemos que faltantes dejan de ser aleatorios cuando dependen de información que no se colectó. Por ejemplo, es común que en ensayos clínicos si un tratamiento particular causa molestias los pacinetes son más propensos a abandonar el estudio, y dado que se busca medir la eficacia de cada tratamiento tenemos faltantes no aleatorios. Otro caso de falatantes no aleatorios es cuando la probabilidad de que cierta variable falte depende de la variable misma. Por ejemplo, supongamos que la gente con mayor ingreso es menos propensa a revelarlo. El caso extremo (por ejemplo, todas las personas con ganancia mayor a $100,000 se rehusan a contestar) se conoce como censura. Cuando tenemos MNAR es necesario modelar el mecanismo de datos faltantes, o aceptar que nuestros resultados serán sesgados.
Ejemplo. En nuestro ejemplo de las monedas, los faltantes de soles son MCAR, mientras que los faltantes de monedas son sólo MAR, pues la probabilidad de censura cambia con el valor del volado. Los procesos de censura de cada variable son independientes, así que estos datos son MAR.
Más adelante discutimos estos supuestos. Nótese que si se cumple MAR, entonces tenemos que \[p_{\theta,\psi} (y_{obs},I)= p_{\psi}(I|y_{obs})\int p_{\theta} (y_{obs}, y_{falta})dy_{falta}.\]
Lo interesante de esta expresión es que los parámetros \(\psi\) y \(\theta\) están en factores separados. Esto implica que para maximizar el lado izquierdo, hay que maximizar por separado los dos factores. Más interesante es que para encontrar los estimadores de máxima verosimilitud, no es necesario trabajar con \(\psi\) ni el mecanismo al azar. Esto es, el mecanismo de faltantes es ignorable. En otras palabras,
Si el mecanismo de censura es MAR, podemos maximizar verosimilitud simplemente maximizando la verosimilitud completa donde los valores censurados están integrados respecto a la condicional de modelo de los datos. El cumplimiento de MAR depende del fenómeno que produce los datos y del modelo que estamos usando.
Ejemplo. Ahora podemos escribir la función de log verosimilitud para nuestro problema de arriba. Para una observación en particular, tenemos:
Si tenemos el valor de sol=1, y la moneda está censurada, entonces marginalizando (no es integral en este caso, es una suma): \[p_\theta(sol=1)=\theta\theta_A + \theta\theta_B,\] y \[p_\theta(sol=0)=\theta(1-\theta_A) + \theta(1-\theta_B),\]
Si tenemos el valor de moneda y el sol está censurado, entonces la probabilidad de la observación es \(\theta\) (moneda A) o \(1-\theta\) (moneda B).
Si ambos valores están censarados, entonces el caso contribuye 0 a la log verosimilitud.
logLikObs <- function(moneda, sol, theta){
salida <- 1
if(is.na(moneda) & !is.na(sol)){
salida <- (theta[1] * (sol * theta[2] + (1 - sol) * theta[2]) +
(1 - theta[1]) * (sol * theta[3] + (1 - sol) * theta[3]))
}
if(is.na(sol) & !is.na(moneda)){
salida <- ((moneda == 'A') * theta[1] + (moneda == 'B') * (1 - theta[1]))
}
if(!is.na(sol) & !is.na(moneda)){
parte_1 <- (theta[1] * (moneda == 'A') + (1 - theta[1]) * (moneda == 'B'))
parte_2 <- (ifelse(moneda == 'A', sol * theta[2] +
(1 - sol) * (1 - theta[2]), sol * theta[3] +
(1 - sol) * (1 - theta[3])))
salida <- parte_1 * parte_2
}
log(salida)
}
logData <- function(datos){
function(theta){
suma <- sapply(1:nrow(datos), function(i){
logLikObs(moneda = datos[i, 'moneda'], sol = datos[i, 'sol'], theta)
})
sum(suma)
}
}
func_1 <- logData(datos_L_obs)
optim(c(0.5, 0.6, 0.3), func_1, control = list(fnscale = -1))
#> $par
#> [1] 0.4836783 0.5204267 0.3329634
#>
#> $value
#> [1] -1124.02
#>
#> $counts
#> function gradient
#> 72 NA
#>
#> $convergence
#> [1] 0
#>
#> $message
#> NULLComparamos con el caso en que eliminamos faltantes y hacemos conteos:
prop.table(table(datos_L_obs$moneda))
#>
#> A B
#> 0.4712644 0.5287356
prop.table(table(datos_L_obs$moneda, datos_L_obs$sol), margin=1)
#>
#> 0 1
#> A 0.5682540 0.4317460
#> B 0.7385445 0.2614555En R, el paquete catnet permite el aprendizaje y estimación de redes con datos faltantes.
Ejemplo: MAR, MCAR, MNAR. Consideramos los siguientes datos completos, donde cada renglón representa a un empleado, IQ es una medición que se le hizo al empleado cuando fue contratado, y performance es una evaluación de desempeño a 6 meses de su contratación. Los datos completos están dados por la tercera columna (performance).
datos_cens <- read.csv(file = 'data/ejemplos_censurados.csv')
datos_cens[, c('IQ', 'performance')]
#> IQ performance
#> 1 78 9
#> 2 84 13
#> 3 84 10
#> 4 85 8
#> 5 87 7
#> 6 91 7
#> 7 92 9
#> 8 94 9
#> 9 94 11
#> 10 96 7
#> 11 99 7
#> 12 105 10
#> 13 105 11
#> 14 106 15
#> 15 108 10
#> 16 112 10
#> 17 113 12
#> 18 115 14
#> 19 118 16
#> 20 134 12Ahora consideramos tres escenarios que podrían resultar en datos faltantes de la variable performance:
En un accidente, los archivos de desempeño de empleados cuyo apellido que comienza con las letras A-C se pierden.
Los empleados con medidas más bajas de IQ de no se contratan, así que no se observa su desempeño.
Los empleados con peor desempeño (apreciativo, que correlaciona con la evaluación formal) son despedidos antes de los 6 meses de la evaluación de desempeño formal.
Podríamos obtener datos como sigue:
datos_cens
#> case IQ performance performance.MCAR performance.MAR performance.MNAR
#> 1 1 78 9 9 NA NA
#> 2 2 84 13 13 NA 13
#> 3 3 84 10 NA NA 10
#> 4 4 85 8 8 NA NA
#> 5 5 87 7 7 NA NA
#> 6 6 91 7 7 NA NA
#> 7 7 92 9 NA NA NA
#> 8 8 94 9 9 9 NA
#> 9 9 94 11 11 11 11
#> 10 10 96 7 7 7 NA
#> 11 11 99 7 7 7 NA
#> 12 12 105 10 10 10 10
#> 13 13 105 11 NA 11 11
#> 14 14 106 15 NA 15 15
#> 15 15 108 10 10 10 10
#> 16 16 112 10 10 10 10
#> 17 17 113 12 12 12 12
#> 18 18 115 14 14 14 14
#> 19 19 118 16 16 16 16
#> 20 20 134 12 NA 12 12Consideramos cómo es el mecanismo de censura para la variable performance bajo los distintos escenarios:
MCAR: En el primer escenario, la letra del primer apellido no correlaciona con IQ o performance. Los faltantes de performance tienen una probabilidad fija de ocurrir, que no depende de ninguna otra variable. Este es el caso de la columna peformance.MCAR.
MAR: En el segundo escenario, la aparición de performance depende del IQ, que siempre es observado. Pero una vez que condicionamos a IQ, no está relacionada con los valores que toma performance.MAR.
MNAR En el último caso, los faltantes de performance.MNAR dependen tanto de performance y de IQ. Este es el caso MNAR.
Los datos se ven como sigue en cada caso:
library(plyr)
library(tidyr)
library(dplyr)
library(ggplot2)
datos_cens_l <- datos_cens %>%
gather(type_miss, value, performance.MCAR:performance.MNAR)
ggplot(datos_cens_l, aes(x = IQ, y = performance)) +
geom_point(colour = "red", size = 1.5) +
geom_point(aes(x = IQ, y = value, group = type_miss), size = 1.5) +
geom_smooth(aes(x = IQ, y = value, group = type_miss), color = "black",
method = "lm", se = TRUE) +
geom_smooth(method = "lm", se = FALSE, color = "red") +
facet_wrap(~ type_miss) +
labs(title = "Mecanismos de datos faltantes")
datos_cens %>%
gather(type_miss, value, performance:performance.MNAR) %>%
group_by(type_miss) %>%
summarise(
media = mean(value, na.rm = TRUE),
se = sd(value, na.rm = TRUE)
)
#> media se
#> 1 10.75 2.652948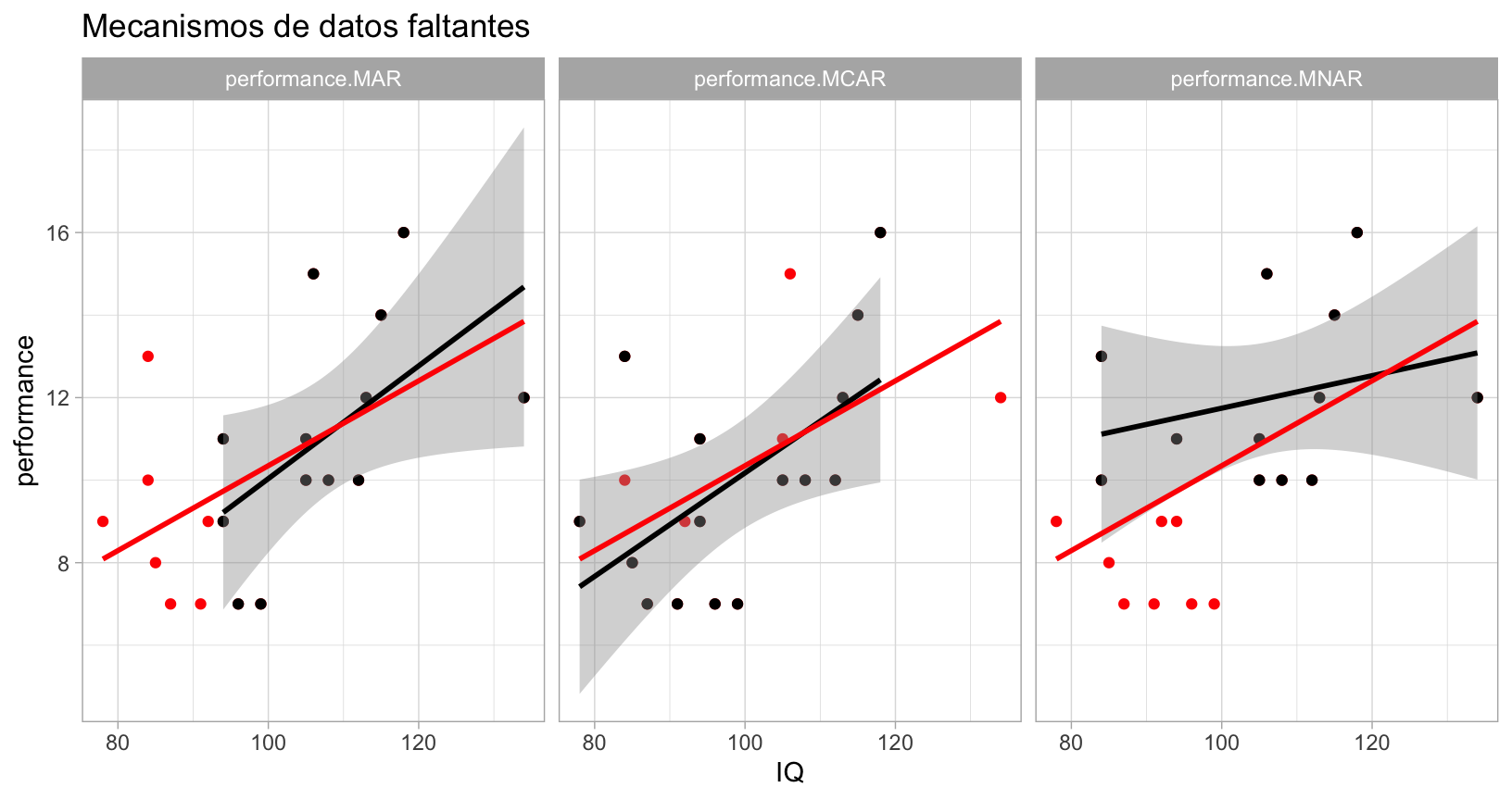
De las figuras de arriba notemos que en MCAR podemos eliminar datos (aunque no
sea lo más eficiente) sin producir sesgos en la estimación condicional de
performance dado IQ.
Bajo MAR, eliminar casos faltantes produce sesgos en la estimación de la media y varianza, y posiblemente atenúa la correlación (al eliminar observaciones de una cola).
Finalmente, bajo MNAR, eliminar casos faltantes produce sesgos en estimación de media, varianza y los coeficientes de regresión:
5.2.1 Métodos usuales de imputación
En un proceso de imputación, buscamos imputar datos faltantes de manera que podamos usar métodos de datos completos. Esta imputación funciona bien cuando no altera de manera considerable las características distribucionales de los datos.
A continuación usamos el ejemplo para mostrar algunos métodos de imputación.
Media. Podemos hacer imputación con la media, que en este caso distorsiona la relación entre IQ y performance (jalándola hacia cero). También afecta la estimación de la media de performance y deriva en subestimar el error estándar de la variable.
datos_cens$performance_imp_media <- datos_cens$performance.MAR
datos_cens$performance_imp_media[is.na(datos_cens$performance.MAR)] <-
mean(datos_cens$performance.MAR, na.rm = T)
# Media y desviación estándar
c(mean(datos_cens$performance_imp_media), sd(datos_cens$performance_imp_media))
#> [1] 11.076923 2.187561
ggplot(datos_cens, aes(x = IQ, y = performance)) +
geom_point(color = "red", size = 1.5) +
geom_point(aes(y = performance_imp_media, color = is.na(performance.MAR)),
size = 1.5) +
scale_color_manual(name = "Imputados", values = c("darkgray", "purple")) +
geom_smooth(aes(y = performance_imp_media), method ='lm', se = FALSE,
color = "darkgray")+
geom_smooth(aes(y = performance), colour = 'red', se = FALSE, method ='lm')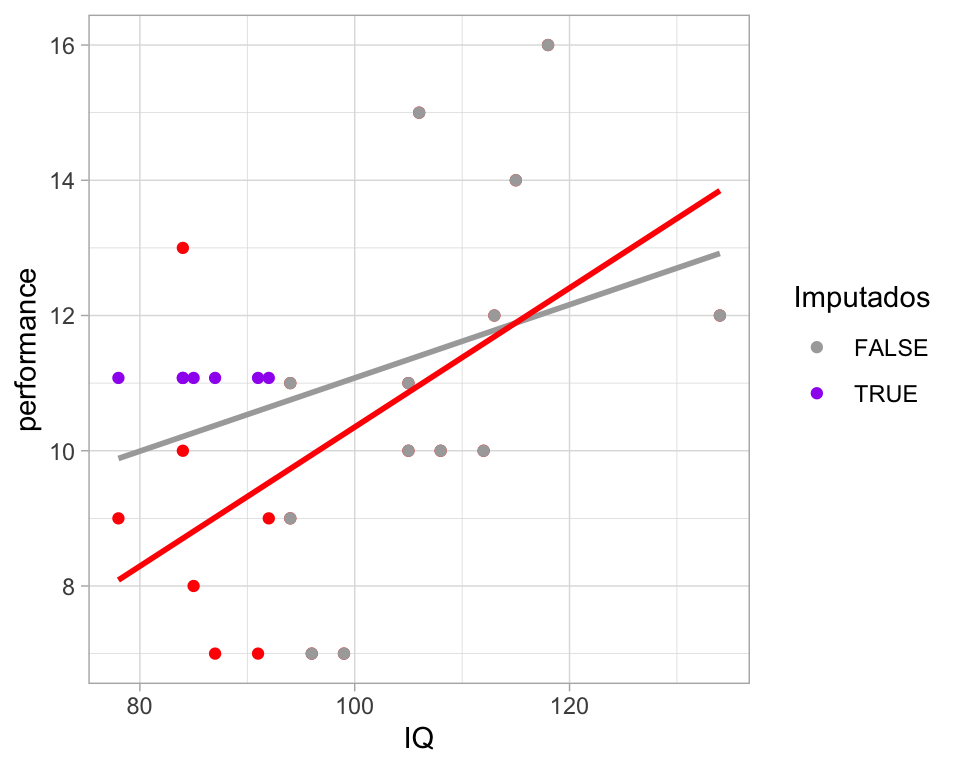
Regresión. Otro enfoque es imputación simple con regresión: ajustamos un modelo de performance vs IQ, e imputamos con las predicciones del modelo:
library(arm)
datos_cens$performance_imp_lm <- datos_cens$performance.MAR
mod_1 <- lm(performance.MAR ~ IQ, data = datos_cens)
display(mod_1)
#> lm(formula = performance.MAR ~ IQ, data = datos_cens)
#> coef.est coef.se
#> (Intercept) -3.63 6.67
#> IQ 0.14 0.06
#> ---
#> n = 13, k = 2
#> residual sd = 2.39, R-Squared = 0.31
datos_cens$performance_imp_lm[is.na(datos_cens$performance.MAR)] <-
predict(mod_1, newdata = subset(datos_cens, is.na(performance.MAR)))
# Media y desviación estándar
c(mean(datos_cens$performance_imp_lm), sd(datos_cens$performance_imp_lm))
#> [1] 10.036336 2.652309
ggplot(datos_cens, aes(x = IQ, y = performance)) +
geom_point(color = "red", size = 1.5) +
geom_point(aes(y = performance_imp_lm, color = is.na(performance.MAR)),
size = 1.5) +
scale_color_manual(name = "Imputados", values = c("darkgray", "purple")) +
geom_smooth(aes(y = performance_imp_lm), method ='lm', se = FALSE,
color = "darkgray")+
geom_smooth(aes(y = performance), colour = 'red', se = FALSE, method ='lm')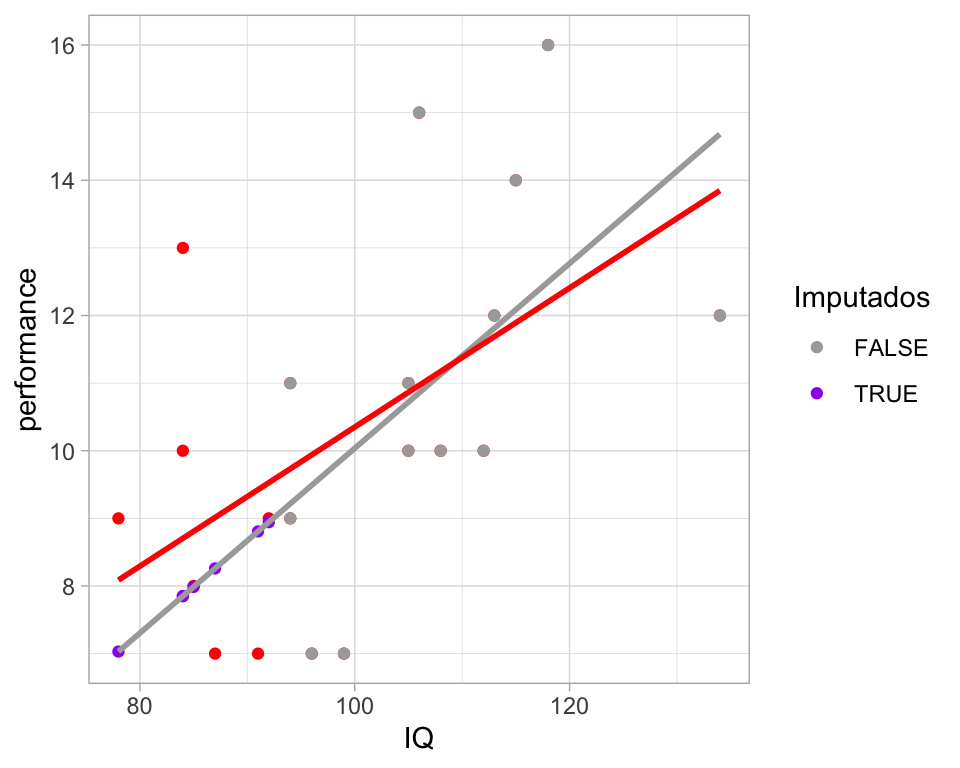
En este caso, agregamos observaciones que tienen correlación perfecta, notemos que \(R^2=0.24\) lo que quiere decir que la varianza explicada en la regresión es únicamente el \(0.24%\) de la varianza total, por tanto los valores de predicción tienden a ser menos variables que los datos originales.
Estocástica con regresión. Podemos regresar la incertidumbre a las imputaciones sumando el error de predicción. La idea es simular observaciones bajo el modelo:
datos_cens$performance_imp_st <- datos_cens$performance.MAR
pred_1 <- predict(mod_1, newdata = subset(datos_cens, is.na(performance.MAR)))
display(mod_1)
#> lm(formula = performance.MAR ~ IQ, data = datos_cens)
#> coef.est coef.se
#> (Intercept) -3.63 6.67
#> IQ 0.14 0.06
#> ---
#> n = 13, k = 2
#> residual sd = 2.39, R-Squared = 0.31
datos_cens$performance_imp_st[is.na(datos_cens$performance.MAR)] <- pred_1 +
rnorm(sum(is.na(datos_cens$performance.MAR)), 0, sd = 2.39)
ggplot(datos_cens, aes(x = IQ, y = performance)) +
geom_point(color = "red", size = 1.5) +
geom_point(aes(y = performance_imp_st, color = is.na(performance.MAR)),
size = 1.5) +
scale_color_manual(name = "Imputados", values = c("darkgray", "purple")) +
geom_smooth(aes(y = performance_imp_st), method ='lm', se = FALSE,
color = "darkgray")+
geom_smooth(aes(y = performance), colour = 'red', se = FALSE, method ='lm')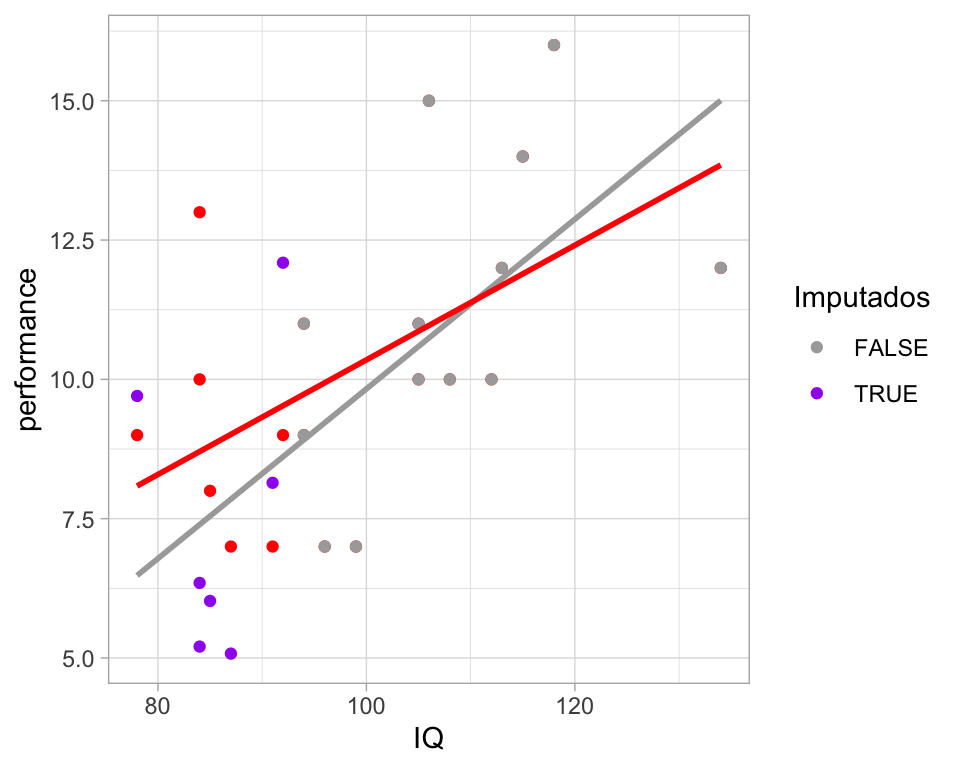
Nótese que nuestro proceso produce conjuntos de datos más similares a los datos originales. En el ejemplo siguiente, hacemos cinco imputaciones estocásticas y comparamos con los datos completos:
repImp <- function(rep){
originales <- datos_cens$performance.MAR
num_faltantes <- sum(is.na(originales))
faltantes_imp <- pred_1 + rnorm(num_faltantes, 0, sd = 2.39)
originales[is.na(originales)] <- faltantes_imp
data.frame(performance = originales, IQ = datos_cens$IQ)
}
imp_rep <- rdply(5, repImp)
orig_1 <- dplyr::select(datos_cens, IQ, performance) %>%
mutate(.n = 'completos')
ggplot(imp_rep, aes(x = IQ, y = performance, group = .n)) +
geom_smooth(se=FALSE, method = "lm", color = "darkgray") +
geom_point(data = orig_1, colour='red', size = 1.5,
aes(x = IQ, y = performance)) +
geom_smooth(data = orig_1, colour='red', method = "lm", se = FALSE,
aes(x = IQ, y = performance))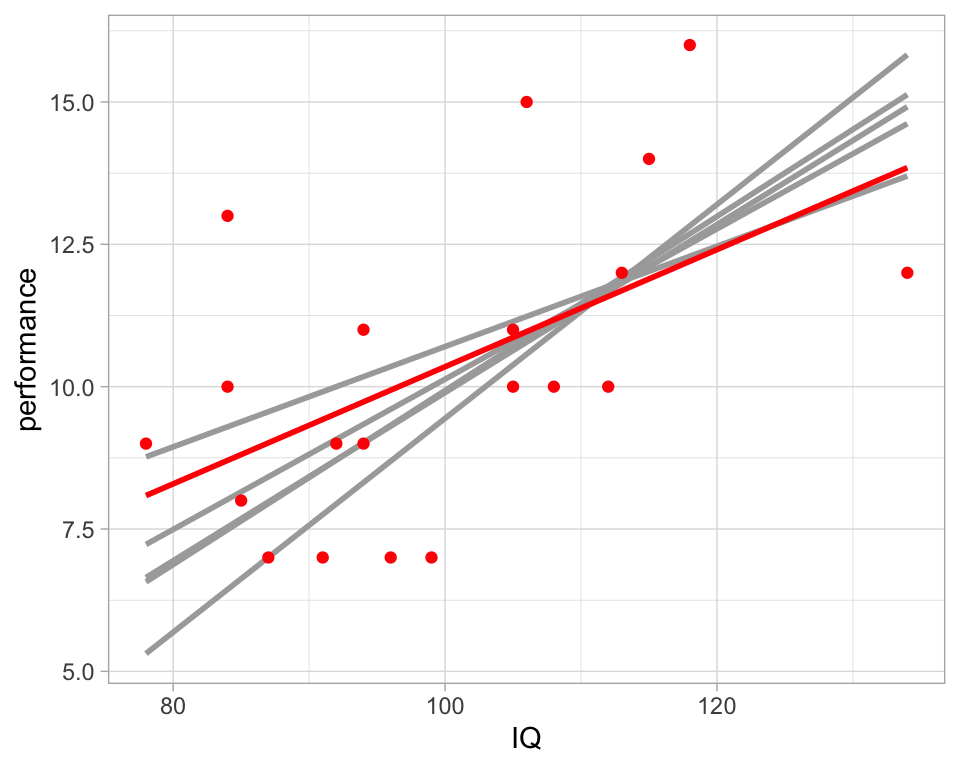
 Repite la imputación estocástica
para los faltantes MCAR y MNAR.
Repite la imputación estocástica
para los faltantes MCAR y MNAR.
En la siguiente tabla consideramos un ejercicio de simulación, donde se hicieron distintas imputaciones para cada proceso de censura. En esta tabla vemos que en caso MAR, el único método insesgado es imputación estocástica con regresión. Todos los demás métodos introducen sesgos. Por otra parte, ningún método funciona bien para MNAR.
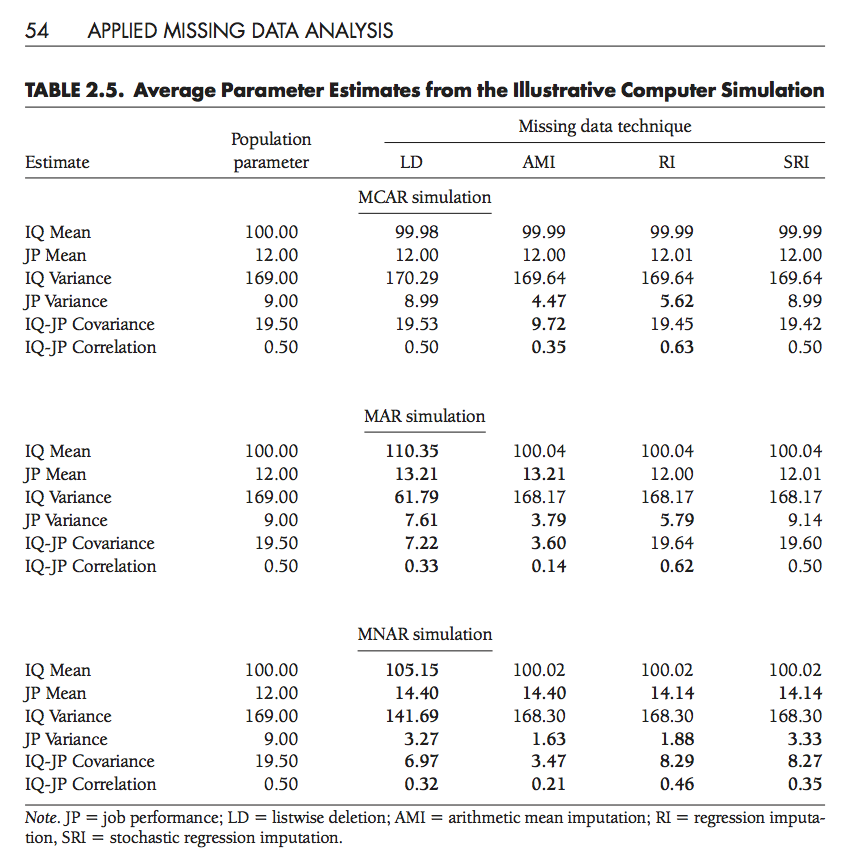
Para imputación bajo MAR, usamos métodos estocásticos basados en modelos para la variable que queremos imputar en términos de otras observadas. Es importante incluir todas las variables que influyen en la censura o no respuesta.
Típicamente hacemos unas pocas replicaciones (por ejemplo 5) de la imputación, y verificamos los resultados de nuestro análisis a lo largo de las 5 imputaciones distintas.
5.2.2 Verificación de MAR
Como discutimos antes, los faltantes al azar son más fáciles de manejar; sin embargo, en general no podemos estar seguros de que los faltantes dependen de predictores no observados o de las variables mismas en que observamos los faltantes. En general debemos realizar supuestos, o revisar estudios similares. En la práctica se intenta incluir los más predictores posibles de tal manera que que el supuesto de MAR sea razonable. Por ejemplo, puede ser un supuesto muy fuerte decir que la no respuesta a la pregunta de ingresos depende únicamente de género, raza y educación, pero es mucho más razonable que suponer que la probabilidad de no respuesta es constante o que depende únicamente de uno de los predictores propuestos.
No es posible hacer pruebas para confirmar MAR en lugar de MNAR. La razón es precisamente que los datos que necesitamos para ver la posibilidad de MNAR están censurados.
El enfoque tanto de máxima verosimilitud como de imputación consiste en incluir suficientes variables en el modelo, todas observadas, de manera que estas variables expliquen las probabilidades de censura, y así la probabilidad de faltantes no dependa de la variable de interés.
- El caso MNAR es más difícil, pues en este caso típicamente el mecanismo de censura no es ignorable: tenemos que modelarlo. Esto es más complicado técnicamente y generalmente no tenemos información razonable para construir estos modelos.