8.1 Análisis de datos de variación continua
\(Y(s)\) es un vector aleatorio en una ubicación \(s \in \mathbb{R}^r\) donde \(s\) varía de manera continua sobre el dominio \(\mathcal{D} \subset \mathbb{R}^r\) (usualmente r= 2).
Si consideramos un número finito de ubicaciones \(\{s_1,...,s_n\} \in \mathcal{D}\) entonces \((Y(s_1),...,Y(s_n))\) es un vector aleatorio de dimensión \(n\) cuya distribución debe reflejar la dependencia espacial entre las variables. Si observamos datos \(y_1,...,y_n\) en las ubicaciones \(s_1,...,s_n\) entonces \(y_1,...,y_n\) es una realización del vector aleatorio \((Y(s_1),...,Y(s_n))\).
Ahora, para especificar la distribución del proceso espacial utilizaremos las distribuciones finito dimensionales: \[p_{s_1,...,s_n}(y_1,...,y_n)\] para toda \(n \geq 1\) y para todo \(s_1,...,s_n \in \mathcal{D}\).
Las distribuciones finito-dimensionales definen una distribución válida sobre el proceso estocástico espacial \(\{Y(s):s\in \mathcal{D}\}\) si satisfacen las siguientes condiciones (compatibilidad de Kolmogorov):
Son invariantes ante permutaciones.
Son consistentes bajo marginalización.
Un ejemplo de un proceso espacial que satisface las propiedades anteriores es el proceso Gaussiano.
\(\{Y(s):s\in \mathcal{D}\}\) es un proceso Gaussiano si para toda \(n \geq 1\) y \(s_1,...,s_n \in \mathcal{D}\) la distribución de \((Y(s_1),...,Y(s_n))\) es normal multivariada.
Para especificar un proceso Gausiano sólo hace falta especificar las medias y las matrices de covarianza para las distribuciones finito dimensionales. Más aún en el caso del proceso Gaussiano la condición de consistencia de Kolmogorov se reduce a que la matriz de covarianzas sea semidefinida positiva.
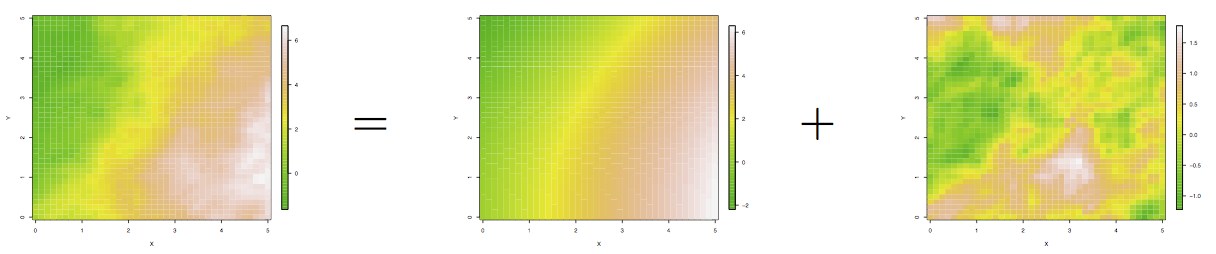
En general para especificar un proceso espacial \(Y(s)\) lo descomponemos en dos partes (primera ley de la geoestadística):
\[Y(s) = \mu(s) + \eta(s)\]
donde
\(\mu(s)\) es la media de \(Y(s)\). Es una función determinística de \(s\) y se le llama la tendencia espacial. Explica la variación a gran escala en el proceso espacial \(Y(s)\).
\(\eta(s)\) explica la varianza a pequeña escala del proceso \(Y(s)\). Tiene media cero en cada \(s\) y explica la dependencia espacial en \(Y(s)\) a través de la función de covarianza.
