4.3 Aprendizaje de estructura
Igual que en modelos log-lineales para datos categóricos, podemos ajustar modelos hacia atrás y hacia adelante (agregando/eliminando aristas) usando el BIC/AIC como criterio de selección, con distintas restricciones sobre la matriz de precisión.
Ejemplo
En este ejemplo consideramos las estaturas de los dos padres y de dos de sus hijas seleccionados al azar (entre las familias que tienen al menos dos hijas).
#> Observations: 232
#> Variables: 10
#> $ family <fct> 001, 001, 002, 002, 004, 004, 005, 005, 007, 007…
#> $ father <dbl> 78.5, 78.5, 75.5, 75.5, 75.0, 75.0, 75.0, 75.0, …
#> $ mother <dbl> 67.0, 67.0, 66.5, 66.5, 64.0, 64.0, 58.5, 58.5, …
#> $ midparentHeight <dbl> 75.43, 75.43, 73.66, 73.66, 72.06, 72.06, 69.09,…
#> $ children <int> 4, 4, 4, 4, 5, 5, 6, 6, 6, 6, 3, 3, 8, 8, 9, 9, …
#> $ childNum <int> 2, 3, 4, 3, 4, 3, 4, 6, 6, 5, 3, 2, 5, 3, 8, 6, …
#> $ gender <fct> female, female, female, female, female, female, …
#> $ childHeight <dbl> 69.2, 69.0, 65.5, 65.5, 64.5, 67.0, 66.5, 62.5, …
#> $ n_female <int> 3, 3, 2, 2, 3, 3, 3, 3, 2, 2, 3, 3, 6, 6, 4, 4, …
#> $ id <int> 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, …
#> father mother h1 h2
#> father 7.1720502 -0.1878066 2.177559 3.0108231
#> mother -0.1878066 4.6606747 1.121364 0.9641169
#> h1 2.1775592 1.1213643 4.773493 2.0603988
#> h2 3.0108231 0.9641169 2.060399 5.1546777
#> father mother h1 h2
#> father 0.20108445 0.04317091 -0.05763349 -0.10249012
#> mother 0.04317091 0.23951281 -0.05527503 -0.04791953
#> h1 -0.05763349 -0.05527503 0.27768198 -0.06699154
#> h2 -0.10249012 -0.04791953 -0.06699154 0.28960277
#> change.AIC -30.6315 Edge added: father h2
#> change.AIC -19.9684 Edge added: h2 h1
#> change.AIC -4.7490 Edge added: h1 mother
#> change.AIC -3.2652 Edge added: father h1
#> change.AIC -0.1072 Edge added: father mother
#> change.AIC -1.9052 Edge added: h2 mother
#> No edges can be added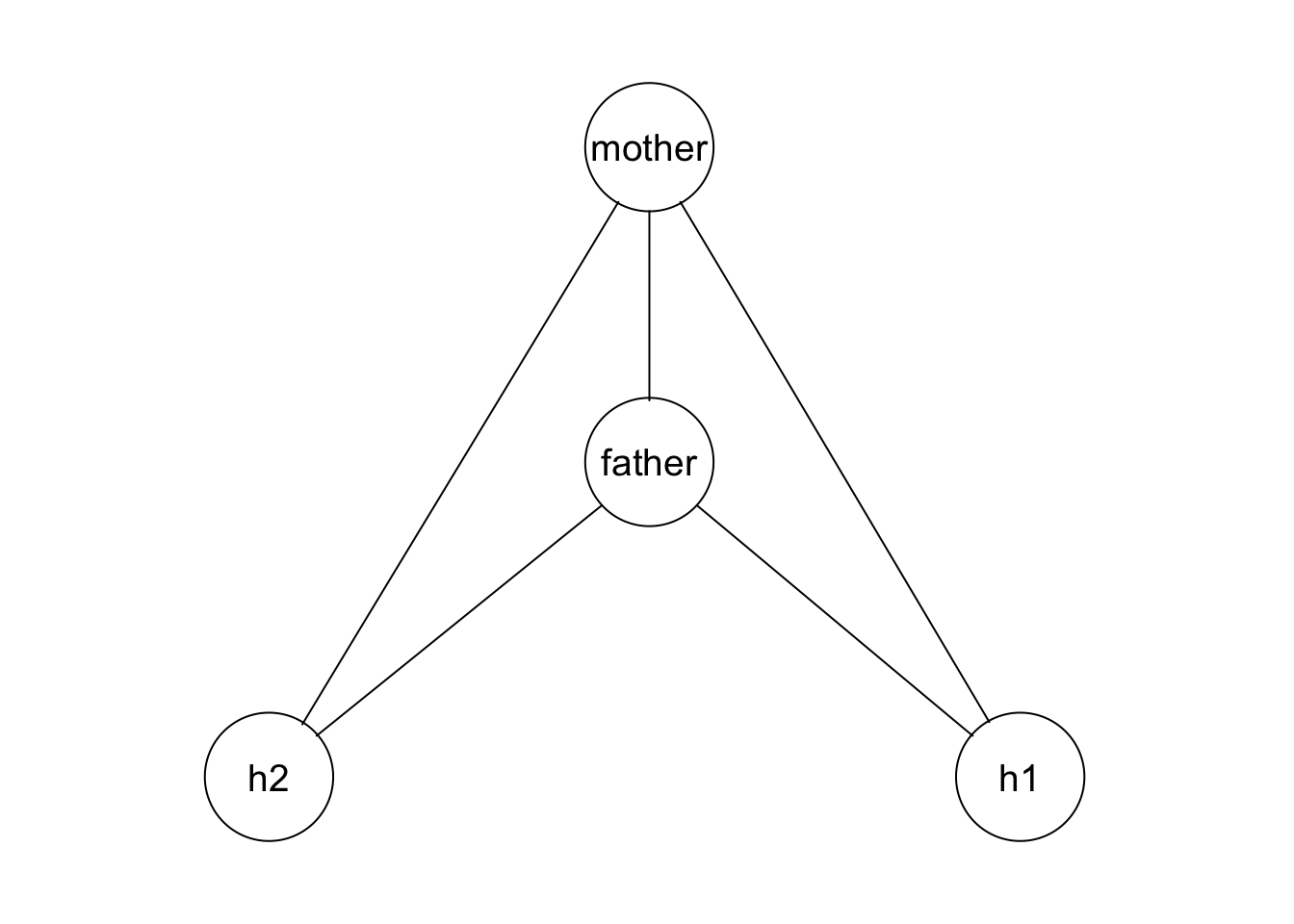
Podemos examinar la matriz de precisión ajustada:
D <- mod_hijas$fitinfo$K
D
#> father mother h1 h2
#> father 0.21622235 0.05274096 -0.08204905 -0.11740648
#> mother 0.05274096 0.24743880 -0.06693692 -0.06178743
#> h1 -0.08204905 -0.06693692 0.26446523 0.00000000
#> h2 -0.11740648 -0.06178743 0.00000000 0.27581862y para checar el ajuste comparamos la matriz de covarianzas empírica con la ajustada:
round(cor(dat_w), 2)
#> father mother h1 h2
#> father 1.00 -0.03 0.37 0.50
#> mother -0.03 1.00 0.24 0.20
#> h1 0.37 0.24 1.00 0.42
#> h2 0.50 0.20 0.42 1.00
round(cov2cor(solve(D)), 2)
#> father mother h1 h2
#> father 1.00 -0.03 0.37 0.50
#> mother -0.03 1.00 0.24 0.20
#> h1 0.37 0.24 1.00 0.24
#> h2 0.50 0.20 0.24 1.00Podemos comparar con
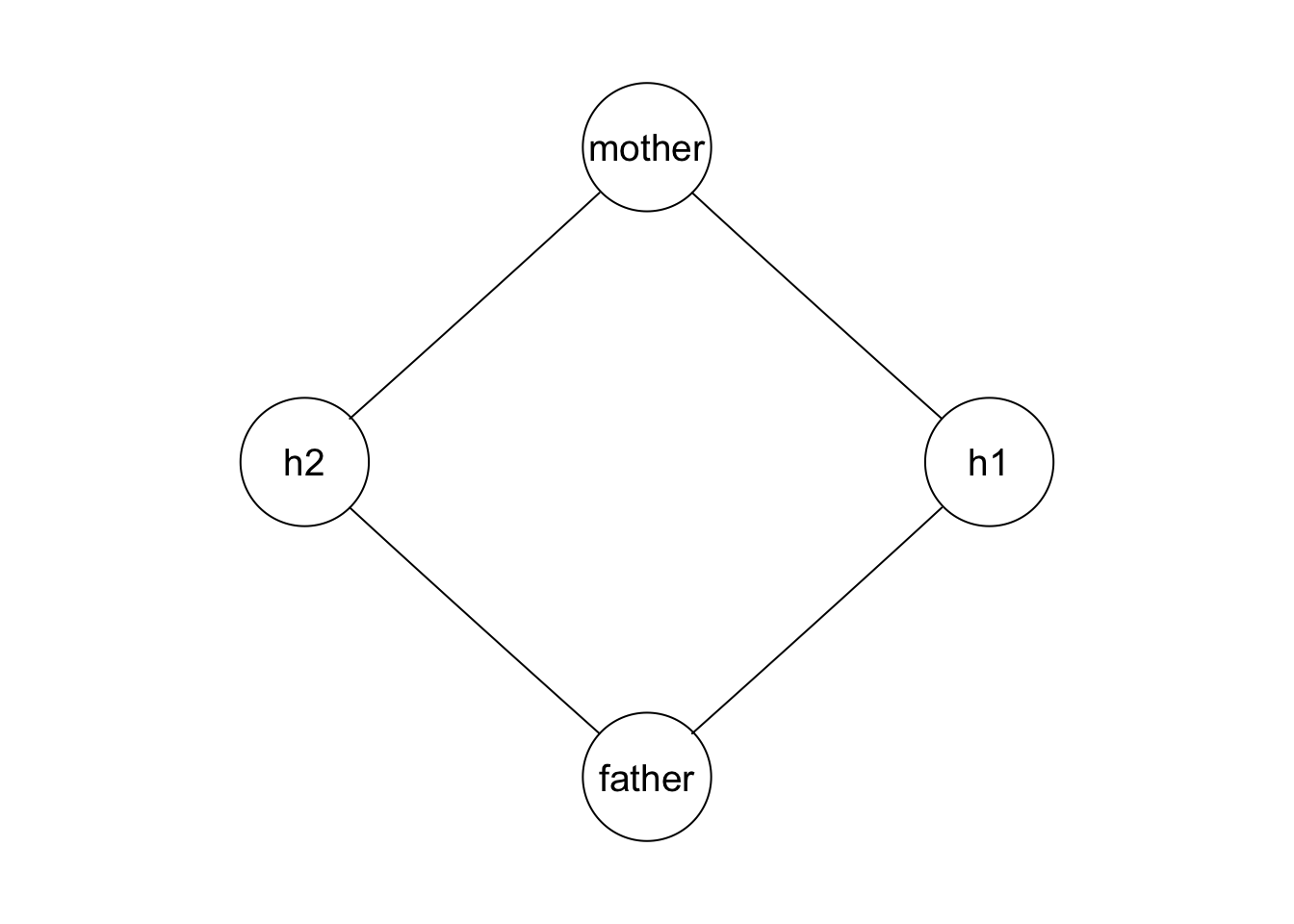
mod_hijas_2
#> Model: A cModel with 4 variables
#> -2logL : 2031.79 mdim : 8 aic : 2047.79
#> ideviance : 59.59 idf : 4 bic : 2069.82
#> deviance : 13.03 df : 2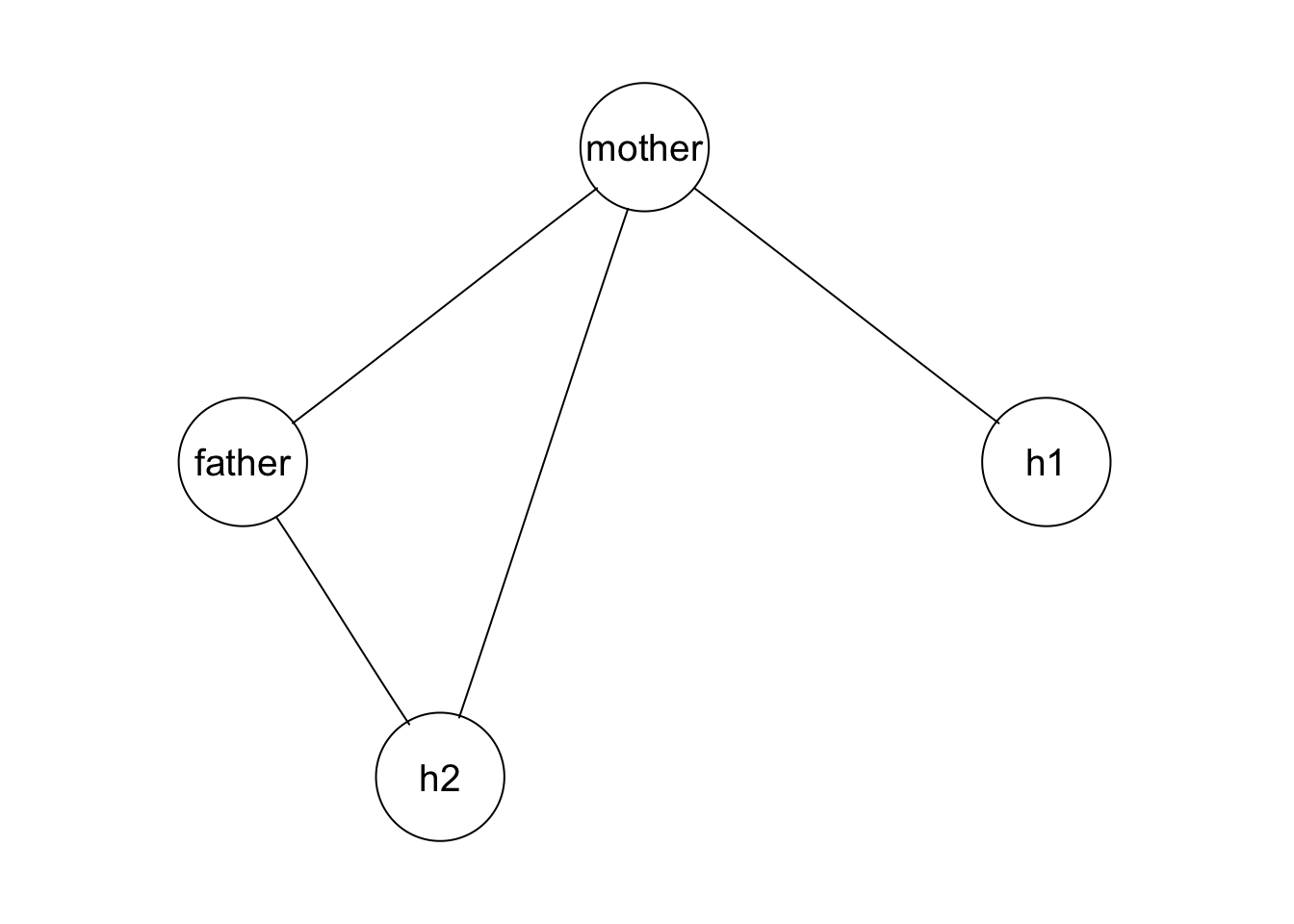
mod_hijas_3
#> Model: A cModel with 4 variables
#> -2logL : 2044.70 mdim : 8 aic : 2060.70
#> ideviance : 46.69 idf : 4 bic : 2082.73
#> deviance : 25.94 df : 2Nótese que la estimación de la matriz de varianza y covarianza está cercana a la empírica:
D <- mod_hijas_2$fitinfo$K
round(cor(dat_w), 2)
#> father mother h1 h2
#> father 1.00 -0.03 0.37 0.50
#> mother -0.03 1.00 0.24 0.20
#> h1 0.37 0.24 1.00 0.42
#> h2 0.50 0.20 0.42 1.00
round(cov2cor(solve(D)),2)
#> father mother h1 h2
#> father 1.00 0.15 0.37 0.50
#> mother 0.15 1.00 0.24 0.20
#> h1 0.37 0.24 1.00 0.21
#> h2 0.50 0.20 0.21 1.00Mientras que eliminar father-h1 muestra un desajuste más considerable:
D <- mod_hijas_3$fitinfo$K
round(cor(dat_w), 2)
#> father mother h1 h2
#> father 1.00 -0.03 0.37 0.50
#> mother -0.03 1.00 0.24 0.20
#> h1 0.37 0.24 1.00 0.42
#> h2 0.50 0.20 0.42 1.00
round(cov2cor(solve(D)),2)
#> father mother h1 h2
#> father 1.00 -0.03 -0.01 0.50
#> mother -0.03 1.00 0.24 0.20
#> h1 -0.01 0.24 1.00 0.05
#> h2 0.50 0.20 0.05 1.00Ejemplo: datos bodyfat
Consideramos varias mediciones de dimensiones corporales de un conjunto de hombres, más una medición adicional de grasa corporal. En este ejemplo ilustramos
bodyfat <- read.table('data/bodyfat.txt', header=T)
head(bodyfat)
#> densidad grasacorp edad peso estatura cuello pecho abdomen cadera
#> 1 1.0708 12.3 23 154.25 67.75 36.2 93.1 85.2 94.5
#> 2 1.0853 6.1 22 173.25 72.25 38.5 93.6 83.0 98.7
#> 3 1.0414 25.3 22 154.00 66.25 34.0 95.8 87.9 99.2
#> 4 1.0751 10.4 26 184.75 72.25 37.4 101.8 86.4 101.2
#> 5 1.0340 28.7 24 184.25 71.25 34.4 97.3 100.0 101.9
#> 6 1.0502 20.9 24 210.25 74.75 39.0 104.5 94.4 107.8
#> muslo rodilla tobillo biceps antebrazo muñeca
#> 1 59.0 37.3 21.9 32.0 27.4 17.1
#> 2 58.7 37.3 23.4 30.5 28.9 18.2
#> 3 59.6 38.9 24.0 28.8 25.2 16.6
#> 4 60.1 37.3 22.8 32.4 29.4 18.2
#> 5 63.2 42.2 24.0 32.2 27.7 17.7
#> 6 66.0 42.0 25.6 35.7 30.6 18.8
cov(bodyfat)
#> densidad grasacorp edad peso estatura
#> densidad 0.0003621955 -0.1573232 -0.06658709 -0.3322694 0.006823236
#> grasacorp -0.1573232461 70.0358161 30.73813951 150.6233770 -2.743345665
#> edad -0.0665870897 30.7381395 158.81140517 -4.7206863 -7.923045912
#> peso -0.3322694180 150.6233770 -4.72068630 863.7227188 33.185646699
#> estatura 0.0068232356 -2.7433457 -7.92304591 33.1856467 13.416512521
#> cuello -0.0218812047 9.9804446 3.47717068 59.3484415 2.259054259
#> pecho -0.1095188854 49.5715943 18.74622304 221.5487495 4.165407418
#> abdomen -0.1639594052 73.4047562 31.31005028 281.4105414 3.468333808
#> cadera -0.0830776437 37.4833827 -4.54407133 198.0990467 4.471300512
#> muslo -0.0552615965 24.5866287 -13.23835610 134.0321848 2.854389585
#> rodilla -0.0227224018 10.2667805 0.53236577 60.4732812 2.527020489
#> tobillo -0.0085443597 3.7725479 -2.24394802 30.5685871 1.643568583
#> biceps -0.0280083485 12.4719933 -1.56721527 71.0710897 2.299788939
#> antebrazo -0.0135232205 6.1112838 -2.16592519 37.4313430 1.692347278
#> muñeca -0.0057871457 2.7077651 2.51220357 20.0230357 1.101330393
#> cuello pecho abdomen cadera muslo
#> densidad -0.0218812 -0.1095189 -0.1639594 -0.08307764 -0.0552616
#> grasacorp 9.9804446 49.5715943 73.4047562 37.48338266 24.5866287
#> edad 3.4771707 18.7462230 31.3100503 -4.54407133 -13.2383561
#> peso 59.3484415 221.5487495 281.4105414 198.09904667 134.0321848
#> estatura 2.2590543 4.1654074 3.4683338 4.47130051 2.8543896
#> cuello 5.9093392 16.0842168 19.7664219 12.79944033 8.8786132
#> pecho 16.0842168 71.0729177 83.2546561 50.09398786 32.3032418
#> abdomen 19.7664219 83.2546561 116.2747453 67.52212294 43.3990680
#> cadera 12.7994403 50.0939879 67.5221229 51.32372225 33.7148321
#> muslo 8.8786132 32.3032418 43.3990680 33.71483210 27.5619963
#> rodilla 3.9422349 14.6292753 19.1715709 14.22821286 10.1189812
#> tobillo 1.9689831 6.9012967 8.2831730 6.78010814 4.8031730
#> biceps 5.3698678 18.5403673 22.3157963 16.00124265 12.0782067
#> antebrazo 3.0634971 9.8834672 10.9668891 7.88981408 6.0133632
#> muñeca 1.6903567 5.1958504 6.2398022 4.21420034 2.7382684
#> rodilla tobillo biceps antebrazo muñeca
#> densidad -0.0227224 -0.00854436 -0.02800835 -0.01352322 -0.005787146
#> grasacorp 10.2667805 3.77254790 12.47199330 6.11128375 2.707765130
#> edad 0.5323658 -2.24394802 -1.56721527 -2.16592519 2.512203567
#> peso 60.4732812 30.56858708 71.07108969 37.43134296 20.023035714
#> estatura 2.5270205 1.64356858 2.29978894 1.69234728 1.101330393
#> cuello 3.9422349 1.96898312 5.36986783 3.06349712 1.690356669
#> pecho 14.6292753 6.90129672 18.54036726 9.88346724 5.195850408
#> abdomen 19.1715709 8.28317302 22.31579634 10.96688911 6.239802220
#> cadera 14.2282129 6.78010814 16.00124265 7.88981408 4.214200341
#> muslo 10.1189812 4.80317302 12.07820670 6.01336321 2.738268355
#> rodilla 5.8168014 2.50010245 4.94556251 2.70917663 1.496220831
#> tobillo 2.5001024 2.87266363 2.48281256 1.43518592 0.895904952
#> biceps 4.9455625 2.48281256 9.12809508 4.14078907 1.782985676
#> antebrazo 2.7091766 1.43518592 4.14078907 4.08319278 1.104704515
#> muñeca 1.4962208 0.89590495 1.78298568 1.10470452 0.871580820
precision <- round(100*solve(cor(bodyfat[,-1])))
round(100*cov2pcor(cov(bodyfat)))
#> densidad grasacorp edad peso estatura cuello pecho abdomen
#> densidad 100 -96 5 8 0 1 7 -14
#> grasacorp -96 100 8 4 -2 -3 6 4
#> edad 5 8 100 -19 -13 10 3 30
#> peso 8 4 -19 100 44 27 40 23
#> estatura 0 -2 -13 44 100 -3 -21 -6
#> cuello 1 -3 10 27 -3 100 3 10
#> pecho 7 6 3 40 -21 3 100 39
#> abdomen -14 4 30 23 -6 10 39 100
#> cadera 6 3 -7 52 -25 -18 -19 26
#> muslo -6 -3 -37 7 -20 12 -15 4
#> rodilla -1 0 25 25 9 -15 -9 -6
#> tobillo -10 -8 -10 19 -6 -9 -2 -12
#> biceps -9 -7 7 19 -5 9 9 -15
#> antebrazo -1 4 -18 3 -1 13 12 -13
#> muñeca 6 0 35 11 9 26 -2 0
#> cadera muslo rodilla tobillo biceps antebrazo muñeca
#> densidad 6 -6 -1 -10 -9 -1 6
#> grasacorp 3 -3 0 -8 -7 4 0
#> edad -7 -37 25 -10 7 -18 35
#> peso 52 7 25 19 19 3 11
#> estatura -25 -20 9 -6 -5 -1 9
#> cuello -18 12 -15 -9 9 13 26
#> pecho -19 -15 -9 -2 9 12 -2
#> abdomen 26 4 -6 -12 -15 -13 0
#> cadera 100 33 4 -4 -7 -8 0
#> muslo 33 100 27 -2 25 -1 -4
#> rodilla 4 27 100 17 -8 9 7
#> tobillo -4 -2 17 100 -5 -3 25
#> biceps -7 25 -8 -5 100 28 6
#> antebrazo -8 -1 9 -3 28 100 20
#> muñeca 0 -4 7 25 6 20 100
bodyfat.1 <- bodyfat[,c('grasacorp','abdomen','peso','estatura','biceps','antebrazo',
'rodilla','muñeca')]
summary(bodyfat.1)
#> grasacorp abdomen peso estatura
#> Min. : 0.00 Min. : 69.40 Min. :118.5 Min. :29.50
#> 1st Qu.:12.47 1st Qu.: 84.58 1st Qu.:159.0 1st Qu.:68.25
#> Median :19.20 Median : 90.95 Median :176.5 Median :70.00
#> Mean :19.15 Mean : 92.56 Mean :178.9 Mean :70.15
#> 3rd Qu.:25.30 3rd Qu.: 99.33 3rd Qu.:197.0 3rd Qu.:72.25
#> Max. :47.50 Max. :148.10 Max. :363.1 Max. :77.75
#> biceps antebrazo rodilla muñeca
#> Min. :24.80 Min. :21.00 Min. :33.00 Min. :15.80
#> 1st Qu.:30.20 1st Qu.:27.30 1st Qu.:36.98 1st Qu.:17.60
#> Median :32.05 Median :28.70 Median :38.50 Median :18.30
#> Mean :32.27 Mean :28.66 Mean :38.59 Mean :18.23
#> 3rd Qu.:34.33 3rd Qu.:30.00 3rd Qu.:39.92 3rd Qu.:18.80
#> Max. :45.00 Max. :34.90 Max. :49.10 Max. :21.40
bodyfat.1 <- subset(bodyfat.1, estatura > 30 & peso <300)
pairs(bodyfat.1)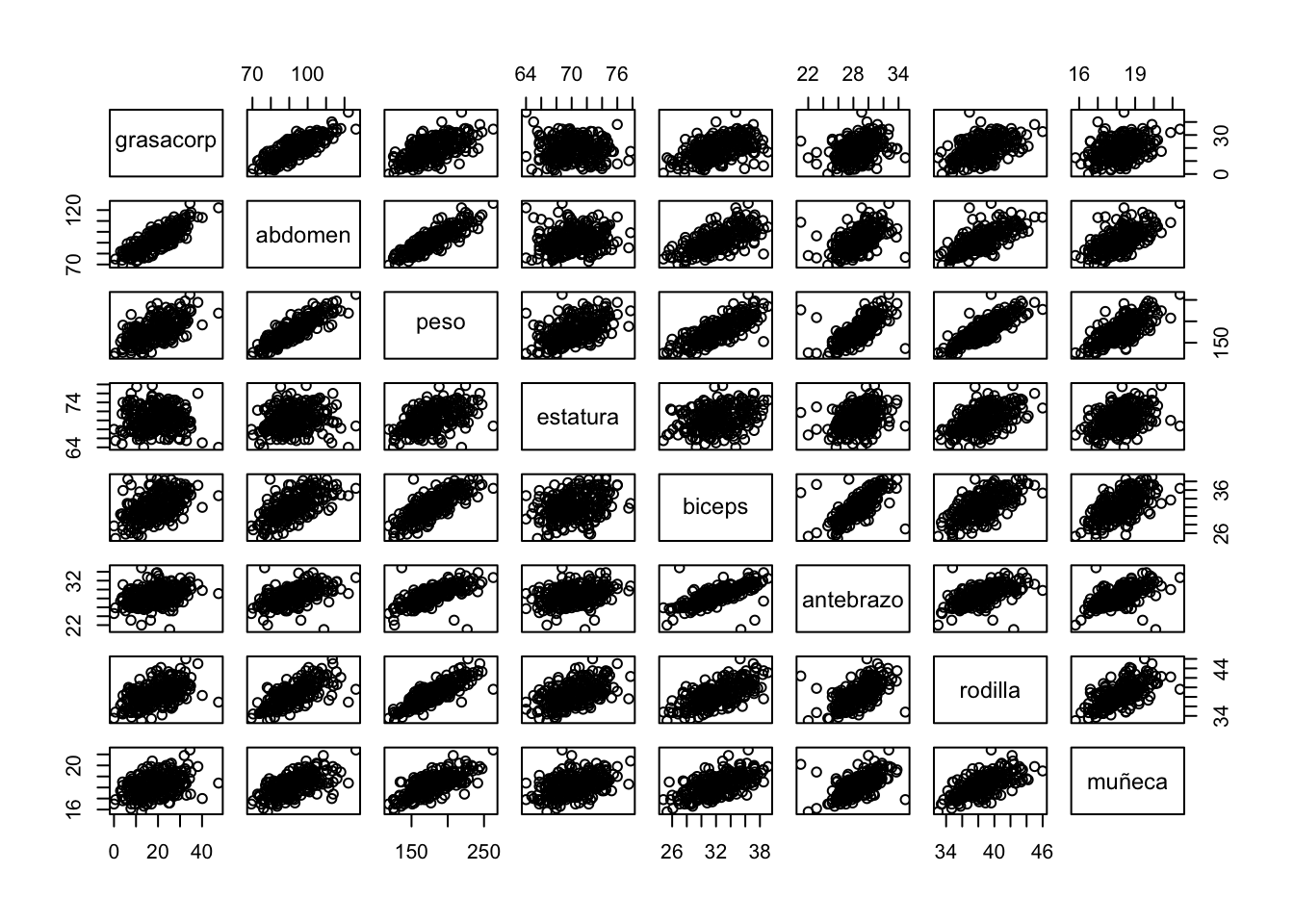
Usamos el criterio bic ajustando modelos hacia adelante obtenemos:
mod.1 <- cmod(~.^1, data=bodyfat.1)
plot(mod.2 <- forward(mod.1, k=log(nrow(bodyfat.1)), type='unrestricted'))
#> change.AIC -354.8385 Edge added: abdomen peso
#> change.AIC -304.1353 Edge added: peso rodilla
#> change.AIC -278.1341 Edge added: abdomen grasacorp
#> change.AIC -234.1223 Edge added: peso biceps
#> change.AIC -180.9975 Edge added: peso muñeca
#> change.AIC -163.5689 Edge added: biceps antebrazo
#> change.AIC -70.7975 Edge added: peso estatura
#> change.AIC -211.9549 Edge added: estatura grasacorp
#> change.AIC -83.0803 Edge added: abdomen estatura
#> change.AIC -46.2559 Edge added: muñeca antebrazo
#> change.AIC -26.0306 Edge added: muñeca grasacorp
#> change.AIC -11.4932 Edge added: peso antebrazo
#> change.AIC -9.9454 Edge added: estatura rodilla
#> change.AIC -8.7992 Edge added: biceps estatura
#> change.AIC -26.5494 Edge added: biceps abdomen
#> change.AIC -4.1848 Edge added: peso grasacorp
#> change.AIC -4.3748 Edge added: abdomen antebrazo
#> change.AIC -2.7400 Edge added: estatura antebrazo
#> change.AIC -0.4849 Edge added: abdomen muñeca
#> change.AIC -1.0522 Edge added: rodilla muñeca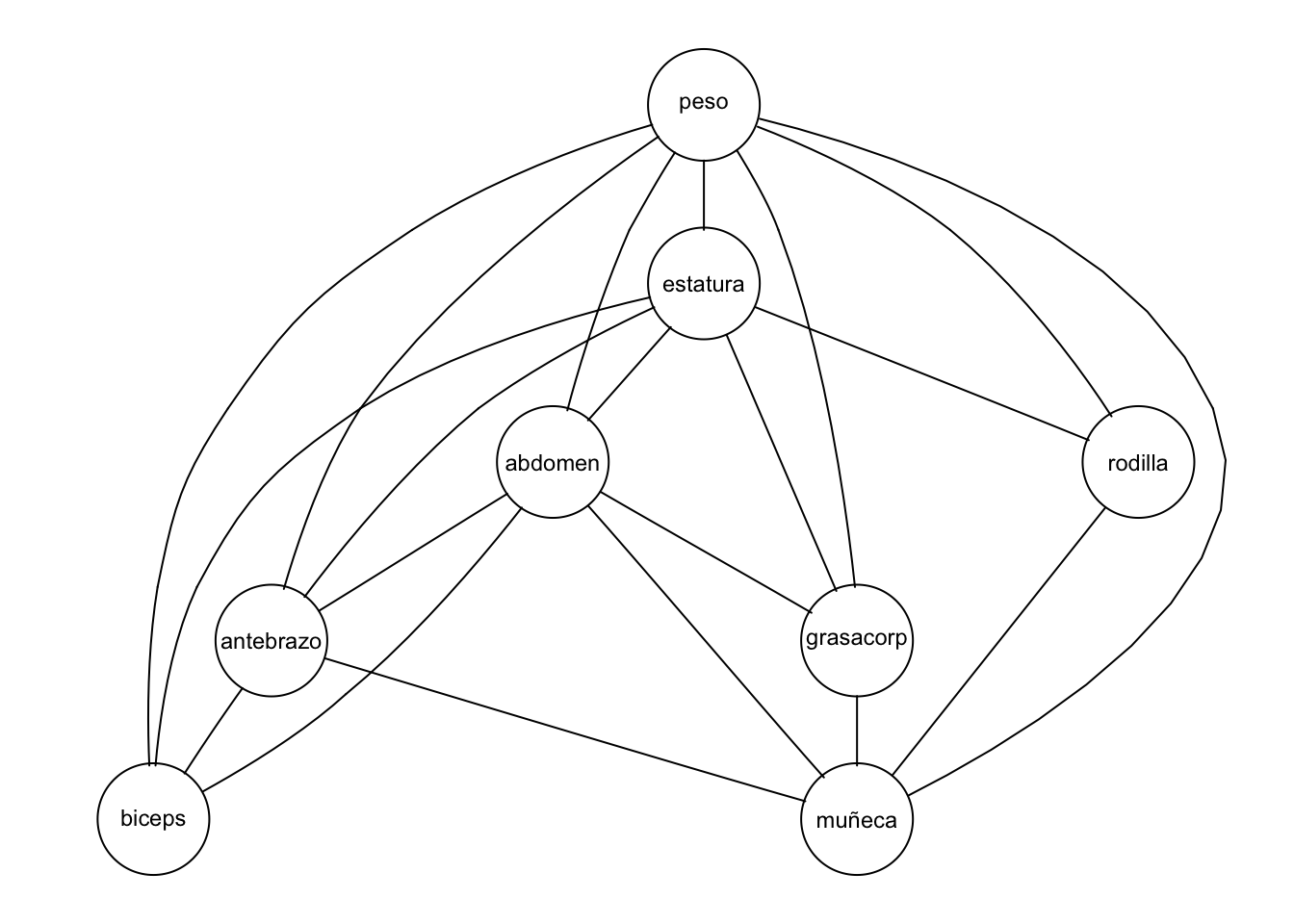
Podemos checar el ajuste del modelo verificando que la matriz ajustada de correlaciones es similar a la observada:
D <- mod.2$fitinfo$K
round(cor(bodyfat.1[,]),2)
#> grasacorp abdomen peso estatura biceps antebrazo rodilla muñeca
#> grasacorp 1.00 0.82 0.62 -0.03 0.48 0.36 0.49 0.34
#> abdomen 0.82 1.00 0.87 0.19 0.66 0.53 0.71 0.60
#> peso 0.62 0.87 1.00 0.51 0.79 0.68 0.84 0.73
#> estatura -0.03 0.19 0.51 1.00 0.32 0.32 0.51 0.40
#> biceps 0.48 0.66 0.79 0.32 1.00 0.70 0.65 0.61
#> antebrazo 0.36 0.53 0.68 0.32 0.70 1.00 0.58 0.60
#> rodilla 0.49 0.71 0.84 0.51 0.65 0.58 1.00 0.66
#> muñeca 0.34 0.60 0.73 0.40 0.61 0.60 0.66 1.00
round(cov2cor(solve(D)),2)
#> grasacorp abdomen peso estatura biceps antebrazo rodilla muñeca
#> grasacorp 1.00 0.82 0.62 -0.03 0.45 0.33 0.47 0.34
#> abdomen 0.82 1.00 0.87 0.19 0.66 0.53 0.71 0.60
#> peso 0.62 0.87 1.00 0.51 0.79 0.68 0.84 0.73
#> estatura -0.03 0.19 0.51 1.00 0.32 0.32 0.51 0.40
#> biceps 0.45 0.66 0.79 0.32 1.00 0.70 0.66 0.60
#> antebrazo 0.33 0.53 0.68 0.32 0.70 1.00 0.58 0.60
#> rodilla 0.47 0.71 0.84 0.51 0.66 0.58 1.00 0.66
#> muñeca 0.34 0.60 0.73 0.40 0.60 0.60 0.66 1.00Y vemos que en en efecto estas dos matrices son muy similares.
En muchos casos, estos modelos presentan algunas correlaciones débiles que, aunque nos pueden interesar, pueden hacer difícil entender los rasgos importantes de nuestros datos. Vale la pena examinar ajustes penalizando por complejidad más fuertemente, y viendo qué tanto cambia la calidad del ajuste. Por ejemplo, si incrementamos la penalización (el bic da una penalización de 5):
plot(mod.3 <- forward(mod.1, k=20, type='unrestricted'))
#> change.AIC -340.3599 Edge added: abdomen peso
#> change.AIC -289.6568 Edge added: peso rodilla
#> change.AIC -263.6555 Edge added: abdomen grasacorp
#> change.AIC -219.6437 Edge added: peso biceps
#> change.AIC -166.5189 Edge added: peso muñeca
#> change.AIC -149.0904 Edge added: biceps antebrazo
#> change.AIC -56.3189 Edge added: peso estatura
#> change.AIC -197.4764 Edge added: estatura grasacorp
#> change.AIC -68.6018 Edge added: abdomen estatura
#> change.AIC -31.7774 Edge added: muñeca antebrazo
#> change.AIC -11.5520 Edge added: muñeca grasacorp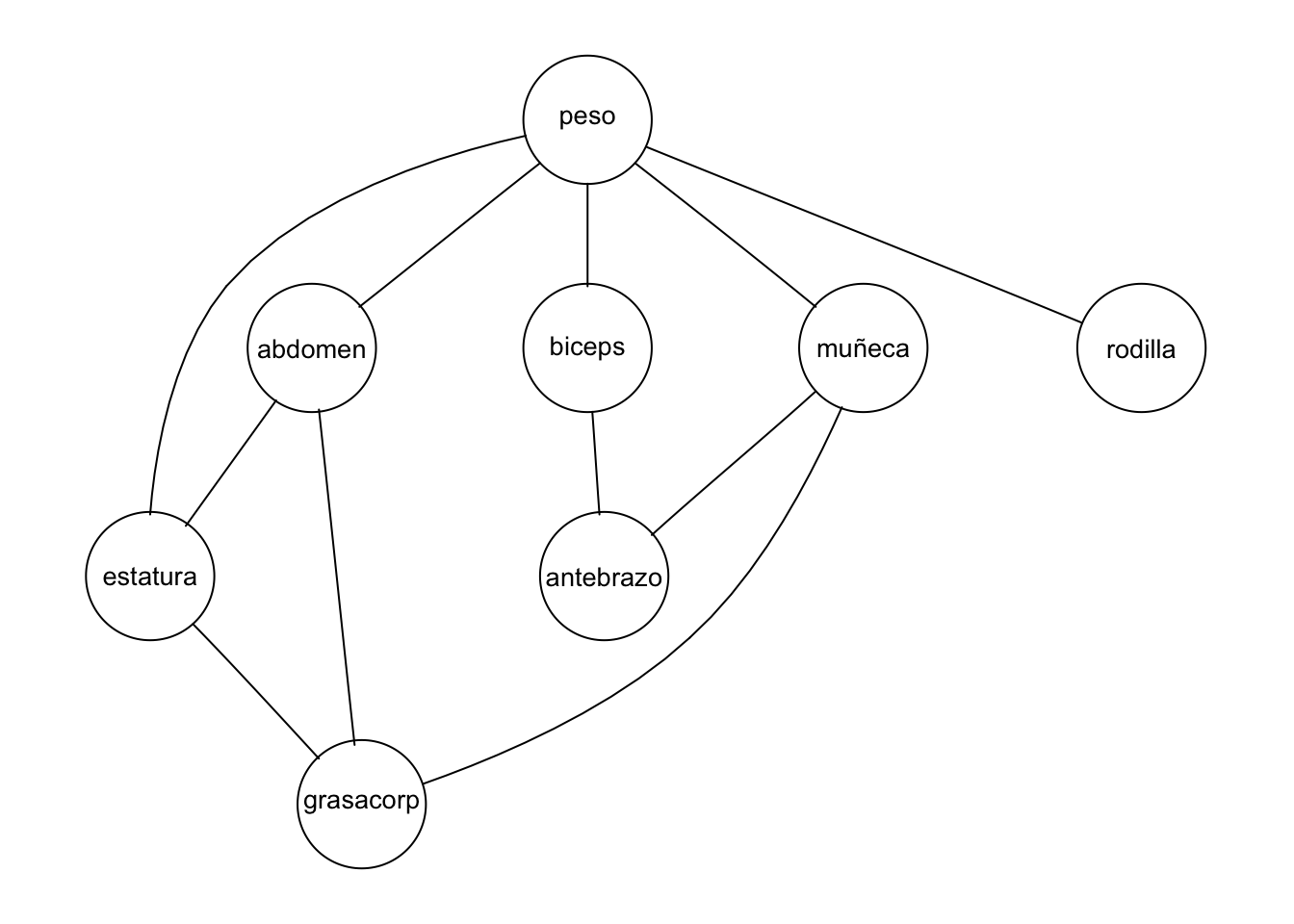
D <- mod.2$fitinfo$K
parciales.D <- -(t(D*(1/sqrt(diag(D))))*(1/sqrt(diag(D))))
graf.1 <- ugList(mod.3$glist)
nombres <- sapply(edgeList(graf.1), function(x){
nombre <- paste0('',paste(c(x[1],x[2]), collapse="~"),'')
nombre
})
peso <- sapply(edgeList(graf.1), function(x){
peso <- as.character(round(parciales.D[x[1],x[2]],2))
})
etiquetas <- peso
names(etiquetas) <- nombres
plot(graf.1, edgeAttrs=list(label=etiquetas))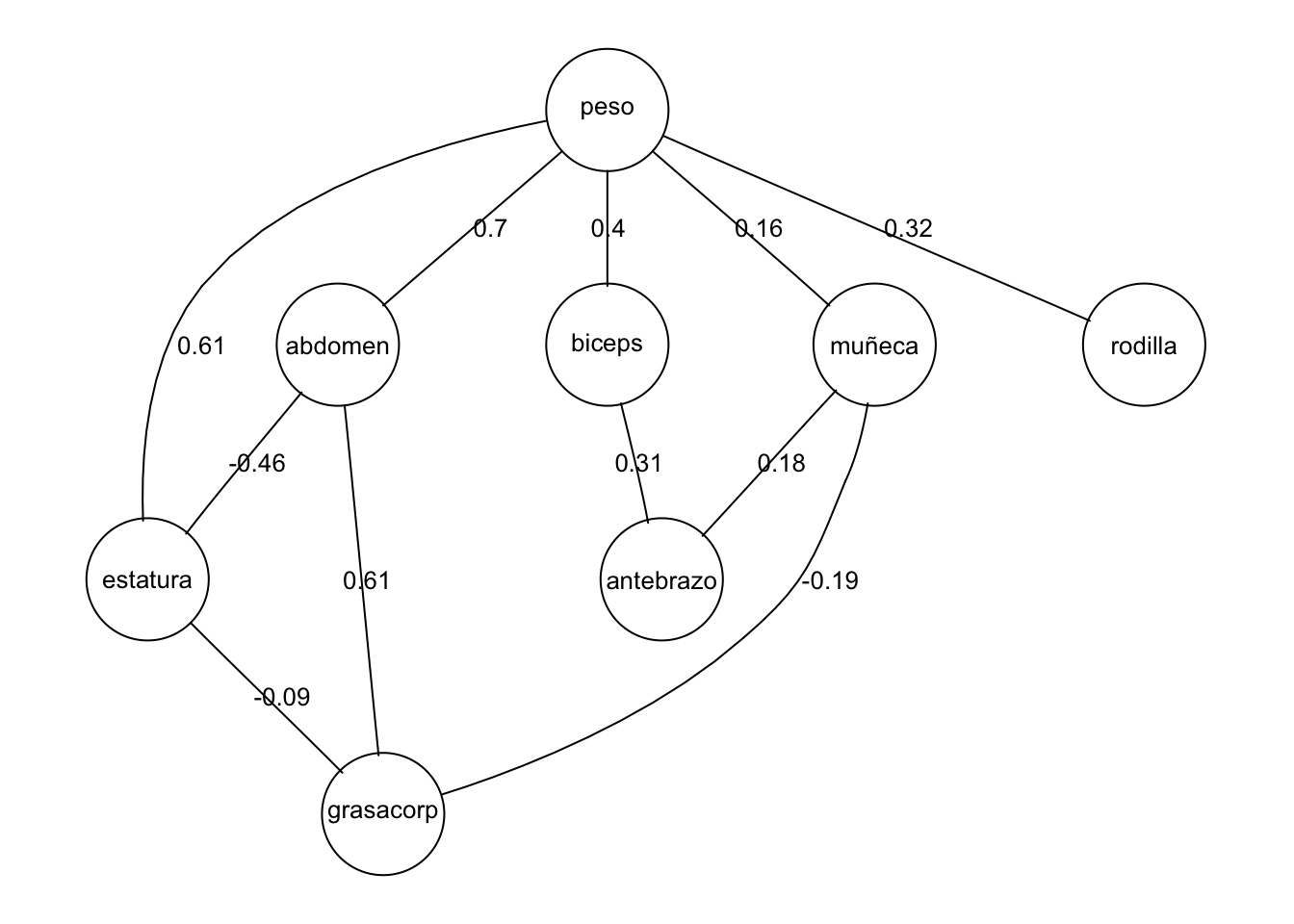
Este modelo establece, por ejemplo, que dado peso, biceps y estatura son independientes:
library(Hmisc)
library(ggplot2)
bodyfat.2 <- bodyfat.1
bodyfat.2$grupo.peso <- cut2(bodyfat.2$peso, g=5)
ggplot(bodyfat.2, aes(x=biceps, y=estatura)) +
geom_point() +
facet_wrap(~grupo.peso, nrow = 1) +
geom_smooth()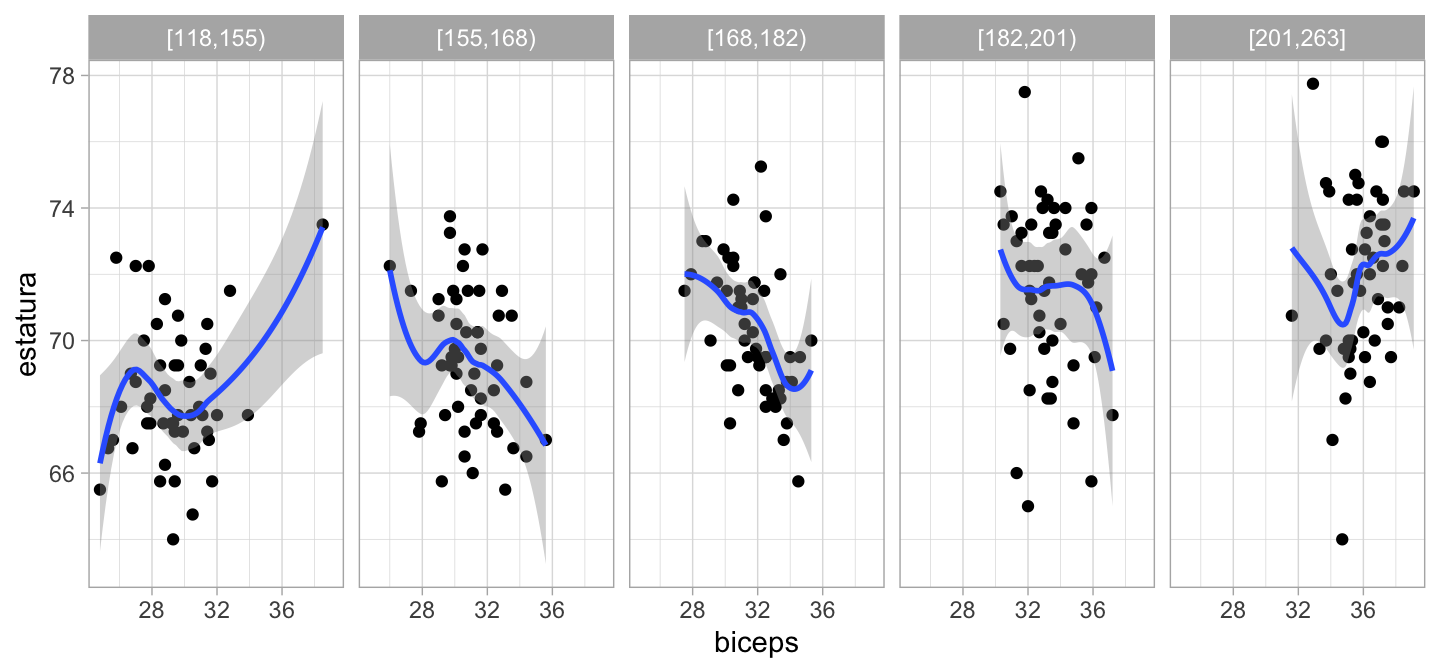
Sin condicionar observamos,
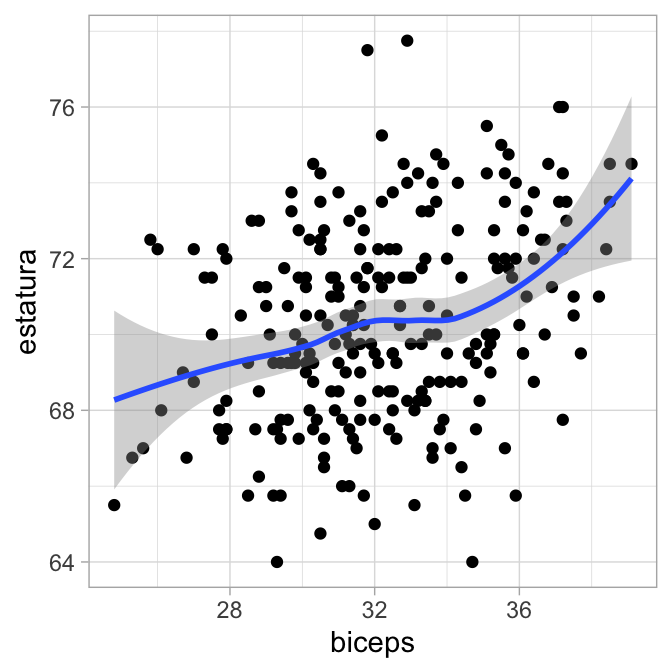
Comparando las matrices de correlaciones.
D <- mod.3$fitinfo$K
round(cor(bodyfat.1[,]),2)
#> grasacorp abdomen peso estatura biceps antebrazo rodilla muñeca
#> grasacorp 1.00 0.82 0.62 -0.03 0.48 0.36 0.49 0.34
#> abdomen 0.82 1.00 0.87 0.19 0.66 0.53 0.71 0.60
#> peso 0.62 0.87 1.00 0.51 0.79 0.68 0.84 0.73
#> estatura -0.03 0.19 0.51 1.00 0.32 0.32 0.51 0.40
#> biceps 0.48 0.66 0.79 0.32 1.00 0.70 0.65 0.61
#> antebrazo 0.36 0.53 0.68 0.32 0.70 1.00 0.58 0.60
#> rodilla 0.49 0.71 0.84 0.51 0.65 0.58 1.00 0.66
#> muñeca 0.34 0.60 0.73 0.40 0.61 0.60 0.66 1.00
round(cov2cor(solve(D)),2)
#> grasacorp abdomen peso estatura biceps antebrazo rodilla muñeca
#> grasacorp 1.00 0.82 0.64 -0.03 0.49 0.35 0.54 0.34
#> abdomen 0.82 1.00 0.87 0.19 0.68 0.52 0.74 0.58
#> peso 0.64 0.87 1.00 0.51 0.79 0.61 0.84 0.73
#> estatura -0.03 0.19 0.51 1.00 0.41 0.34 0.43 0.45
#> biceps 0.49 0.68 0.79 0.41 1.00 0.70 0.66 0.62
#> antebrazo 0.35 0.52 0.61 0.34 0.70 1.00 0.52 0.60
#> rodilla 0.54 0.74 0.84 0.43 0.66 0.52 1.00 0.61
#> muñeca 0.34 0.58 0.73 0.45 0.62 0.60 0.61 1.00Donde vemos que este modelo más simple recupera razonablemente bien la estructura de covarianza.
 Utiliza los datos carcass para
crear un modelo gráfico Gaussiano. ¿Qué relaciones de independencia condicional
lees en la gráfica?
Utiliza los datos carcass para
crear un modelo gráfico Gaussiano. ¿Qué relaciones de independencia condicional
lees en la gráfica?
4.3.1 Supuesto de normalidad multivariada
Finalizamos recordando el inicio de la sección: el supuesto de normalidad multivariada es en general difícil de verificar. Generalmente, se considera que la pregunta interesante es si los datos son suficientemente cercanos a normalidad para aplicar un procedimiento dado. Existen diagnósticos, pero aquí consideramos que estos modelos gaussianos, típicamente, pueden utilizarse más como procedimientos exploratorios.