9.8 JAGS
JAGS (Just Another Gibbs Sampler), WinBUGS y
OpenBUGS son programas que
implementan métodos MCMC para generar simulaciones de distribuciones
posteriores. Los paquetes rjags y R2jags permiten ajustar modelos en JAGS
desde R. Es muy fácil utilizar estos programas pues uno simplemente debe
especificar las distribuciones iniciales, la verosimilitud y los datos
observados.
Especificación del modelo
Repitamos el caso del sesgo de la modela usando JAGS. Vale la pena realizar un diagrama.

El diagrama captura las dependencias entre los datos y los parámetros y veremos que puede facilitar la implementación en JAGS pues cada flecha en el diagrama corresponde a una línea de código en la especificación del modelo.
el ciclo for indica que cada dato observado proviene de una distribución Bernoulli con parámetro . Afuera del ciclo escribimos las distribución inicial, .
Inicializar cadenas
El modelo ya esta especificado, pero aún debemos indicar los valores de las variables en el modelo, para esto definimos los valores en R y después los mandamos a JAGS.
Falta especificar el valor inicial de , JAGS tiene una manera de hacerlo automaticamente, pero muchas veces vale la pena tener control de los valores iniciales. En ocasiones la eficiencia del proceso puede incrementar si seleccionamos valores iniciales razonables. Kruschke sugiere utilizar como puntos iniciales los estimadores de máxima verosimilitud, esto es porque usualmente la distribución posterior no esta muy lejana de la función de verosimilitud. En este caso el estimador de máxima verosimilitud para es .
Esta manera de especificar los valores iniciales no siempre se recomienda pues cuando queremos evaluar la convergencia de la cadena muchas veces se sugiere correr varias cadenas con puntos iniciales muy dispersos a lo largo del espacio de parámetros, de tal manera que cuando las cadenas convergen se pueda determinar que la etapa de calentamiento a terminado. Un punto medio es iniciar las cadenas en un punto aleatorio cercano al estimador de máxima verosimilitud.
Generar las cadenas
Ahora llamamos a JAGS y generamos las cadenas. Para esto usaremos el paquete
R2jags, otro paquete para llamar JAGS desde R es rjags.
library(R2jags)
#> Loading required package: rjags
#> Linked to JAGS 4.2.0
#> Loaded modules: basemod,bugs
#>
#> Attaching package: 'R2jags'
#> The following object is masked from 'package:coda':
#>
#> traceplot
cat(modelo_bb.bugs, file = 'codigo_jags/modelo_bb.bugs')
jags_fit <- jags(
model.file = "codigo_jags/modelo_bb.bugs", # modelo de JAGS
inits = init_theta, # valores iniciales
data = list(x = x, N = N), # lista con los datos
parameters.to.save = c("theta"), # parámetros por guardar
n.chains = 1, # número de cadenas
n.iter = 1000, # número de pasos
n.burnin = 500 # calentamiento de la cadena
)
#> module glm loaded
#> Compiling model graph
#> Resolving undeclared variables
#> Allocating nodes
#> Graph information:
#> Observed stochastic nodes: 14
#> Unobserved stochastic nodes: 1
#> Total graph size: 18
#>
#> Initializing model
# plot(jags_fit)Podemos ver un resumen del ajuste:
head(jags_fit$BUGSoutput$summary)
#> mean sd 2.5% 25% 50% 75%
#> deviance 15.4603157 1.4002044 14.549411 14.6547197 14.9439815 15.6903684
#> theta 0.7461137 0.1033549 0.522712 0.6869913 0.7508565 0.8232681
#> 97.5%
#> deviance 19.1383724
#> theta 0.9284436Y graficar la cadena:

Ejemplo normal
Recordemos el ejemplo normal con media y varianza desconocidas. ¿Cuál es el modelo gráfico asociado?
N <- 50 # Observamos 20 realizaciones
set.seed(122)
x <- rnorm(N, 2, 2)
modelo_normal.bugs <-
'
model{
for(i in 1:N){
x[i] ~ dnorm(mu, nu)
}
# iniciales
nu ~ dgamma(3, 3)
sigma2 <- 1 / nu
mu ~ dnorm(1.5, 1 / 16)
}
'el ciclo for indica que cada dato observado proviene de una distribución
Normal con media y varinza (precisión ). Afuera del ciclo
escribimos las distribuciones iniciales, , esto es
y se distribuye Normal con media y
varianza .
El modelo ya esta especificado, pero aun falta indicar los valores de las variables en el modelo, para esto definimos los valores en R y después los mandamos a JAGS.
cat(modelo_normal.bugs, file = 'codigo_jags/modelo_normal.bugs')
# valores iniciales para los parámetros, si no se especifican la función jags
# generará valores iniciales
jags_inits <- function(){
list(mu = rnorm(1, mean(x), 5), nu = 1 / runif(1, 2, 4))
}
jags_fit <- jags(
model.file = "codigo_jags/modelo_normal.bugs", # modelo de JAGS
inits = jags_inits, # valores iniciales
data = list(x = x, N = N), # lista con los datos
parameters.to.save = c("mu", "sigma2"), # parámetros por guardar
n.chains = 1, # número de cadenas
n.iter = 10000, # número de pasos
n.burnin = 1000, # calentamiento de la cadena
n.thin = 1
)
#> Compiling model graph
#> Resolving undeclared variables
#> Allocating nodes
#> Graph information:
#> Observed stochastic nodes: 50
#> Unobserved stochastic nodes: 2
#> Total graph size: 62
#>
#> Initializing model
jags_fit
#> Inference for Bugs model at "codigo_jags/modelo_normal.bugs", fit using jags,
#> 1 chains, each with 10000 iterations (first 1000 discarded)
#> n.sims = 9000 iterations saved
#> mu.vect sd.vect 2.5% 25% 50% 75% 97.5%
#> mu 1.913 0.313 1.308 1.704 1.912 2.119 2.531
#> sigma2 4.751 1.449 3.247 4.073 4.623 5.277 6.913
#> deviance 223.496 2.388 221.460 222.003 222.825 224.272 229.279
#>
#> DIC info (using the rule, pD = var(deviance)/2)
#> pD = 2.9 and DIC = 226.3
#> DIC is an estimate of expected predictive error (lower deviance is better).
# podemos ver las cadenas
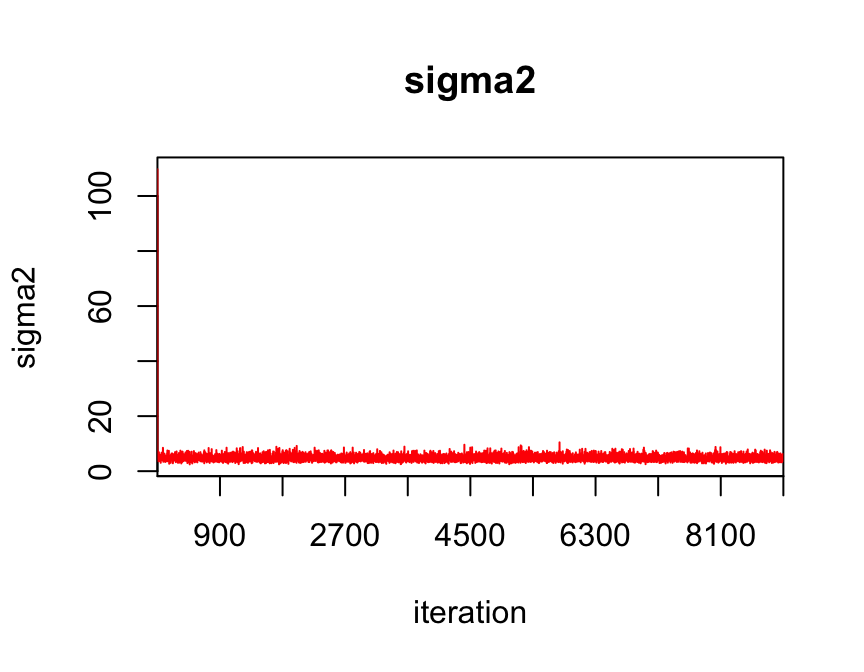
traceplot(jags_fit, varname = c("mu", "sigma2"))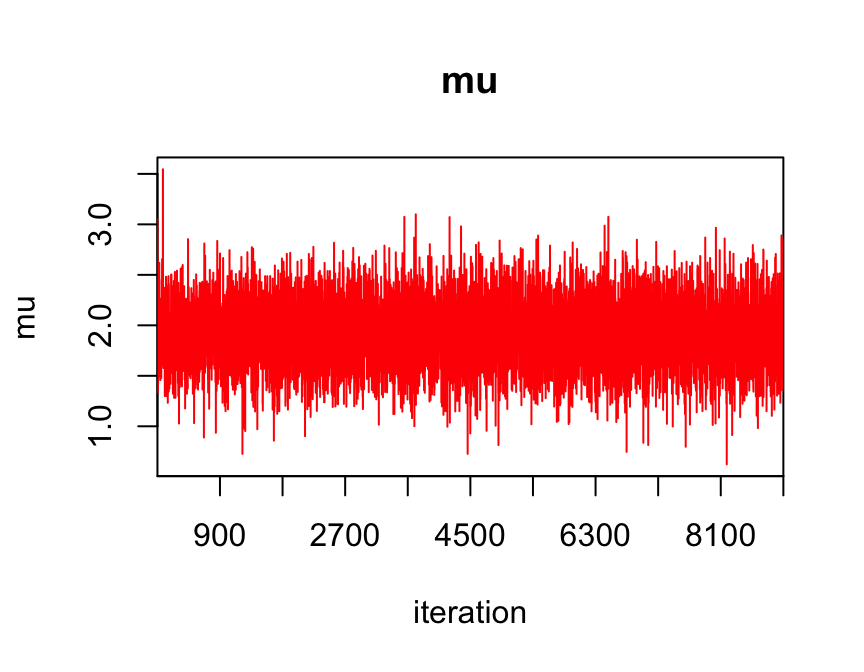
 Realiza un histograma de la distribución
predictiva. Construye un intervalo de de probabilidad para la predicción.
Pista: utiliza
Realiza un histograma de la distribución
predictiva. Construye un intervalo de de probabilidad para la predicción.
Pista: utiliza jags_fit$BUGSoutput$sims.matrix.