1.1 Patrones complejos de dependencia
Cuando consideramos dos variables aleatorias, tenemos herramientas simples para describir dependencia:
Por ejemplo, para dos variables numéricas, podemos usar correlaciones. En este ejemplo, rendimiento de coches y cilindros están negativamente correlacionadas:
library(ggplot2)
cor(mpg[,c('cyl','cty')])
#> cyl cty
#> cyl 1.0000000 -0.8057714
#> cty -0.8057714 1.0000000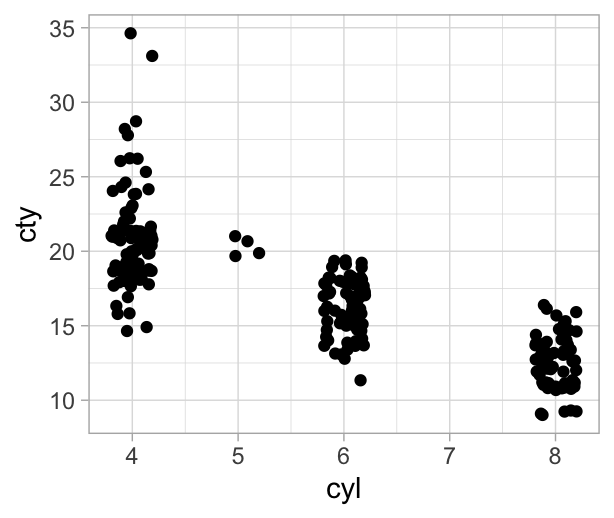
Para variables categóricas podemos usar tablas para entender cómo está relacionada la transmisión y el tipo de coche,
table(mpg$class, mpg$drv)
#>
#> 4 f r
#> 2seater 0 0 5
#> compact 12 35 0
#> midsize 3 38 0
#> minivan 0 11 0
#> pickup 33 0 0
#> subcompact 4 22 9
#> suv 51 0 11podemos calcular las distribuciones condicionales empíricas dado el tipo de coche:
round(100 * prop.table(table(mpg$class, mpg$drv), margin = 1))
#>
#> 4 f r
#> 2seater 0 0 100
#> compact 26 74 0
#> midsize 7 93 0
#> minivan 0 100 0
#> pickup 100 0 0
#> subcompact 11 63 26
#> suv 82 0 18O podemos sacar las condicionales empíricas dado el tipo de transmición:
round(100 * prop.table(table(mpg$class, mpg$drv), margin = 2))
#>
#> 4 f r
#> 2seater 0 0 20
#> compact 12 33 0
#> midsize 3 36 0
#> minivan 0 10 0
#> pickup 32 0 0
#> subcompact 4 21 36
#> suv 50 0 44Sin embargo, cuando tenemos más de dos variables, los patrones de asociación tienen más riqueza. Como ejemplo, pensemos en un problema ficticio, con tres variables binarias: si el jardín está mojado o no, si llovió o no llovió, y si el jardín fue o no regado. Vemos que regar el jardín no está relacionado con que llueva o no:
load('data/lluvia.Rdata')
table(lluvia$lluvia, lluvia$regar)
#>
#> 0 1
#> 0 394 76
#> 1 107 23
prop.table(table(lluvia$lluvia, lluvia$regar), margin = 1)
#>
#> 0 1
#> 0 0.8382979 0.1617021
#> 1 0.8230769 0.1769231Pero si condiconamos a que el pasto está mojado, entonces lluvia y regar están inversamente correlacionados, un ejemplo de porque ocurre es que si el suelo está mojado y no hay lluvia entonces se regó el jardín,
table(lluvia$lluvia, lluvia$regar, lluvia$mojado)
#> , , = FALSE
#>
#>
#> 0 1
#> 0 394 0
#> 1 0 0
#>
#> , , = TRUE
#>
#>
#> 0 1
#> 0 0 76
#> 1 107 23
prop.table(table(lluvia$lluvia, lluvia$regar, lluvia$mojado), margin = c(1, 3))
#> , , = FALSE
#>
#>
#> 0 1
#> 0 1.0000000 0.0000000
#> 1
#>
#> , , = TRUE
#>
#>
#> 0 1
#> 0 0.0000000 1.0000000
#> 1 0.8230769 0.1769231Otro ejemplo de dependencia, tomado de Gelman, es un análisis de votantes en Estados Unidos, votantes más ricos tienden a votar más por el partido republicano. Sin embargo, estados más ricos tienden a votar más por demócratas. La relación de dependencia se ve en distintas direcciones dependiendo del nivel que lo veamos (estado o individuo):
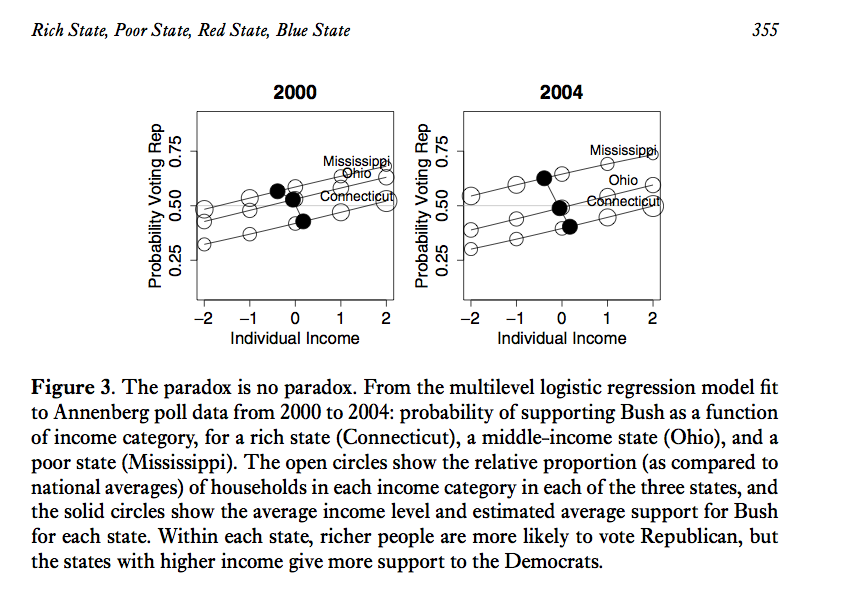
1.1.1 Modelos gráficos
Un modelo gráfico es una red de variables aleatorias donde:
Nodos representan variables aleatorias.
Arcos (dirigidos o no) representan dependencia
Los dos esquemas generales para representar dependencias/independiencias (condicionales) de forma gráfica son los modelos dirigidos (redes bayesianas) y no dirigidos (redes markovianas).
Veamos un ejemplo de un modelo gráfico no dirigido.
Consideramos las calificaciones de 88 alumnos (Mardia 1979) en cinco áreas: vectores (VECT), mecánica (MECH), álgebra (ALG), análisis (ANL) y estadística (STAT)). Podemos representar la estrucutra de covarianza con una gráfica como la siguiente:
library(bnlearn)
#>
#> Attaching package: 'bnlearn'
#> The following object is masked from 'package:stats':
#>
#> sigma
data(marks)
head(marks)
#> MECH VECT ALG ANL STAT
#> 1 77 82 67 67 81
#> 2 63 78 80 70 81
#> 3 75 73 71 66 81
#> 4 55 72 63 70 68
#> 5 63 63 65 70 63
#> 6 53 61 72 64 73
library(ggplot2)
library(Hmisc)
#> Loading required package: lattice
#> Loading required package: survival
#> Loading required package: Formula
#>
#> Attaching package: 'Hmisc'
#> The following object is masked from 'package:bnlearn':
#>
#> impute
#> The following objects are masked from 'package:dplyr':
#>
#> src, summarize
#> The following objects are masked from 'package:base':
#>
#> format.pval, units
marks.graph <- gs(marks)
graphviz.plot(marks.graph)
#> Loading required namespace: Rgraphviz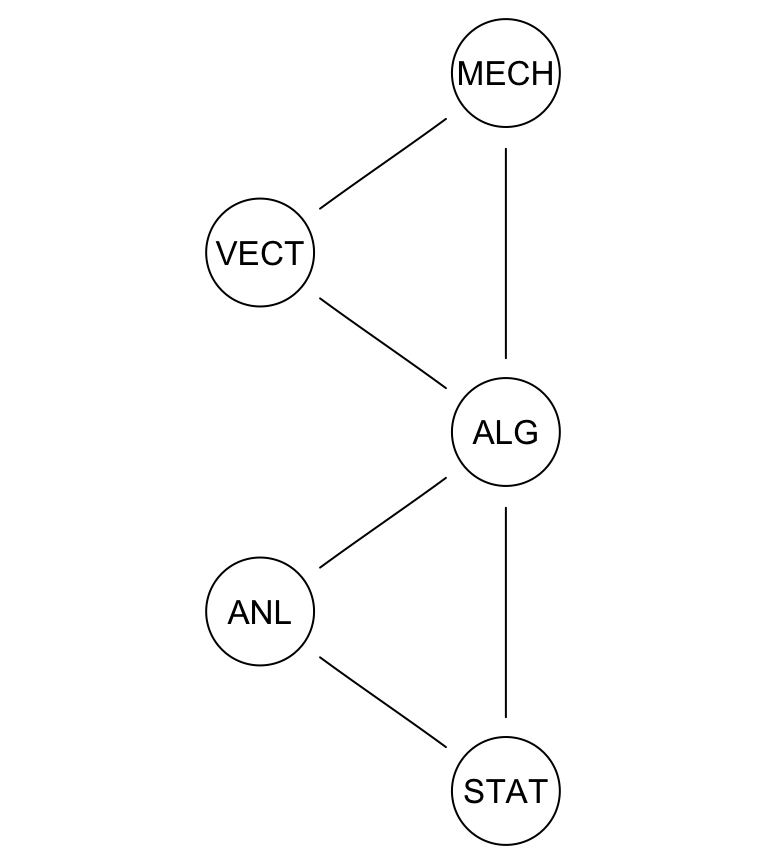
Veremos que este gráfico establece correlaciones entre álgebra, análisis y estadística, así como entre vectores, mecánica y álgebra. Esto implica, por ejemplo, mecánica está correlacionada con estadística:
ggplot(marks, aes(x = STAT, y = VECT)) +
geom_point() +
geom_smooth(span=1, method='loess', degree=1)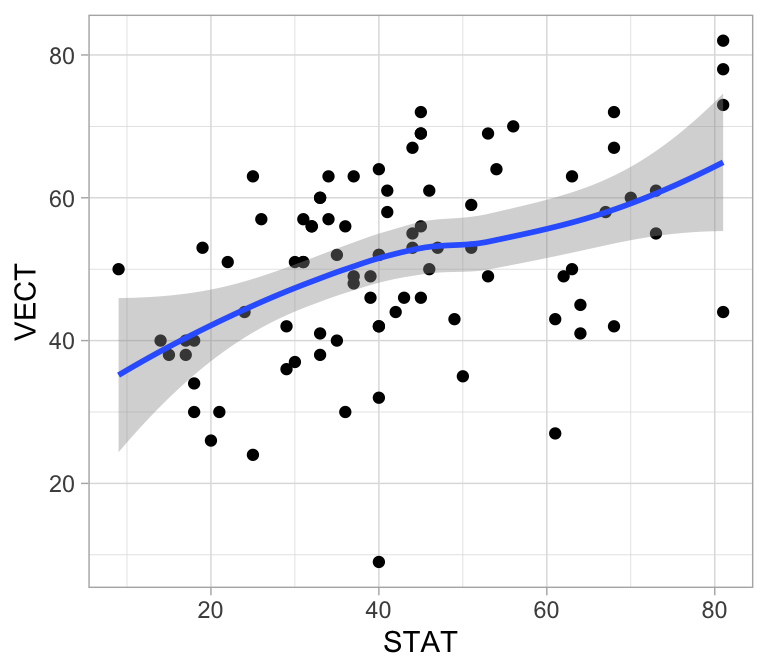
Pero también sugiere que dada la calificación de álgebra, estadística y vectores no están correlacionados:
marks$ALG_grupos <- cut2(marks$ALG, g = 4)
ggplot(marks, aes(x = STAT, y=VECT)) + facet_wrap(~ALG_grupos) + geom_point() +
geom_smooth(span=2, method='loess', degree=1)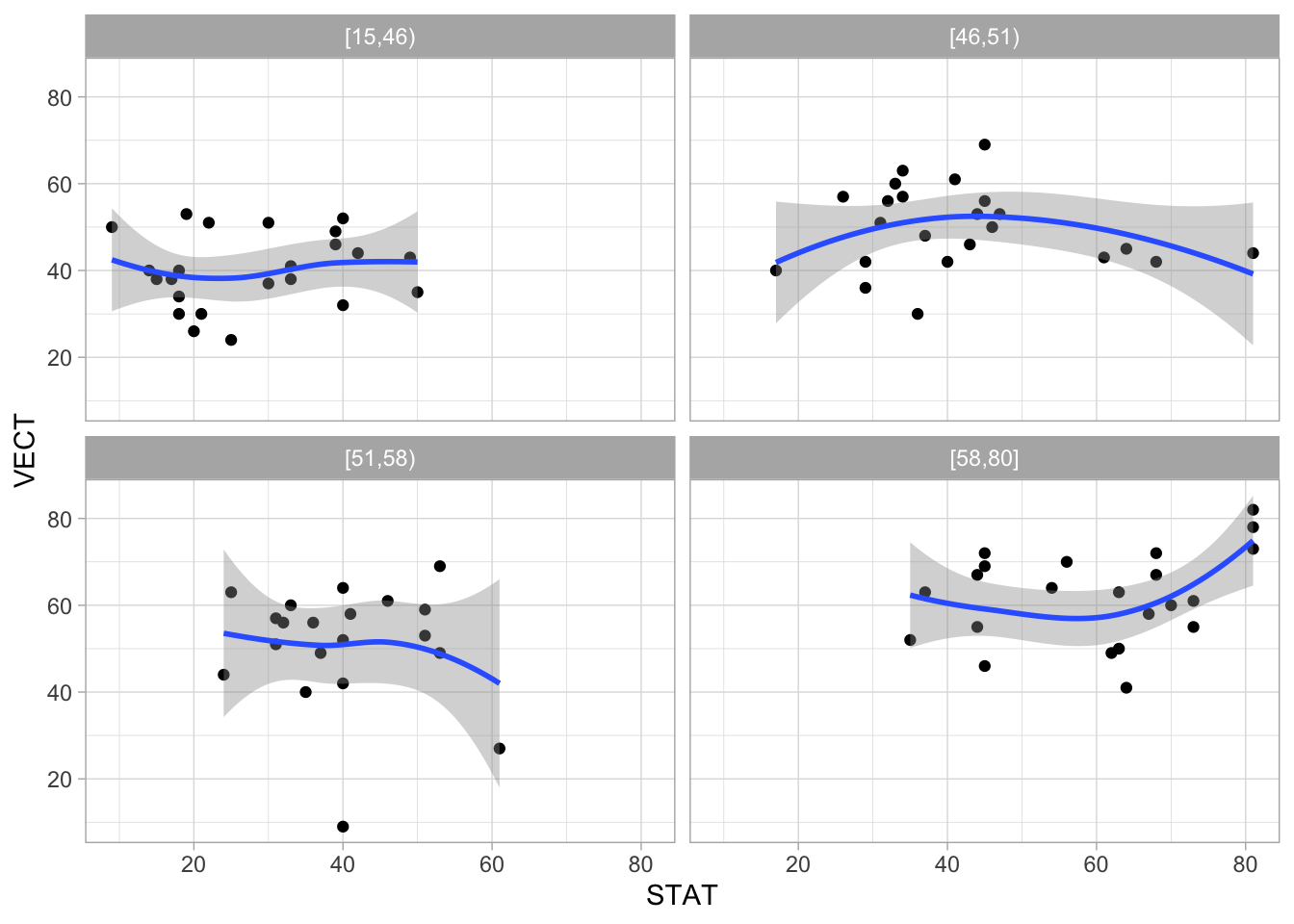
Lo cual no sucede por ejemplo, si estudiamos la asociación entre STAT y ANL condicionando a ALG:
ggplot(marks, aes(x=STAT, y=ANL)) + facet_wrap(~ALG_grupos) + geom_point() +
geom_smooth(span=2, method='loess', degree=1)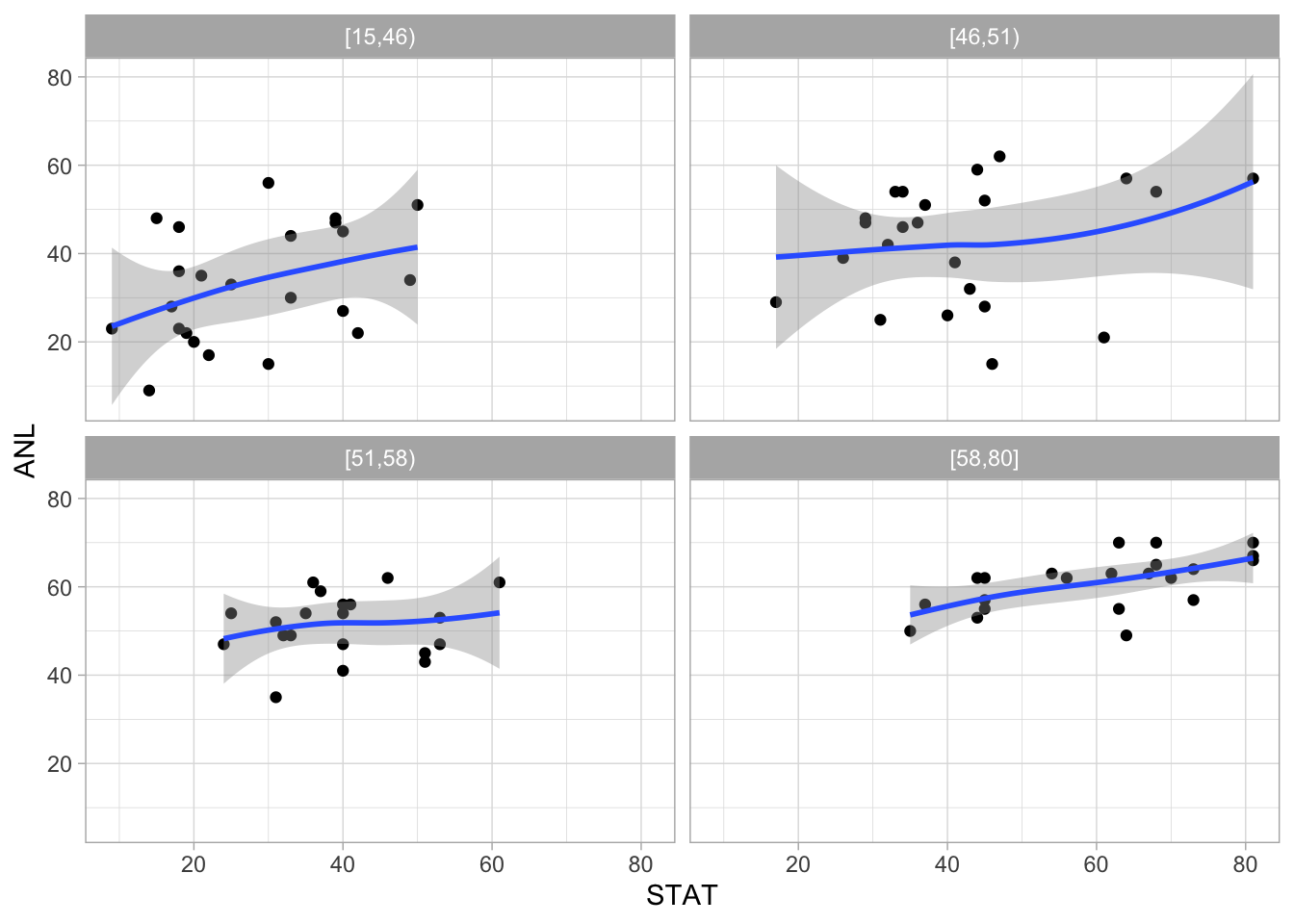
En la red que representa la estructura de dependencia de estos datos, el hecho de que ALG separa a VECT de STAT se interpreta como sigue: si hacemos una regresión de STAT en función de VECT, controlando por ALG, el coeficiente de VECT es 0.
Del modelo gráfico obtenemos varias simplificaciones (Whittaker):
Podemos entender la estructura de estos datos analizando dos grupos de tres variables cada uno, en lugar de intentar un análisis conjunto de las 5 variables.
Estamos en una mejor posición para modelar este problema: en un principio, estábamos en el punto de “todo se relaciona con todo”, y esto implica un modelo muy grande y complejo. Modelos tan grandes muchas veces son imposibles de tratar con cualquier conjunto de datos de tamaño usual. Las independiencias condicionales que acabamos de establecer simplifican considerablemente el tipo de modelos que debemos considerar.
Si quisiéramos predecir estadística (EST), por ejemplo, basta con usar álgebra y análisis. Esto puede permitirnos construir mejores modelos y más fáciles de entender.
Descubrimos que en un sentido al examen de álgebra es el más importante, pues podría fundamentar todas las demás. Por otra parte, también aprendimos que hay potencialmente dos habilidades adicionales al álgebra que están asociadas a VECT y MECH por un lado, y a STAT y ANL por otro.
Como ejemplo de modelos dirigidos veremos una red de seguros de auto.
En este ejemplo nos interesa entender los patrones de dependencia entre variables como edad, calidad de conductor y tipo de accidente:
library(bnlearn)
head(insurance)
#> GoodStudent Age SocioEcon RiskAversion VehicleYear ThisCarDam
#> 1 False Adult Prole Adventurous Older Moderate
#> 2 False Senior Prole Cautious Current None
#> 3 False Senior UpperMiddle Psychopath Current None
#> 4 False Adolescent Middle Normal Older None
#> 5 False Adolescent Prole Normal Older Moderate
#> 6 False Adult UpperMiddle Normal Current Moderate
#> RuggedAuto Accident MakeModel DrivQuality Mileage Antilock
#> 1 EggShell Mild Economy Poor TwentyThou False
#> 2 Football None Economy Normal TwentyThou False
#> 3 Football None FamilySedan Excellent Domino True
#> 4 EggShell None Economy Normal FiftyThou False
#> 5 Football Moderate Economy Poor FiftyThou False
#> 6 EggShell Moderate SportsCar Poor FiftyThou True
#> DrivingSkill SeniorTrain ThisCarCost Theft CarValue HomeBase AntiTheft
#> 1 SubStandard False TenThou False FiveThou City False
#> 2 Normal True Thousand False TenThou City True
#> 3 Normal False Thousand False TwentyThou City False
#> 4 Normal False Thousand False FiveThou Suburb False
#> 5 SubStandard False TenThou False FiveThou City False
#> 6 SubStandard False HundredThou False TwentyThou Suburb True
#> PropCost OtherCarCost OtherCar MedCost Cushioning Airbag ILiCost
#> 1 TenThou Thousand True Thousand Poor False Thousand
#> 2 Thousand Thousand True Thousand Good True Thousand
#> 3 Thousand Thousand False Thousand Good True Thousand
#> 4 Thousand Thousand True Thousand Fair False Thousand
#> 5 TenThou Thousand False Thousand Fair False Thousand
#> 6 HundredThou HundredThou True TenThou Poor True Thousand
#> DrivHist
#> 1 Many
#> 2 Zero
#> 3 One
#> 4 Zero
#> 5 Many
#> 6 Many
insurance_dat <- insurance[, c('Age', 'GoodStudent', 'SocioEcon', 'RiskAversion',
'Accident','DrivQuality')]
blacklist <- data.frame(from=c('DrivQuality','Accident'), to=c('Age','DrivQuality'))Utilizamos una red bayesiana:
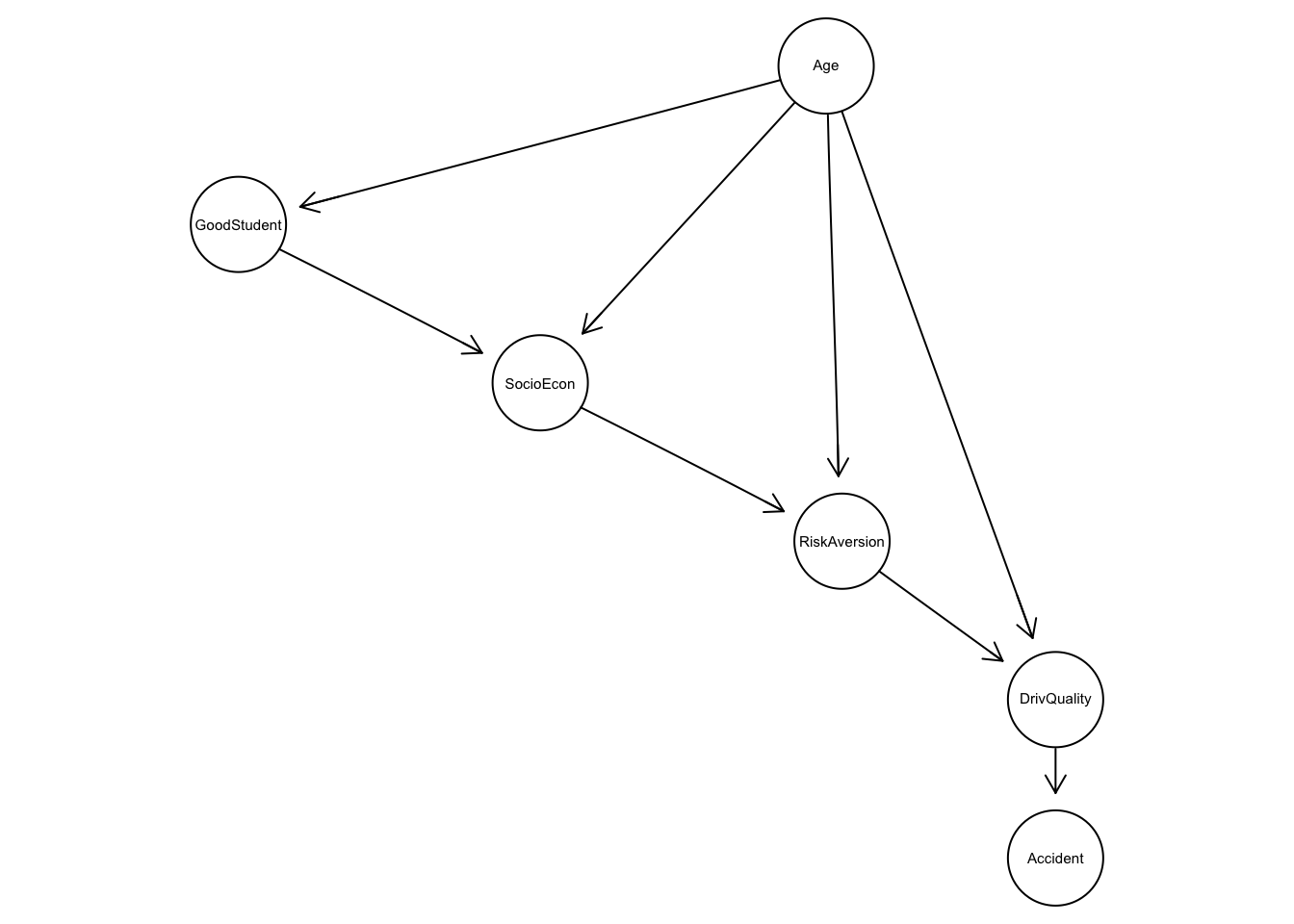
insurance.fit <- bn.fit(insurance_gm, data = insurance_dat, method = 'bayes',
iss = 1)
#write.net(file = './salidas/insurance.net', insurance.fit)¿Cómo interpretar esta gráfica? Vemos por ejemplo como mucho de la asociación entre edad y tipo de accidente desaparece cuando condicionamos a calidad de conductor.
prop.table(table(insurance$Age, insurance$Accident), margin = 1)
#>
#> Mild Moderate None Severe
#> Adolescent 0.12136878 0.11718365 0.57336288 0.18808469
#> Adult 0.08442918 0.07797973 0.73314348 0.10444761
#> Senior 0.05926482 0.04926232 0.81370343 0.07776944
prop.table(table(insurance$Age, insurance$Accident, insurance$DrivQuality),
margin = c(1, 3))
#> , , = Excellent
#>
#>
#> Mild Moderate None Severe
#> Adolescent 0.011627907 0.001937984 0.982558140 0.003875969
#> Adult 0.011175899 0.004373178 0.981535471 0.002915452
#> Senior 0.004488330 0.003590664 0.988330341 0.003590664
#>
#> , , = Normal
#>
#>
#> Mild Moderate None Severe
#> Adolescent 0.016764459 0.013411567 0.961441744 0.008382230
#> Adult 0.022364771 0.011095700 0.960124827 0.006414702
#> Senior 0.025309917 0.013946281 0.955578512 0.005165289
#>
#> , , = Poor
#>
#>
#> Mild Moderate None Severe
#> Adolescent 0.198470038 0.195070123 0.286867828 0.319592010
#> Adult 0.208120593 0.208606856 0.290542183 0.292730367
#> Senior 0.192834563 0.174920969 0.319283456 0.312961012También podemos entender cómo depende calidad de conductor de edad y aversión al riesgo (modelo local para DrvQuality):
prop_tab_q <- prop.table(table(insurance$DrivQuality, insurance$RiskAversion,
insurance$Age), c(2, 3))
prop_tab_q
#> , , = Adolescent
#>
#>
#> Adventurous Cautious Normal Psychopath
#> Excellent 0.18324079 0.16666667 0.04441703 0.21951220
#> Normal 0.17617365 0.35185185 0.43491672 0.07317073
#> Poor 0.64058556 0.48148148 0.52066626 0.70731707
#>
#> , , = Adult
#>
#>
#> Adventurous Cautious Normal Psychopath
#> Excellent 0.28822140 0.22950127 0.09635941 0.25161290
#> Normal 0.24130948 0.47041420 0.60712626 0.13548387
#> Poor 0.47046912 0.30008453 0.29651433 0.61290323
#>
#> , , = Senior
#>
#>
#> Adventurous Cautious Normal Psychopath
#> Excellent 0.25153374 0.37506065 0.15816327 0.25000000
#> Normal 0.18711656 0.49199418 0.54591837 0.11363636
#> Poor 0.56134969 0.13294517 0.29591837 0.63636364
df_q <- data.frame(prop_tab_q)
names(df_q) <- c('DrvQuality', 'RiskAversion', 'Age', 'Prop')
ggplot(df_q, aes(x = Age, y = Prop, colour = RiskAversion,
group = RiskAversion)) +
geom_line() + facet_wrap(~DrvQuality) +
geom_point()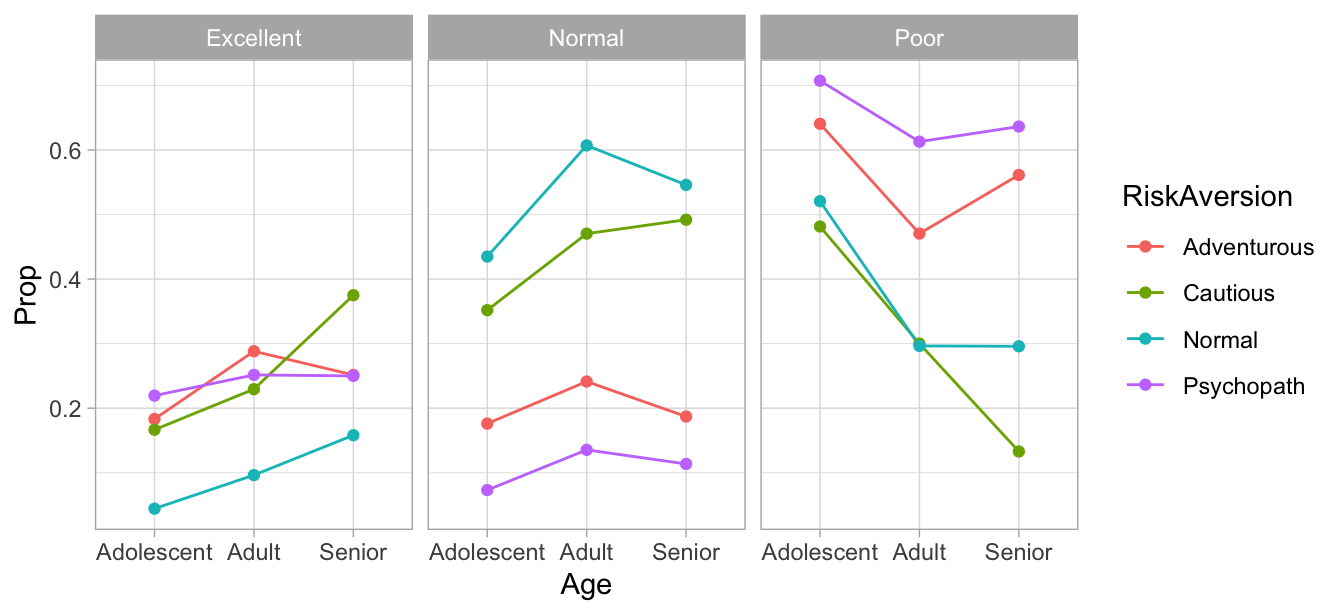
Otras asociaciones con DrvQuality podemos entenderlas a través de estas dos variables: edad y aversión al riesgo. Veremos cómo modelar estas estructuras (además de usar las tablas, que corresponden a estimación de máxima verosimilitud sin restricciones, podemos usar por ejemplo GLMs).
1.1.2 ¿Por qué modelos gráficos?
Usando modelos gráficos podemos representar de manera compacta y atractiva distribuciones de probabilidad entre variables aleatorias.
- Auxiliar en el diseño de modelos.
- Fácil combinar información proveniente de los datos con conocimiento de expertos.
Proveen un marco general para el estudio de modelos más específicos. Muchos de los modelos probabilísticos multivariados clásicos son casos particulares del formalismo general de modelos gráficos (mezclas gaussianas, modelos de espacio de estados ocultos, análisis de factores, filtro de Kalman,…).
Juegan un papel importante en el diseño y análisis de algoritmos de aprendizaje máquina.