9.9 Diagnósticos generales
Cuando generamos una muestra de la distribución posterior usando MCMC, sin importar el método (Metrópolis, Gibbs, HMC), buscamos que:
Los valores simulados sean representativos de la distribución posterior, esto implica que no deben estar influenciados por el valor inicial (arbitrario) y deben explorar todo el rango de la posterior.
Debemos tener suficientes simulaciones de tal manera que las estimaciones sean precisas y estables.
Queremos tener un método eficiente para generar las simulaciones.
En la práctica intentamos cumplir lo más posible estos objetivos, pues aunque en principio los métodos MCMC garantizan que cadena infinitamente largas lograran una representación perfecta, siempre debemos tener un criterio para cortar la cadena y evaluar la calidad de las simulaciones.
Representatividad
Para determinar la convergencia de la cadena es conveniente realizar más de una cadena, buscamos ver si realmente se ha olvidado el estado inicial y revisar que algunas cadenas no hayan quedado atoradas en regiones inusuales del espacio de parámetros.
jags_fit <- jags(
model.file = "codigo_jags/modelo_normal.bugs", # modelo de JAGS
inits = rerun(3, jags_inits()), # valores iniciales
data = list(x = x, N = N), # lista con los datos
parameters.to.save = c("mu", "nu", "sigma2"), # parámetros por guardar
n.chains = 3, # número de cadenas
n.iter = 50, # número de pasos
n.burnin = 0, # calentamiento de la cadena
n.thin = 1
)
#> Compiling model graph
#> Resolving undeclared variables
#> Allocating nodes
#> Graph information:
#> Observed stochastic nodes: 50
#> Unobserved stochastic nodes: 2
#> Total graph size: 62
#>
#> Initializing model
# podemos ver las cadenas
traceplot(jags_fit, varname = c("mu", "sigma2"))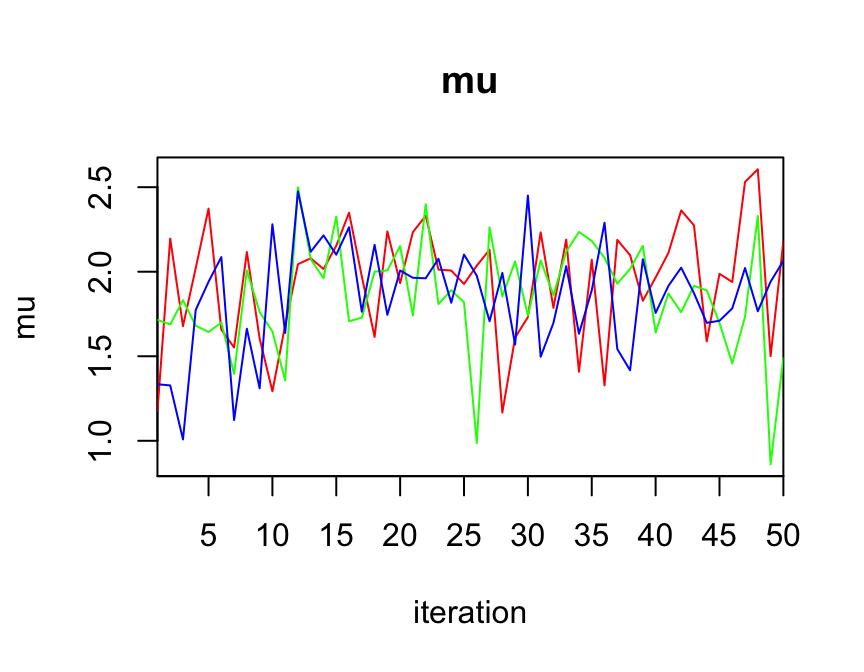
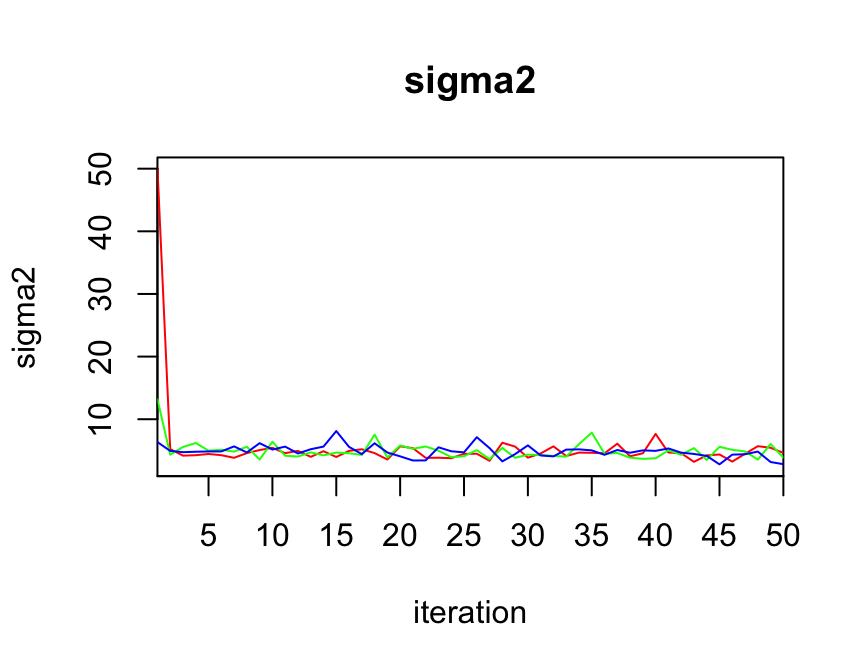
La gráfica anterior nos puede ayudar a determinar si elegimos un periodo de calentamiento adecuado o si alguna cadena está alejada del resto.
Además de realizar gráficas podemos usar la medida de convergencia \(\hat{R}\)
que la función jags() calcula por omisión:
jags_fit$BUGSoutput$summary
#> mean sd 2.5% 25% 50%
#> deviance 224.0517415 6.1828376 221.5063839 221.9263306 222.7528943
#> mu 1.8828510 0.3265556 1.1544683 1.6969239 1.9310980
#> nu 0.2152614 0.0458797 0.1297554 0.1879526 0.2144148
#> sigma2 5.1244415 3.8583574 3.2270859 4.1745253 4.6638571
#> 75% 97.5% Rhat n.eff
#> deviance 224.5585950 231.2154095 1.192520 150
#> mu 2.1000292 2.4572103 1.004371 150
#> nu 0.2395482 0.3098771 1.055707 150
#> sigma2 5.3204898 7.7068088 1.055707 150La medida \(\hat{R}\) se conoce como el factor de reducción potencial de escala o diagnóstico de convergencia de Gelman-Rubin, esta es una estimación de la posible reducción en la longitud de un intervalo de confianza si las simulaciones continuran infinitamente. \(\hat{R}\) es aproximadamente la raíz cuadrada de la varianza de todas las cadenas juntas dividida entre la varianza dentro de cada cadena. Si \(\hat{R}\) es mucho mayor a 1 esto indica que las cadenas no se han mezclado bien. Una regla usual es iterar hasta alcanzar un valor \(\hat{R} \leq 1.1\) para todos los parámetros.
\[\hat{R} = \sqrt{\frac{\hat{d}+3}{\hat{d}+1}\frac{\hat{V}}{W}}\]
donde \(B\) es la varianza entre las cadenas, \(W\) es la varianza dentro de las cadenas
\[B = \frac{N}{M-1}\sum_m (\hat{\theta_m} - \hat{\theta})^2\] \[W = \frac{1}{M}\sum_m \hat{\sigma_m}^2\] Y \(\hat{V}\) es una estimación del varianza de posteriro de \(\theta\):
\[\hat{V} = \frac{N-1}{N}W + \frac{M+1}{MN}B\]
Precisión
Una vez que tenemos una muestra representativa de la distribución posterior, nuestro objetivo es asegurarnos de que la muestra es lo suficientemente grande para producir estimaciones estables y precisas de la distribución.
Para ello usaremos otra salida de la función jags: n.eff que es el
tamaño efectivo de muestra, si las simulaciones fueran independientes
n.eff sería el número total de simulaciones; sin embargo, las simulaciones de
MCMC suelen estar correlacionadas, el tamaño efectivo nos dice que tamaño de
muestra de observaciones independientes nos daría la misma información que las
simulaciones de la cadena.
\[NEM = \frac{N}{1+2\sum_{k=1}^\infty ACF(k)} \]
Usualmente nos gustaría obtener un tamaño efectivo de al menos \(100\).
Eficiencia
Hay varias maneras para mejorar la eficiencia de un proceso MCMC:
Paralelizar, no disminuimos el número de pasos en las simulaciones pero podemos disminuir el tiempo que tarda en correr.
Cambiar la parametrización del modelo o transformar los datos. En el caso de variables continuas suele ser conveniente centrar los datos, otra opción es utilizar parametrizaciones redundantes.
Adelgazar la muestra: esto nos puede ayudar a disminuir el uso de memoria, consiste en guardar únicamente los \(k\)-ésimos pasos de la cadena y resulta en cadenas con menos autocorrelación (en el caso de la función
jags()el adelgazamiento está controlado por el parámetron.thin).
Recomendaciones generales
Gelman and Hill (2007) recomienda los siguientes pasos cuando uno esta simulando de la posterior:
Cuando definimos un modelo por primera vez establecemos un valor bajo para n.iter por ejemplo \(10\) ó \(50\). La razón es que la mayor parte de las veces los modelos no funcionan a la primera por lo que sería pérdida de tiempo dejarlo correr mucho tiempo antes de descubrir el problema.
Si las simulaciones no han alcanzado convergencia aumentamos las iteraciones a \(500\) ó \(1000\) de tal forma que las corridas tarden segundos o unos cuantos minutos.
Si JAGS tarda más que unos cuantos minutos (para problemas del tamaño que veremos en la clase) y aún así no alcanza convergencia entonces juega un poco con el modelo (por ejemplo intenta transformaciones lineales), Gelman sugiere más técnicas para acelerar la convergencia en el capitulo \(19\) del libro Data Analysis Using Regression and Multilevel/Hierarchical models.
Otra técnica conveniente cuando se trabaja con bases de datos grandes (sobretodo para la parte exploratoria) es trabajar con un subconjunto de los datos, quizá la mitad o una quinta parte.
Referencias
Gelman, Andrew, and Jennifer Hill. 2007. Data Analysis Using Regression and Multilevel/Hierarchical Models. Vol. Analytical methods for social research. New York: Cambridge University Press.