4.2 Matriz de precisión

Los elementos de la diagonal de \(D=\Sigma^{-1}\) pueden interpretarse de la siguiente manera:

  • Los elementos de la diagonal están relacionados con la \(R^2\) de la regresión de la variable correspondiente con respecto a todas las demás: \[D_{ii}= 1/(1-R_i^2)\]
  • Los elementos fuera de la diagonal están relacionados con la correlación parcial entre dos variables. La correlación parcial \(\rho_{ij|resto}\) entre \(X_i\) y \(X_j\) es la correlación entre los residuales de la regresión de \(X_i\) contra el resto de las variables y los residuales de \(X_j\) contra el resto de las variables. Se puede interpretar como la correlación que existe entre \(X_i\) y \(X_j\) cuando mantenemos el resto de las variables fijas. Cuando este coeficiente es mucho más chico que la correlación usual entre \(X_i\) y \(X_j\) quiere decir que una buena parte de la correlación de estas variables puede explicarse debido a variación entre el resto de las variables. Específicamente, \[\rho_{ij|resto}-\frac{D_{ij}}{\sqrt{D_{ii}D_{jj}}}.\]

Notemos que no es lo mismo que la correlación usual entre STAT y MECH.

Podemos examinar todas las correlaciones parciales haciendo:

En cada una de las imágenes de abajo indica si la estructura de la gráfica del lado derecho corresponde a la matriz de correlación parcial (cuadro indica valor distinto a cero y vacío indica cero).
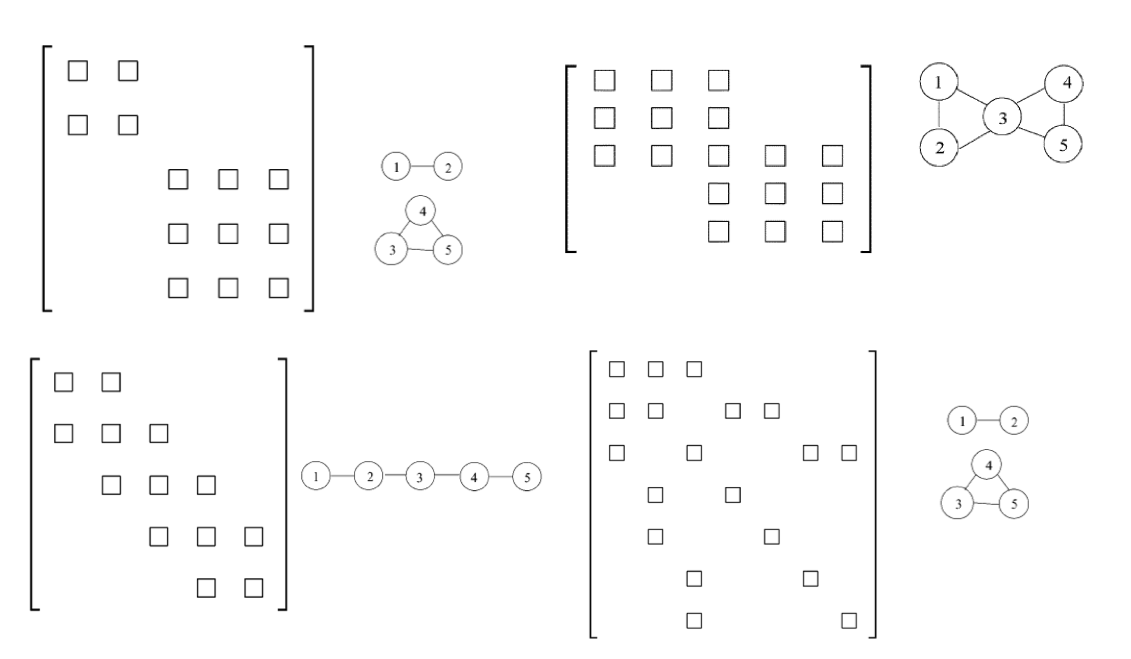a. Arriba izquierda: Verdadero
b. Arriba derecha: Verdadero
c. Abajo izquierda: Verdadero
d. Abajo derecha: Verdadero

4.2.1 Independencia condicional para la normal multivariada

De la discusión anterior, vemos que cuando \((X_1,\ldots, X_k)\) es normal multivariada, entonces \(X_i\) es independiente de \(X_j\) dado el resto de las variables si y sólo si la correlación parcial es cero, o de otra forma, cuando \(D_{ij}=0\).

Podemos ahora apelar a nuestros resultados anteriores (propiedades de Markov por pares, global y distribución de Gibbs) para demostrar el siguiente teorema (aunque también se puede resolver mediante cálculo):

Si \(X=(X_a,X_b, X_c)\) es normal multivariada, donde \(X_a,X_b,X_c\) son bloques de variables. Los vectores \(X_a\) y \(X_b\) son condicionalmente independientes dado \(X_c\) si y sólo si el bloque \(D_{ab}\) de la precisión o varianza inversa \(D=\Sigma^{-1}\) es igual a cero.

Si estandarizamos las variables para que la variabilidad sea comparable, obtenemos la matriz

Cuya inversa es

Donde vemos los coeficientes de esta inversa para los pares ANL-MECH, ANL-VECT, VEC-STAT, MECH-STAT son cercanos a cero. Esto implica que son variables cercanas a la independencia dado el resto de las variables. Así que un modelo apropiado para estos datos tiene todas las aristas, excepto la lista que mencionó arriba. Terminamos entonces con la gráfica

Podemos graficar mostrando las correlaciones parciales:

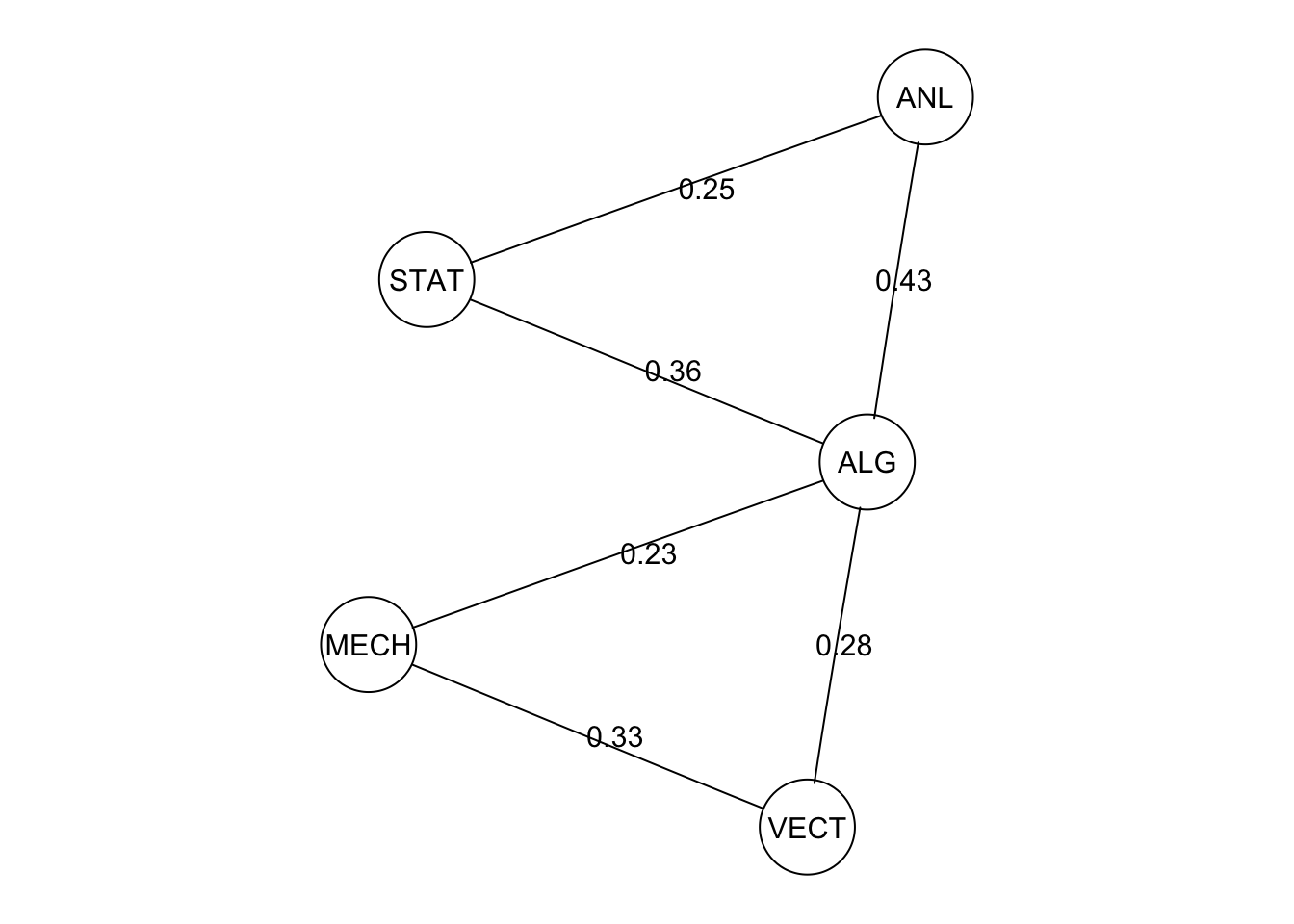
4.2.2 Estimación de máxima verosimilitud con estructura conocida

Un modelo no dirigido gaussiano especifica una distribución normal bivariada \(N(\mu, \Sigma)\) tal que
* Si no hay una arista entre \(X_i\) y \(X_j\), entonces \(D_{ij}=D_{ji}=0\) donde \(D=\Sigma^{-1}\).

De esta forma, vemos que cuando tenemos una estructura no dirigida dada, nuestro trabajo es estimar la matriz de covarianza (o la precisión) con restricciones de ceros dadas por las independencias condicionales.

Podemos entonces maximizar la verosimilitud con las restricciones sobre la inversa de la matriz de varianza y covarianza. En general no es problema trivial.