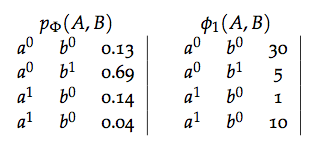3.1 Definiciones y propiedades
Comenzamos estableciendo conceptos y propiedades necesarios para entender las redes markovianas.
3.1.1 Propiedad markoviana por pares
Consideramos variables aleatorias discretas \(X_1, \ldots, X_k\) con una función de distribución conjunta \(p(x_1,\ldots, x_k)\). Supondremos, para simplificar la discusión, que \[p(x_1,x_2,\ldots, x_k)>0\] para cualquier combinación de \(x_1,\ldots, x_k\).
Un primer enfoque es construir una gráfica \(\mathcal M\) no dirigida de la siguiente forma:
Decimos que \({\mathcal M}\) tiene la propiedad Markoviana por pares respecto a la distribución \(p\) cuando es una red no dirigida con vértices \(X_1, \ldots, X_k\) tal que: \(\mathcal M\) no tiene arista entre \(X_i\) y \(X_j\) si y sólo si \(X_i\) y \(X_j\) son independendientes dado el resto de variables aleatorias.
Es decir, existe un arco solamente cuando existe una relación directa entre las dos variables no mediada por dependencia entre otras variables.
Ejemplos.
Consideremos tres variables aleatorias: \(X,Y,Z\). Hay tres posibles
independencias condicionales por pares a considerar: \(X\bot Y|Z\), \(X\bot Z|Y\) y
\(Y\bot Z|Y\). Si ninguna se cumple, la gráfica es completa:
library(gRbase)
library(Rgraphviz)
library(igraph)
library(gRim)
miPlot <- function(x, ...){
V(x)$size <- 55
V(x)$label.cex <- 1.5
V(x)$color <- "salmon"
plot(x)
}
ug_ej1 <- ug(c("X", "Y"), c("Y", "Z"), c("X", "Z"), result = "igraph")
miPlot(ug_ej1)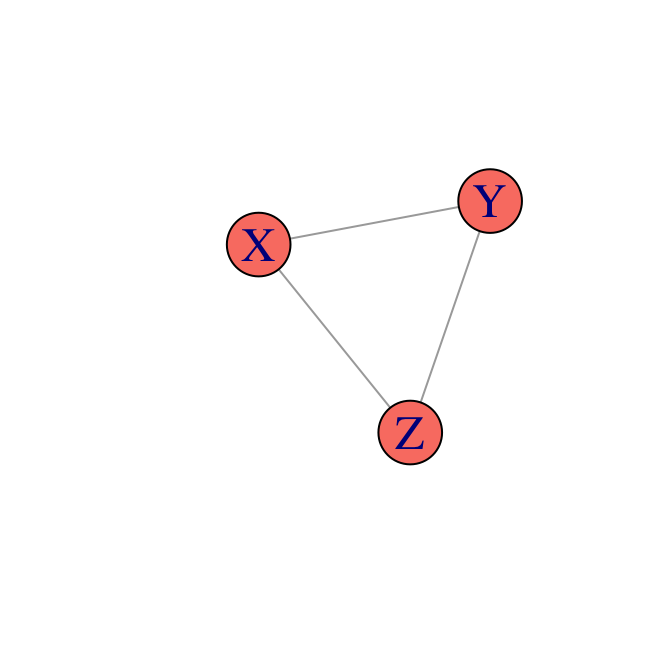
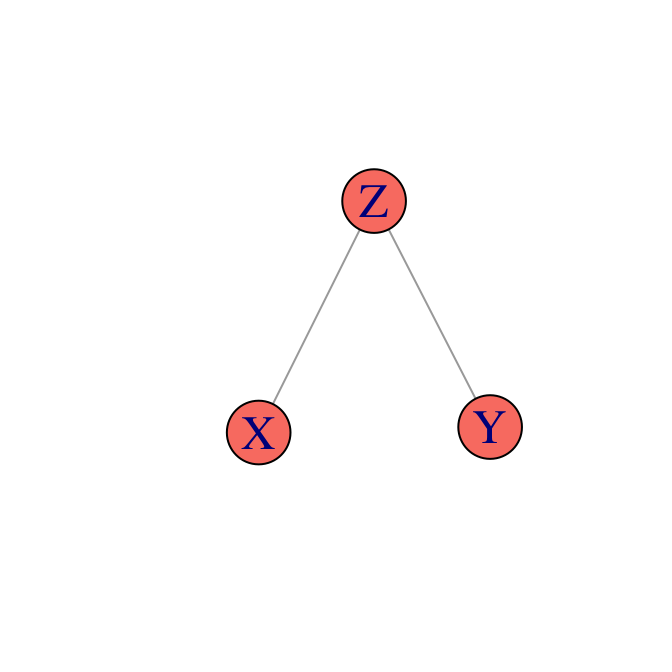
Si se cumple solamente \(X\bot Y|Z\), entonces tenemos
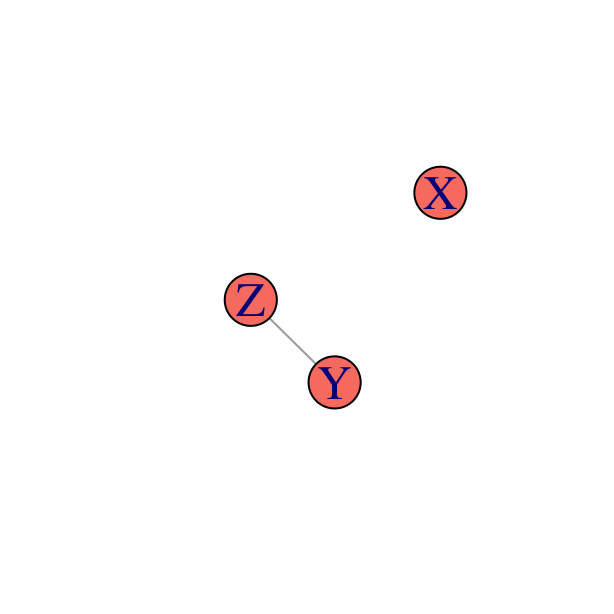
Si se cumplen solamente \(X\bot Y|Z\) y \(X\bot Z|Y\)
3.1.2 Propiedad markoviana global
¿Qué otras propiedades de independencia condicional se pueden leer de esta gráfica? La regla es más fácil que la de redes dirigidas, donde teníamos que tener cuidado con caminos activados por un colisionador. En redes no dirigidas, el concepto de separación es directo:
Sea \(C\) un conjunto de vértices de una red \(\mathcal M\). Decimos que dos vértices \(X\) y \(Y\) están separados por \(C\) en \(\mathcal M\) si todos los caminos no dirigidos entre \(X\) y \(Y\) pasan por algún vértice de \(C\).
Decimos que \(\mathcal M\) satisface la propiedad markoviana global respecto
a \(p\) cuando:
Si \(A,B,C\) son subconjuntos disjuntos de los vértices tal que \(C\) separa a \(A\)
de \(B\), entonces \(A\bot B|C\).
Ejemplo. Consideramos la siguiente gráfica que satiface la propiedad markoviana global para \(p\):
ug_ej4 <- ug( c("X", "Y"), c("X","A"), c('Y','A'), c('A','B'), c('Y','B'),
c('A','Z'), c('Z','W'), c('B','Z'), result = "igraph")
plot(ug_ej4)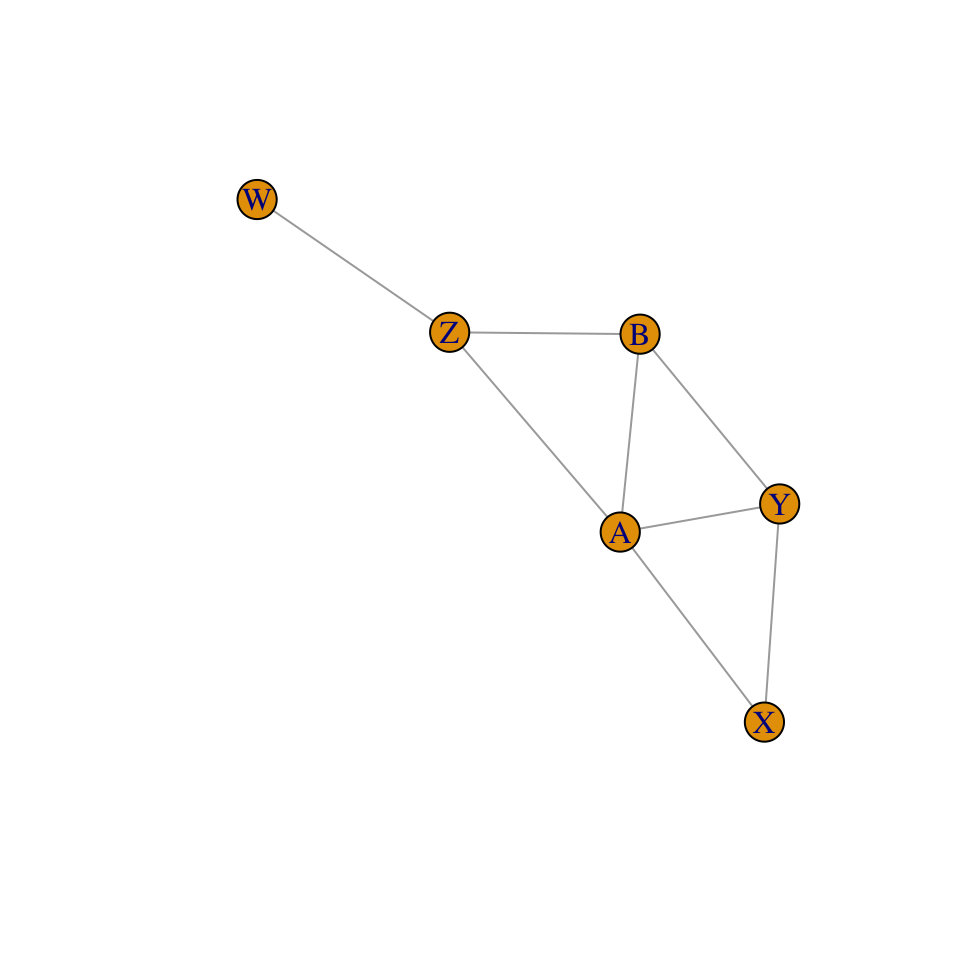 
Podemos leer, por ejemplo, las independencias \(X\bot Z|A,B\), o \(Y\bot W|Z\).
Para distribuciones positivas, tenemos que la propiedad global markoviana es equivalente a la propiedad markoviana por pares.
Esto implica:
* Para una distribución \(p\), podemos construir su red Markoviana asociada
usando la propiedad markoviana por pares.
* Para leer qué otras independencias satisface \(p\), podemos usar la propiedad markoviana global.
3.1.3 Factores y parametrización de redes markovianas
En redes dirigidas vimos que podíamos parametrizar una red bayesiana a través de factores obtenidos de modelos locales de probabilidades condicionales. El caso no dirigido, como veremos, requiere otro tipo de parametrización con base en factores.
Consideremos la red no dirigida \(X\text{--}Z\text{--}Y\). ¿Cómo podemos representar su conjunta (que satisface la independencia de X y Y dado Z y ninguna otra)?
Recordemos que este conjunto de independencias se puede representar de varias maneras con redes dirigidas. Tenemos
\[X\rightarrow Z \rightarrow Y: p(x)p(z|x)p(y|z)\] \[X\leftarrow Z \leftarrow Y: p(y)p(z|y)p(x|z)\] \[X\leftarrow Z \rightarrow Y: p(z)p(x|z)p(y|z)\]
Pero no podemos representarla mediante un colisionador
\[X\rightarrow Z \leftarrow Y: p(x)p(y)p(z|x,y).\]
¿Qué tienen en común las factorizaciones que representan \(X\text{--}Z\text{--}Y\) que es diferente del cuarto caso? En cada uno de los primeros tres casos, podemos factorizar \[p(x,y,z)=\psi_1 (x,z)\psi_2(y,z),\] mientras que no es posible hacer esta factorización en el cuarto caso. Por otra parte, recordamos ahora que precisamente la ecuación anterior es equivalente a independencia condicional de \(X\) y \(Y\) dado \(Z\).
En realidad, para que la independencia condicional se cumpla no es necesario tener igualdad en la ecuación de arriba. Basta que \[p(x,y,z)\propto \psi_1 (x,z)\psi_2(y,z),\] donde los factores \(\psi_1\) y \(\psi_2\) sólo tienen que ser funciones no negativas.
Ejemplo. Consideramos la red no dirigida
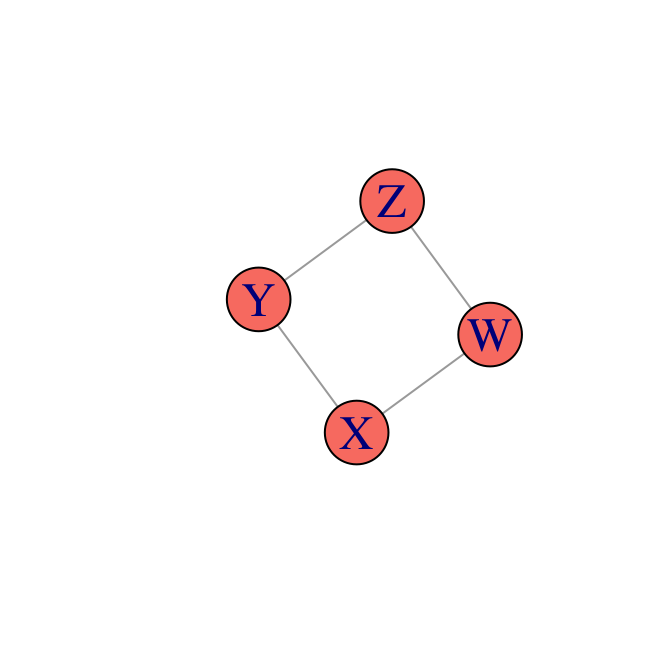
Sabemos que el conjunto de independencias condicionales que satisface esta red no se pueden representar de manera perfecta mediante una red bayesiana. La razón es que cualquier direccionamiento de sus arcos tiene que producir un colisionador, y si hay un colisionador entonces tenemos dependencias que se activan al condicionar.
Usando la idea del ejemplo anterior, podríamos escribir
\[p(x,y,z,w)\propto \psi_1(x,y)\psi_2(y,z)\psi_3(z,w)\psi_4(w,x)\]
donde las funciones \(\psi_i\) son no negativas, sin embargo, el lado derecho no tiene que sumar uno. Normalizando se sigue que \[p(x,y,z,w)=\frac{\psi_1(x,y)\psi_2(y,z)\psi_3(z,w)\psi_4(w,x)}{Z}\] donde \[Z=\sum_{x,y,z,w} \psi_1(x,y)\psi_2(y,z)\psi_3(z,w)\psi_4(w,x)\] es la constante que normaliza el producto de los factores.
Bajo una distribución que se factoriza de esta manera, ¿será cierto que \(X\bot Z|Y,W\)? Un cálculo simple muestra que así es. Tenemos que \[p(x|y,z,w)=\frac{p(x,y,z,w)}{p(y,z,w)}\] La constante de normalización se cancela, así que \[p(x|y,z,w)= \frac{\psi_1(x,y)\psi_2(y,z)\psi_3(z,w)\psi_4(w,x)}{\psi_2(y,z)\psi_3(z,w)\sum_x \psi_1(x,y)\psi_4(w,x)}\] entonces \[p(x|y,z,w)= \frac{\psi_1(x,y)\psi_4(w,x)}{\sum_x \psi_1(x,y)\psi_4(w,x)}.\] Esta cantidad no depende de \(z\), por lo que tenemos \[p(x|y,z,w)=p(x|y,w),\] es decir \(X\bot Z|Y,W\).
Un argumento similar puede darse para \(Y\bot W | X,Z\).
¿La factorización
implica alguna otra independencia condicional? Dando contraejemplos de
distribuciones particulares podemos mostrar que no, para entender la razón
veamos un ejemplo: ¿\(Y\bot W |X\)?. Usando la factorización,
\[p(y|w,x)=\frac{\psi_1(x,y)\sum_z\psi_2(y,z)\psi_3(z,w)} {\sum_y \psi_1(x,y) \left(\sum_z \psi_2(y,z)\psi_3(z,w) \right)},\] donde vemos que en el lado derecho no podemos eliminar la dependencia de \(w\).
Finalmente, bajo este criterio, una red como
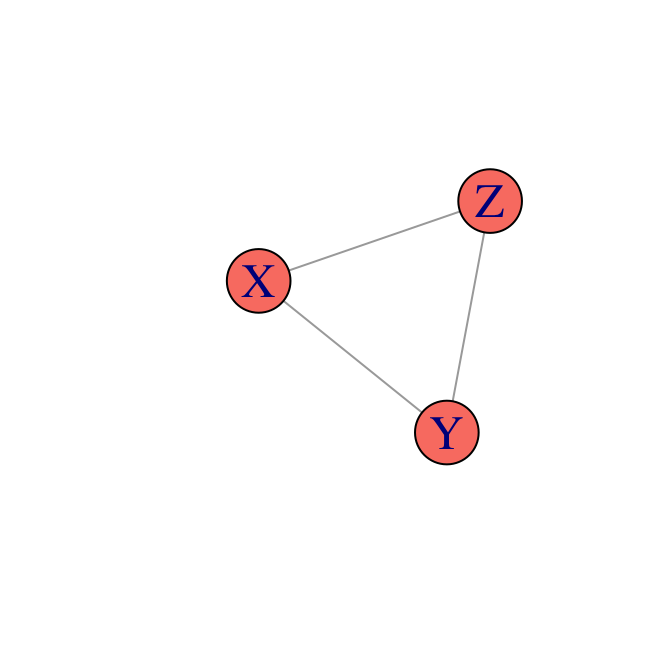
tiene la factorización vacía \[p(x,y,z)\propto \psi(x,y,z),\] pues cualquier otra factorización implicaría independencias condicionales.
Nótese en general que una gráfica completa (donde hay un arco entre cualquier par de vértices) no puede factorizarse de manera no trivial, pues otra vez, esto implicaría independencias condicionales adicionales.
Definimos entonces una subgráfica completa maximal (o cliques) \(\mathcal C\) de \(\mathcal M\) cuando es una subgráfica completa a la que no se le puede agregar ningún nodo adicional y que siga siendo completa. Por ejemplo, en la gráfica
ug_ej7 <- ug(c("X", "Y"), c("Y", "Z"), c("Z", "X"), c('A', 'X'), c('B', 'Y'),
c('B', 'Z'), c('B', 'X'), c('A', 'C'), c('X', 'C'), c('C', 'D'),
c('D', 'E'), result = "igraph")
plot(ug_ej7)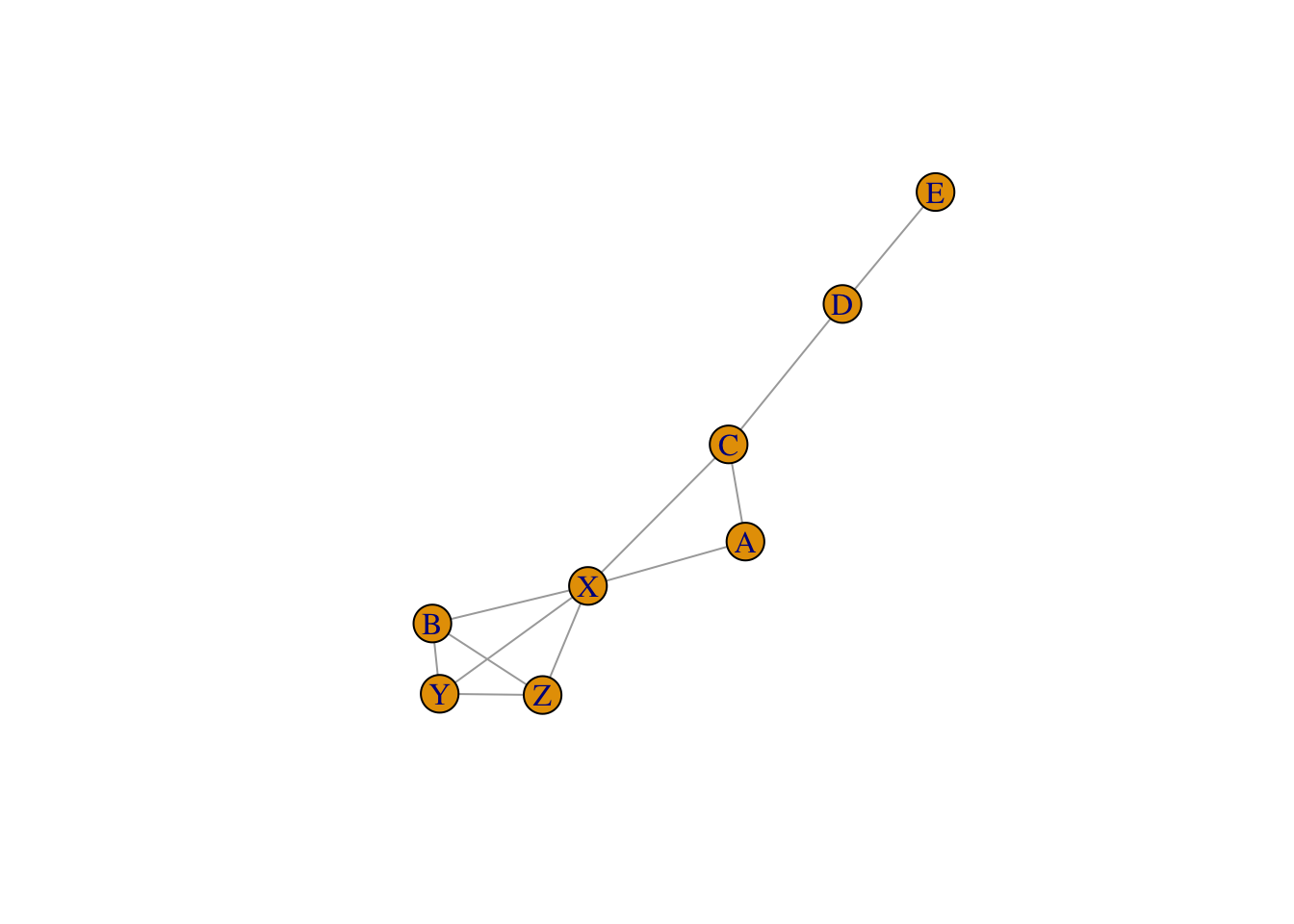 
las subgráficas completas maximales son \(\{X,Y,Z,B\}\), \(\{ X,A,C\}\), \(\{ C,D\}\) y \(\{ D,E\}\). Basta especificar los nodos pues todas ellas son completas.
Distribuciones de Gibbs. Decimos que \(p\) es una distribución de Gibbs respecto a \({\mathcal M}\) si se puede escribir como \[p(x)\propto \prod_{c\in {\mathcal C}} \psi_c (x_c),\] donde \({\mathcal C}\) es el conjunto de cliques de \(\mathcal M\), y cada \(\psi_c\) es un factor (no negativo) que sólo depende de las variables dentro del clique \(c\).
La siguiente figura ejemplifica los de factores sobre cliques.
Obsérvese que de la factorización anterior recuperamos la conjunta normalizando: \[p(x)=\frac{ \prod_{c\in {\mathcal C}} \psi_c (x_c)}{Z},\] donde \(Z\) es el factor de normalización (también llamada función de partición) \[Z=\sum_{x}\prod_{c\in {\mathcal C}} \psi_c (x_c).\]
En las definiciones anteriores hemos escrito el producto de factores:
Sean \(X\), \(Y\) y \(Z\) tres conjuntos disjuntos de variables (esto es, conjuntos con intersección vacía), y sean \(\phi_1(X,Y)\) y \(\phi_2(Y,Z)\) dos factores. Definimos el producto de factores \(\phi_1 \times \phi_2\) como el factor \(\psi:Val(X,Y,Z)\rightarrow \mathbb{R}\): \[\psi(X,Y,Z) = \phi_1(X,Y)\cdot \phi_2(Y,Z)\]
Notemos que tanto las densidades de probabilidad condicional como las distribuciones conjuntas son factores, por ejemplo cuando calculamos la probabilidad conjunta \(p(A,B) = p(A)p(B|A)\) estamos realizando un producto de factores. En redes bayesianas también podemos ver la multiplicación de factores, si definimos \(\phi_{X_i}(X_i,Pa_{X_i}) = p(X_i|Pa_{X_i})\) tenemos \[p(X_1,...,X_n) = \prod_i \phi_{X_i}.\]
Ejemplo. Una distribución \(p\) es Gibbs respecto a la gráfica anterior cuando podemos factorizar \[p(x)\propto \psi_1 (x,y,z,b)\psi_2(x,a,c)\psi_3(c,d)\psi_4(d,e)\]
Esta factorización implica, como hemos visto, ciertas relaciones de independencia condicional. Por ejemplo, podemos demostrar que \(Y\) y \(D\) son condicionalmente independientes dada \(X\):
\[p(y,d,x)=\left( \sum_e\psi_4(d,e) \right) \left( \sum_{a,c}\psi_3(c,d)\psi_2(x,a,c) \right) \left( \sum_{z,b}\psi_1(x,y,z,b) \right)\] y vemos que en el cociente con \(p(d,x)\), se eliminan los factores \(\left( \sum_e\psi_4(d,e) \right) \left( \sum_{a,c}\psi_3(c,d)\psi_2(x,a,c) \right)\). El término restante no depende de \(d\). }
Ahora vemos que la factorización es precisamente la expresión que necesitamos para expresar las independencias condicionales que se leen de la gráfica:
Hammersley-Clifford. Sea \(p\) una distribución positiva. Entonces \(p\) es Gibbs en relación a \(\mathcal M\) si y sólo si \(\mathcal M\) satisface la propiedad global de Markov respecto a \(p\).
Entonces, de manera similar a gráficas dirigidas vimos dos maneras de caracterizar los modelos gráficos no dirigidos:
Dada una gráfica \(\mathcal M\), todas las distribuciones que se pueden expresar como el producto de factores (o potenciales) definidos sobre cliques (subgráficas completas maximales).
Dada una gráfica \(\mathcal M\), todas las distribuciones que satisfacen todas las independencias que especifica la gráfica.
Hammersley-Clifford: Las dos caracterizaciones son equivalentes.
Para la siguiente gráfica ¿Que
afirmaciones de independencia están en I(\(\mathcal{M}\)), es decir que
independencias están inducidas por la gráfica?
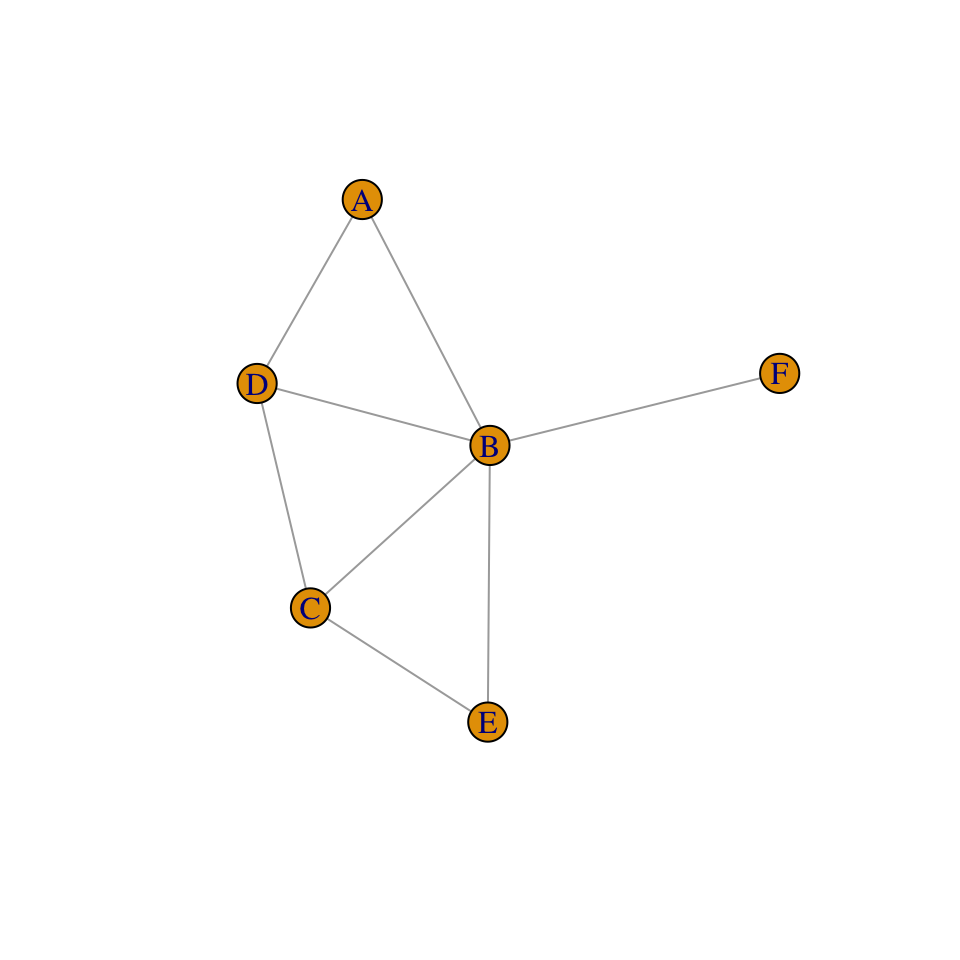
- (\(A \bot C| B,D\))
- (\(A\bot E| B\))
- (\(C\bot F|B\))
- (\(A \bot F|B,D\))
- Ninguna.
3.1.4 Factores y parametrización
Ejemplo (juguete). Supongamos que hay cuatro estudiantes que se reunen en pares para trabajar en una tarea; por varias razones únicamente se reunen los pares Ana y Carla, Ana y Benito, Benito y Daniel, Carla y Daniel (las parejas de estudio se representan en la gráfica inferior). En este ejemplo el profesor comete un error en clase, y cada estudiante puede haber elicitado el error o haber retenido el error. Cuando se reúnen a estudiar en parejas, un estudiante que encontró el error puede aclararlo a su pareja. Definimos entonces 4 variables aleatorias {\(A,B,C,D\)}, denotemos \(a^0\) si Ana aclaró el error y \(a^1\) si lo retiene, similarmente \(b^0,b^1,c^0,...\). Debido a que Ana y Daniel nunca son equipo queremos modelar una distribución que satisface (\(A\perp D|B,C\)) y similarmente (\(B \perp C | A,D\)).
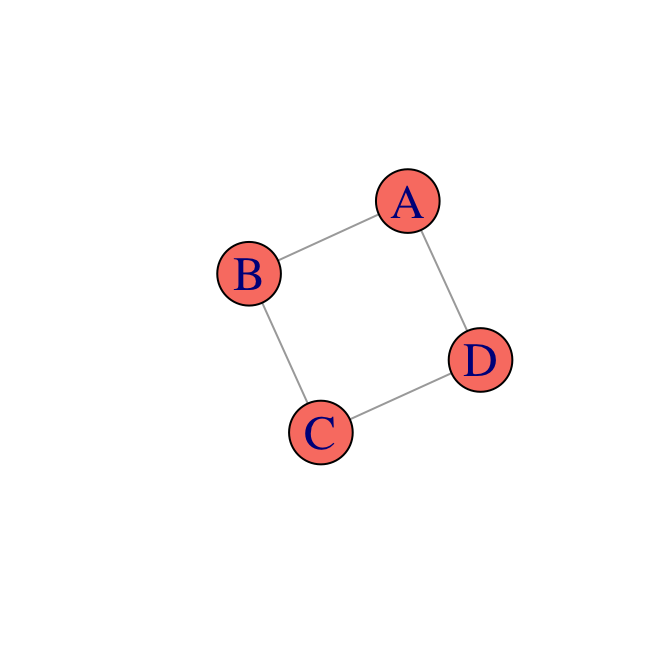
Describimos la relación entre Ana y Benito mediante un factor \(\phi_1(A,B):Val(A,B)\rightarrow \mathbb{R}^+\), donde el valor de cada asignación \((a,b)\) corresponde a la \(afinidad\) entre los dos valores, un mayor valor \(\phi_1(a,b)\) indica mayor compatibilidad entre \(a\) y \(b\).
¿Por qué
\(\phi_1(a,b)\cdot \phi_2(b,c) \cdot \phi_3(c,d)\cdot\phi_4(d,a)\) no es
una distribución de probabilidad?
a. Puede ser negativo.
b. No necesariamente está entre 0 y 1.
c. No suma uno (\(\sum_{a b c d}\phi_1(a,b)\cdot \phi_2(b,c) \cdot \phi_3(c,d)\cdot\phi_4(d,a)\)).
d. Faltan factores para determinar la distribución (ej. \(\phi_1(a,c)\))
De manera similar a las redes bayesianas, debemos combinar los modelos locales para definir el modelo global; sin embargo, la multiplicación de los factores no tiene porque definir una distribución por lo que es necesario normalizar el producto de factores.
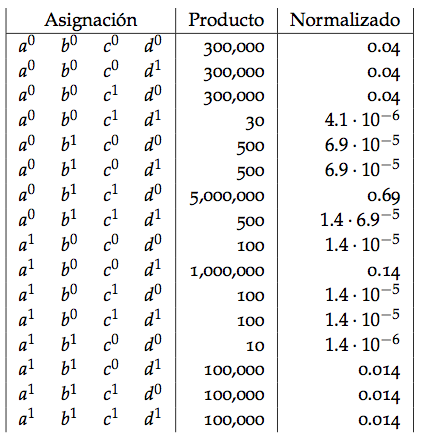
En el ejemplo de los estudiantes definimos: \[ p(a,b,c,d) = \frac{1}{Z}\phi_1(a,b)\cdot \phi_2(b,c) \cdot \phi_3(c,d)\cdot\phi_4(d,a)\] donde \[Z = \sum_{a,b,c,d} \phi_1(a,b)\cdot \phi_2(b,c) \cdot \phi_3(c,d) \cdot \phi_4(d,a)\] es la constante de normalización que también se conoce como función de partición.
Calculamos la distribución de probabilidad conjunta multiplicando los factores y normalizando como sigue: \[ p(a,b,c,d) = \frac{1}{Z}\phi_1(a,b)\cdot \phi_2(b,c) \cdot \phi_3(c,d)\cdot\phi_4(d,a)\] donde \[Z = \sum_{a,b,c,d} \phi_1(a,b)\cdot \phi_2(b,c) \cdot \phi_3(c,d) \cdot \phi_4(d,a)\] es la constante de normalización.
Obtenemos así la siguiente tabla que describe la distribución conjunta de las variables aleatorias:
3.1.4.1 Parametrización
Para representar una distribución necesitamos asociar la estructura de la gráfica con un conjunto de parámetros de manera similar a como las funciones de densidad condicional parametrizan las gráficas dirigidas. Sin embargo, la parametrización de redes markovianas no es tan intuitiva ya que los factores no corresponden a probabilidades, esto conlleva a que los parámetros sean difíciles de entender y por tanto no es fácil elicitarlos de expertos. Para entender que la relación entre los factores y la distribución de probabilidad no se relacioan de manera intutiva comparemos el factor \(\phi_1(A,B)\) con la distribución marginal \(p_\Phi(A,B)\):
Si consideramos el factor \(\phi_1(A,B)\), nos preguntamos si dicho factor es es proporcional a:
a. La probabilidad marginal \(p(A,B)\).
b. La probabilidad condicional \(p(A|B)\).
c. La probabilidad condicional \(p(A,B|C,D)\).
d. Ninguna de las anteriores
Para entender que la relación entre los factores y la distribución de probabilidad no es intutiva comparemos el factor \(\phi_1(A,B)\) con la distribución marginal \(p_\Phi(A,B)\):
