7.2 Modelos markovianos de estados ocultos
Comenzamos con un modelo simple, que consiste de dos variables, una observada y una latente:
- Xt cantidad de lluvia en mm.
- St variable discreta con dos valores posibles: soleado o nublado.
El modelo está definido en dos grandes partes
Modelo de observaciones: P(Xt|St). Este modelo está dado con dos densidades: una para la cantidad de lluvia cuando St=nublado y otra para St=soleado.
Modelo de transición de estados: P(St+1|St). Estos modelos están dados por una matriz de transición, pues supondremos que estas probabildades no cambian con t (supuesto de homogeneidad). Por ejemplo, podríamos tener:
p_trans <- matrix(c(0.8, 0.2, 0.3, 0.7), byrow = T, ncol = 2)
p_trans
#> [,1] [,2]
#> [1,] 0.8 0.2
#> [2,] 0.3 0.7Y el modelo completo se puede representar como la última gráfica de la sección anterior.
En este ejmplo, el modelo de observaciones es Xt normal con media 20 y desviación estándar 5 cuando se trata de un día soleado, y Xt es normal con media 100 y desviación estándar 20 cuando se trata de un día nublado.
set.seed(2805)
estadosLluvia <- function(n){
estado <- character(n)
estado[1] <- sample(c('soleado', 'nublado'), 1)
transicion <- matrix(c(0.8, 0.2, 0.2, 0.8), 2, byrow = T)
rownames(transicion) <- c('soleado', 'nublado')
colnames(transicion) <- c('soleado', 'nublado')
for(j in 2:n){
estado[j] <- sample(c('soleado', 'nublado'), 1,
prob = transicion[estado[j - 1], ])
}
estado
}
estadosLluvia(10)
#> [1] "nublado" "nublado" "nublado" "nublado" "nublado" "nublado" "nublado"
#> [8] "soleado" "soleado" "soleado"
prob_obs <- tibble(edo = c("soleado", "nublado"), medias = c(20, 100),
desv = c(10, 50))
obsPrecip <- function(long_serie){
tibble(dia = 1:long_serie, edo = estadosLluvia(long_serie)) %>%
left_join(prob_obs) %>%
mutate(
precipit = rnorm(1:long_serie, medias, desv),
precipit = ifelse(precipit < 0, 0, precipit)
)
}
ej_1 <- obsPrecip(10)Series simuladas de este modelo se ven como sigue:
sims_1 <- rdply(10, obsPrecip(50))
ggplot(sims_1, aes(x = dia, ymax = precipit, ymin = 0, y = precipit, color = edo)) +
geom_linerange(alpha = 0.6) +
geom_point(size=0.8) +
facet_wrap(~.n, nrow = 2)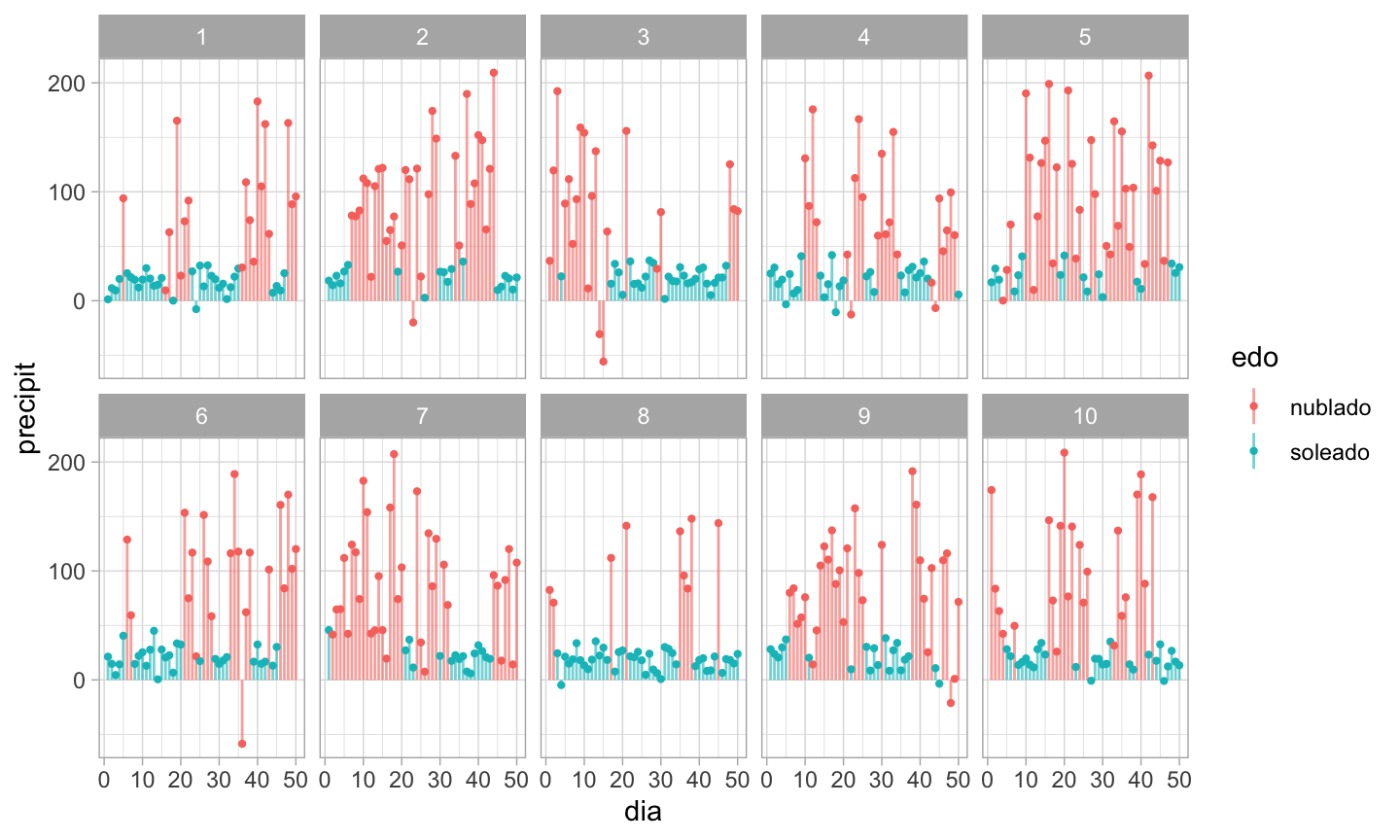
Nótese que hay dependencia secuencial en estos datos. Si sólo tuviéramos los datos observados, podríamos construir un modelo más complejo intentando entender las correlaciones secuenciales:
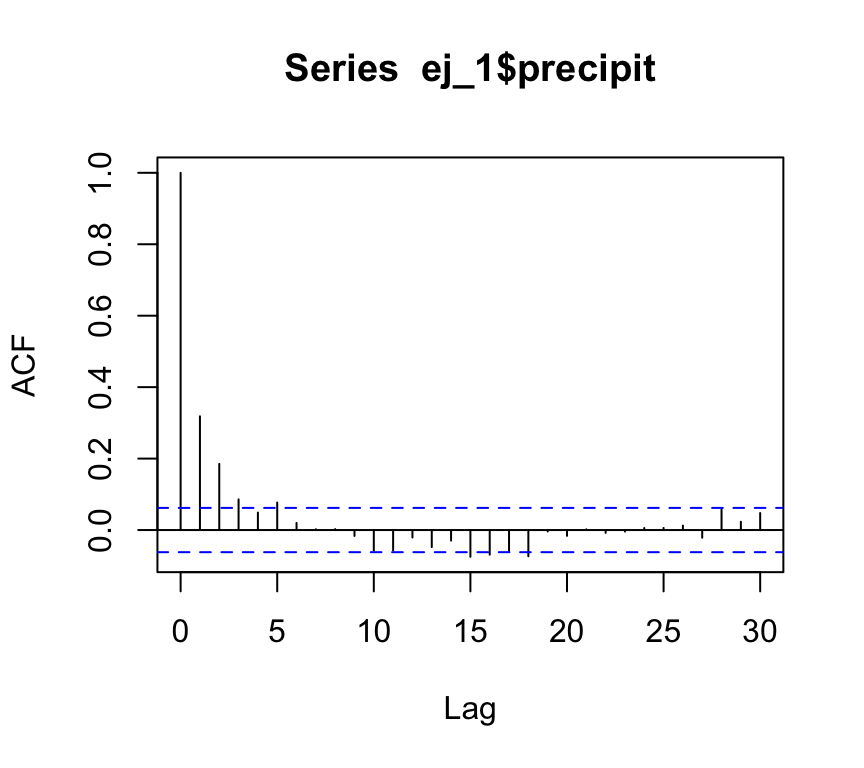
 Ajusta con EM un modelo a estos datos
usando el paquete depmixS4. Prueba con distintos tamaños de muestra. Por ejemplo:
Ajusta con EM un modelo a estos datos
usando el paquete depmixS4. Prueba con distintos tamaños de muestra. Por ejemplo:
library(depmixS4)
datos <- sims_1
# ntimes: son 10 series de longitud 50 cada una:
mod_hmm <- depmix(precipit~1, data=datos, nstates=2,
family=gaussian(), ntimes=rep(50,10))
fit_1 <- fit(mod_hmm, emcontrol=em.control(maxit=200))
#> converged at iteration 22 with logLik: -2448.528
summary(fit_1)
#> Initial state probabilties model
#> pr1 pr2
#> 0.654 0.346
#>
#> Transition matrix
#> toS1 toS2
#> fromS1 0.798 0.202
#> fromS2 0.200 0.800
#>
#> Response parameters
#> Resp 1 : gaussian
#> Re1.(Intercept) Re1.sd
#> St1 19.542 9.717
#> St2 93.407 52.779Observa que como tenemos varias series, podemos estimar las probabilidades iniciales. Cuando tenemos una sola serie, típicamente suponemos que la serie comienza en un estado, por ejemplo el primero.
Consideramos datos secuenciales X1,…,XT. Un modelo markoviano de estado oculto se factoriza como (es decir, cumple las relaciones de independencia condicional indicadas en la gráfica):

Las variables St (estado oculto) son latentes.
Las variables Xt no son independientes, pero son condicionalmente independientes dados los estados ocultos.
El modelo está dado por una factorización que solo incluye términos de la forma P(St|St−1), P(Xt|St) y P(S1).
En los modelos de transición de estados suponemos homogeneidad de la cadena de Markov subyacente, es decir,P(St=j|St−1=i)=pijno depende de t.
- En los modelos de respuesta o de observación, las variables observadas Xt pueden ser discretas o continuas. Si Xt son discretas, cada P(Xt|St) está dada por una tabla, que también suponemos homogénea (no depende de t). Si Xt son continuas, entonces estas probabilidades están dadas por densidades condicionales.
Observación: una generalización usual de homogeneidad es incluir covariables en los modelos de respuesta o de observación, de forma que especificamos P(Xt|St,Zt) con modelos de regresión, por ejemplo. El análisis es condicional a los valores de Zt (no modelamos su dinámica, por ejemplo). También las probabilidades de transición pueden depender de covariables.}
Ejemplo: serie de terremotos. Ahora podemos regresar al ejemplo de los terremotos. Ajustamos los modelos de estado oculto a la serie (de 1 a 4 estados):
library(depmixS4)
terremotos <- data.frame(num = c(13,14,8,10,16,26,32,27,18,32,36,24,22,23,22,18,
25,21,21,14,8,11,14,23,18,17,19,20,22,19,13,26,13,14,22,24,21,22,26,21,23,24,
27,41,31,27,35,26,28,36,39,21,17,22,17,19,15,34,10,15,22,18,15,20,15,22,19,16,
30,27,29,23,20,16,21,21,25,16,18,15,18,14,10,15,8,15,6,11,8,7,18,16,13,12,13,
20,15,16,12,18,15,16,13,15,16,11,11), anio = 1900:2006)
head(terremotos)
#> num anio
#> 1 13 1900
#> 2 14 1901
#> 3 8 1902
#> 4 10 1903
#> 5 16 1904
#> 6 26 1905
modelos_hmm <- lapply(1:4, function(i){
mod_hmm <- depmix(num~1, data = terremotos, nstates = i, family = poisson(),
ntimes = 107)
fit_hmm <- fit(mod_hmm, emcontrol = em.control(maxit = 200))
fit_hmm
})
#> converged at iteration 1 with logLik: -391.9189
#> converged at iteration 28 with logLik: -341.8787
#> converged at iteration 24 with logLik: -328.5275
sapply(modelos_hmm, BIC)
#> [1] 788.5107 707.1216 708.4561 745.1272
sapply(modelos_hmm, AIC)
#> [1] 785.8379 693.7574 679.0550 694.3435Podemos seleccionar el modelo con 3 estados.
mod_1 <- modelos_hmm[[3]]
summary(mod_1)
#> Initial state probabilties model
#> pr1 pr2 pr3
#> 0 0 1
#>
#> Transition matrix
#> toS1 toS2 toS3
#> fromS1 0.810 0.190 0.000
#> fromS2 0.053 0.906 0.040
#> fromS3 0.029 0.032 0.939
#>
#> Response parameters
#> Resp 1 : poisson
#> Re1.(Intercept)
#> St1 3.392
#> St2 2.981
#> St3 2.575Simulaciones de este modelo dan los siguiente resultados, en donde es difícil distinguir los datos observados:
class(mod_1) <- 'depmix'
set.seed(2805)
sims_1 <- simulate(mod_1, nsim = 19)
terremotos_null <- data.frame(num = sims_1@response[[1]][[1]]@y,
anio = rep(terremotos$anio, 19)) %>%
rbind(terremotos)
codigo <- sample(1:20)
terremotos_null$tipo <- rep(codigo, each = 107)
ggplot(terremotos_null, aes(x = anio, y = num)) +
geom_line(size=0.3) +
facet_wrap(~tipo)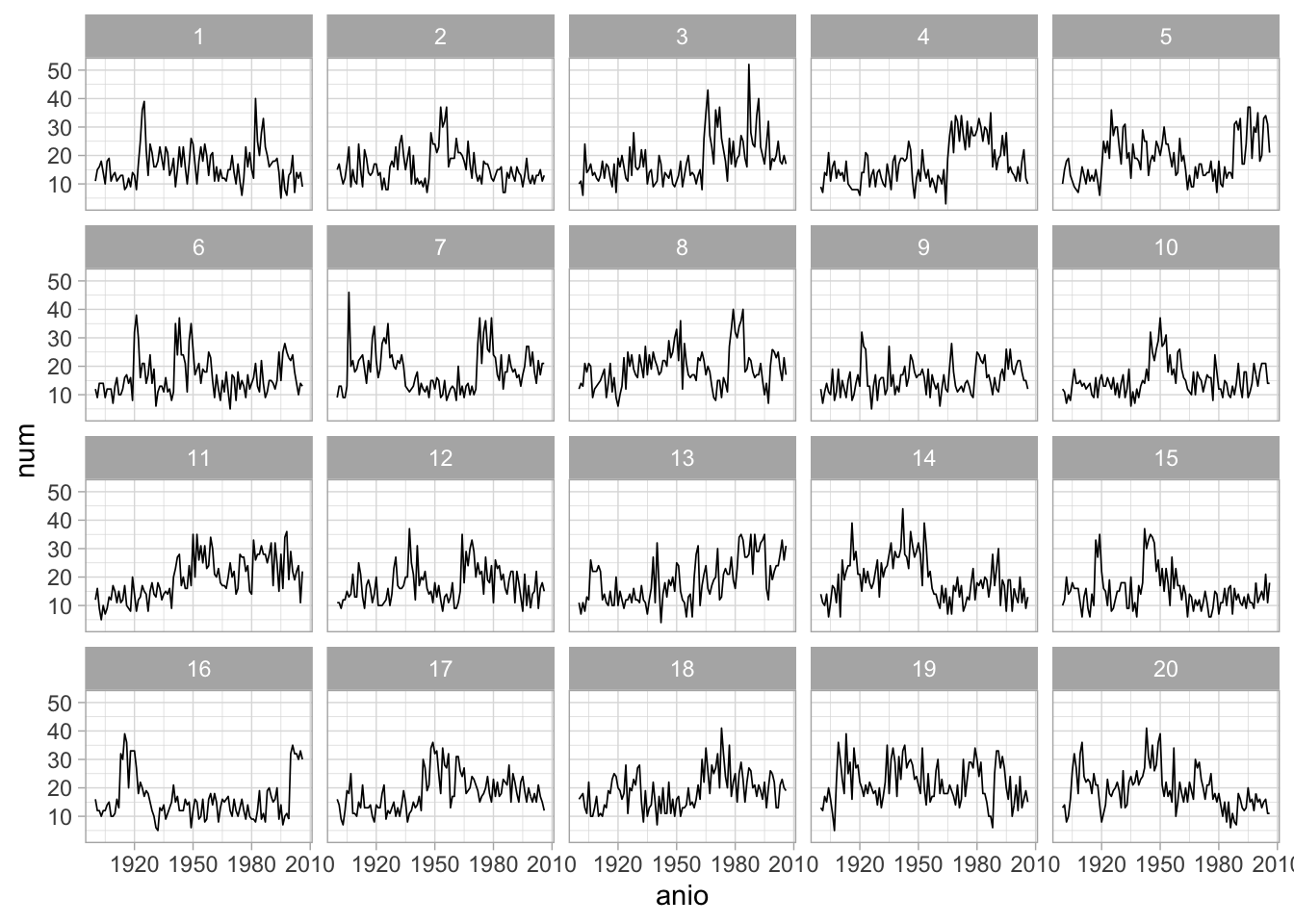
Vemos que las autocorrelaciones de grado 1 son similares:
terremotos_null %>%
group_by(tipo) %>%
mutate(num_lag = lag(num)) %>%
filter(!is.na(num_lag)) %>%
summarise(cor = cor(num, num_lag))
#> cor
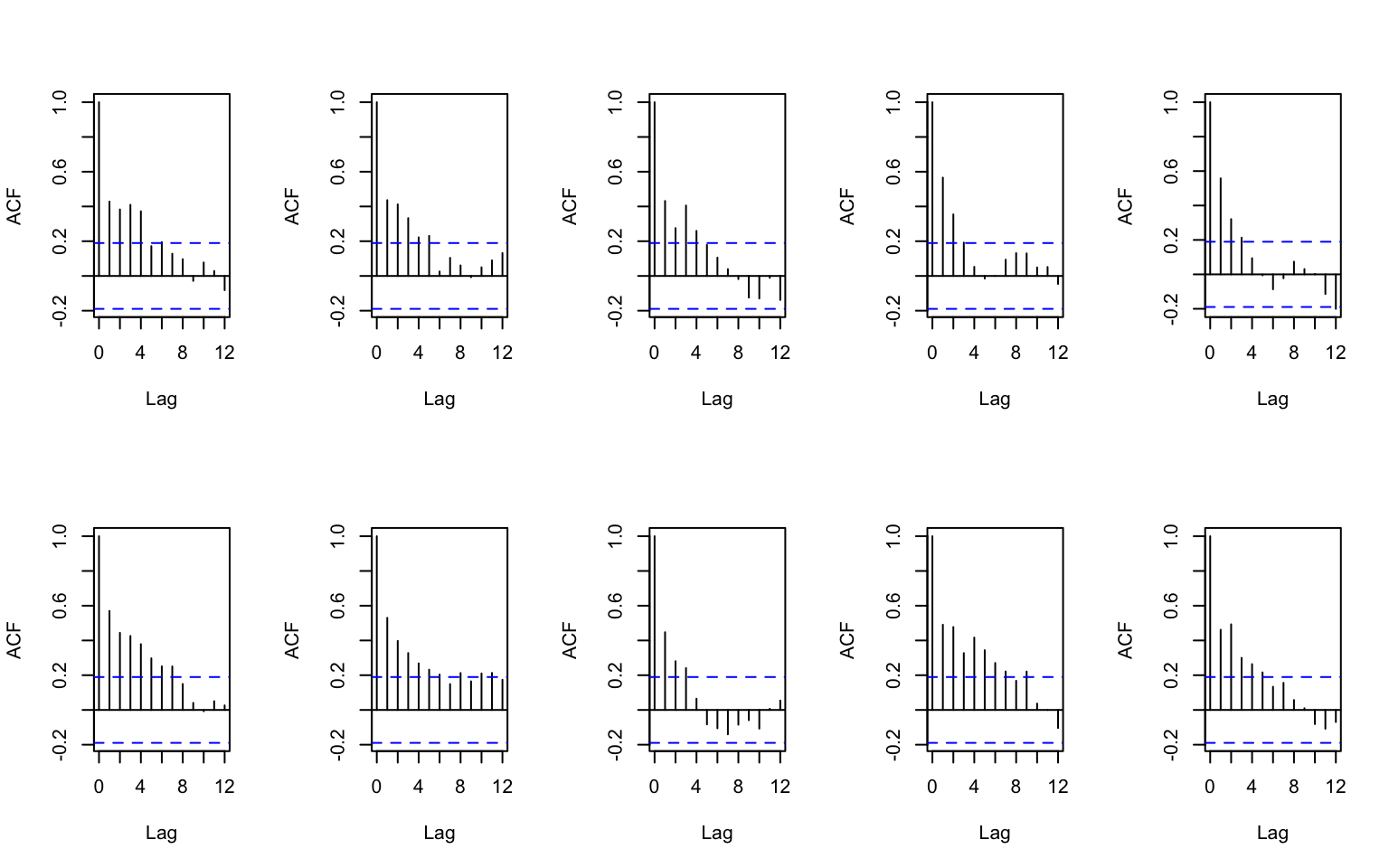
#> 1 0.557025E incluso podemos comparar las gráficas de autocorrelación, que no muestran desajuste importante:
set.seed(227342)
# solo 10 gráficas
sims_1 <- simulate(mod_1, nsim = 9)
terremotos_null <- data.frame(num = sims_1@response[[1]][[1]]@y,
anio = rep(terremotos$anio, 9)) %>%
rbind(terremotos)
codigo <- sample(1:10)
terremotos_null$tipo <- rep(codigo, each = 107)
par(mfrow=c(2, 5))
sims_x <- ddply(terremotos_null, 'tipo', function(df){
x <- df$num
acf(x, lag.max=12, main="")
x
})
Podemos ver el desempeño de estos modelos en predicción:
set.seed(72)
preds_2 <- sapply(50:106 ,function(i){
dat.1 <- terremotos[1:i,,drop=FALSE]
mod.1 <- depmix(num ~ 1, data = dat.1, nstates = 3, family = poisson(),
ntimes = i)
fit.mod.1 <- fit(mod.1, verbose = FALSE, emcontrol=em.control(maxit=600))
probs.1 <- fit.mod.1@posterior[i, 2:4]
#estado.i <- sample(1:3, 1, prob = probs.1)
estado.i <- fit.mod.1@posterior[i, 1]
estado.pred <- which.max(predict(fit.mod.1@transition[[estado.i]]))
fit.mod.1@response[[estado.pred]][[1]]@parameters[1]$coefficients
})
#> converged at iteration 36 with logLik: -155.3172
#> converged at iteration 151 with logLik: -159.4318
#> converged at iteration 58 with logLik: -163.1262
#> converged at iteration 82 with logLik: -166.54
#> converged at iteration 79 with logLik: -169.1791
#> converged at iteration 99 with logLik: -172.0019
#> converged at iteration 63 with logLik: -174.5637
#> converged at iteration 44 with logLik: -177.6554
#> converged at iteration 113 with logLik: -182.8753
#> converged at iteration 69 with logLik: -188.5222
#> converged at iteration 74 with logLik: -191.4006
#> converged at iteration 44 with logLik: -194.564
#> converged at iteration 44 with logLik: -197.228
#> converged at iteration 52 with logLik: -200.332
#> converged at iteration 57 with logLik: -202.9127
#> converged at iteration 74 with logLik: -205.9684
#> converged at iteration 82 with logLik: -208.6685
#> converged at iteration 94 with logLik: -211.2156
#> converged at iteration 91 with logLik: -213.9362
#> converged at iteration 64 with logLik: -218.3898
#> converged at iteration 67 with logLik: -221.6229
#> converged at iteration 69 with logLik: -224.6889
#> converged at iteration 95 with logLik: -227.9049
#> converged at iteration 90 with logLik: -230.9431
#> converged at iteration 95 with logLik: -233.8692
#> converged at iteration 100 with logLik: -236.4674
#> converged at iteration 124 with logLik: -239.0547
#> converged at iteration 107 with logLik: -242.1658
#> converged at iteration 86 with logLik: -245.0686
#> converged at iteration 69 with logLik: -247.6256
#> converged at iteration 63 with logLik: -250.5989
#> converged at iteration 55 with logLik: -253.1444
#> converged at iteration 49 with logLik: -256.308
#> converged at iteration 55 with logLik: -260.4003
#> converged at iteration 58 with logLik: -263.1498
#> converged at iteration 38 with logLik: -266.5168
#> converged at iteration 39 with logLik: -269.194
#> converged at iteration 32 with logLik: -273.2231
#> converged at iteration 29 with logLik: -275.5442
#> converged at iteration 29 with logLik: -278.3187
#> converged at iteration 32 with logLik: -281.3215
#> converged at iteration 43 with logLik: -285.0577
#> converged at iteration 49 with logLik: -287.9933
#> converged at iteration 34 with logLik: -290.7704
#> converged at iteration 27 with logLik: -293.169
#> converged at iteration 25 with logLik: -295.5334
#> converged at iteration 34 with logLik: -299.51
#> converged at iteration 33 with logLik: -302.3083
#> converged at iteration 33 with logLik: -305.0914
#> converged at iteration 25 with logLik: -307.7153
#> converged at iteration 32 with logLik: -310.9161
#> converged at iteration 26 with logLik: -313.5136
#> converged at iteration 27 with logLik: -316.1973
#> converged at iteration 25 with logLik: -318.5934
#> converged at iteration 27 with logLik: -321.066
#> converged at iteration 28 with logLik: -323.6907
#> converged at iteration 25 with logLik: -326.1425
## error medio absoluto
mean(abs(exp(preds_2) - terremotos[51:107,"num"]))
#> [1] 4.699983Finalmente, comparamos con la predicción de tomar el valor anterior:
Ejemplo: prototipo reconocimiento de trazo de dígitos. Los modelos de estados escondidos se usan en varias partes de procesamiento de señales. En este ejemplo, veremos un enfoque para reconocer dígitos con base en los trazos que se hacen para escribirlos, este es un enfoque distinto al usual en donde se trabaja con una matriz de pixeles. Utilizaremos los datos pendigits.
load('data/pendigits/digitos_lista.RData')
load('data/pendigits/digitos.RData')
length(results.list)
#> [1] 7494
digito <- results.list[[1]]
digito
#> [,1] [,2]
#> init 267 333
#> 267 336
#> 267 339
#> 266 342
#> 264 344
#> 262 346
#> 259 346
#> 254 347
#> 249 346
#> 244 345
#> 239 343
#> 235 340
#> 233 333
#> 233 327
#> 235 318
#> 239 309
#> 245 297
#> 251 285
#> 258 272
#> 265 259
#> 272 247
#> 277 235
#> 280 223
#> 284 208
#> 284 199
#> 281 192
#> 278 184
#> 272 178
#> 265 171
#> 258 166
#> 249 162
#> 241 158
#> 233 155
#> 225 153
#> 219 152
#> 214 152
#> 210 153
#> 207 155
#> 204 158
#> 202 163
#> 201 169
#> 201 174
#> 202 181
#> 205 188
#> 208 195
#> 213 202
#> 220 209
#> 227 216
#> 236 223
#> 246 229
#> 258 237
#> 268 245
#> 279 252
#> 290 260
#> 301 268
#> 310 277
#> 317 286
#> 323 293
#> 327 300
#> 329 306
#> 330 312
#> 330 317
#> 330 320
#> 329 323
#> 327 325
#> 325 328
#> 322 330
#> 317 333
#> 313 336
#> 306 337
#> 300 338
#> 292 339
#> 285 340
#> 277 339
#> 272 338
#> 265 336
#> 262 333
#> 259 330
floor(nrow(digito)/9)
#> [1] 8
par(mfrow=c(3,3))
for(i in 1:9){
plot(digito[1:(8*(i-1)+2),])
}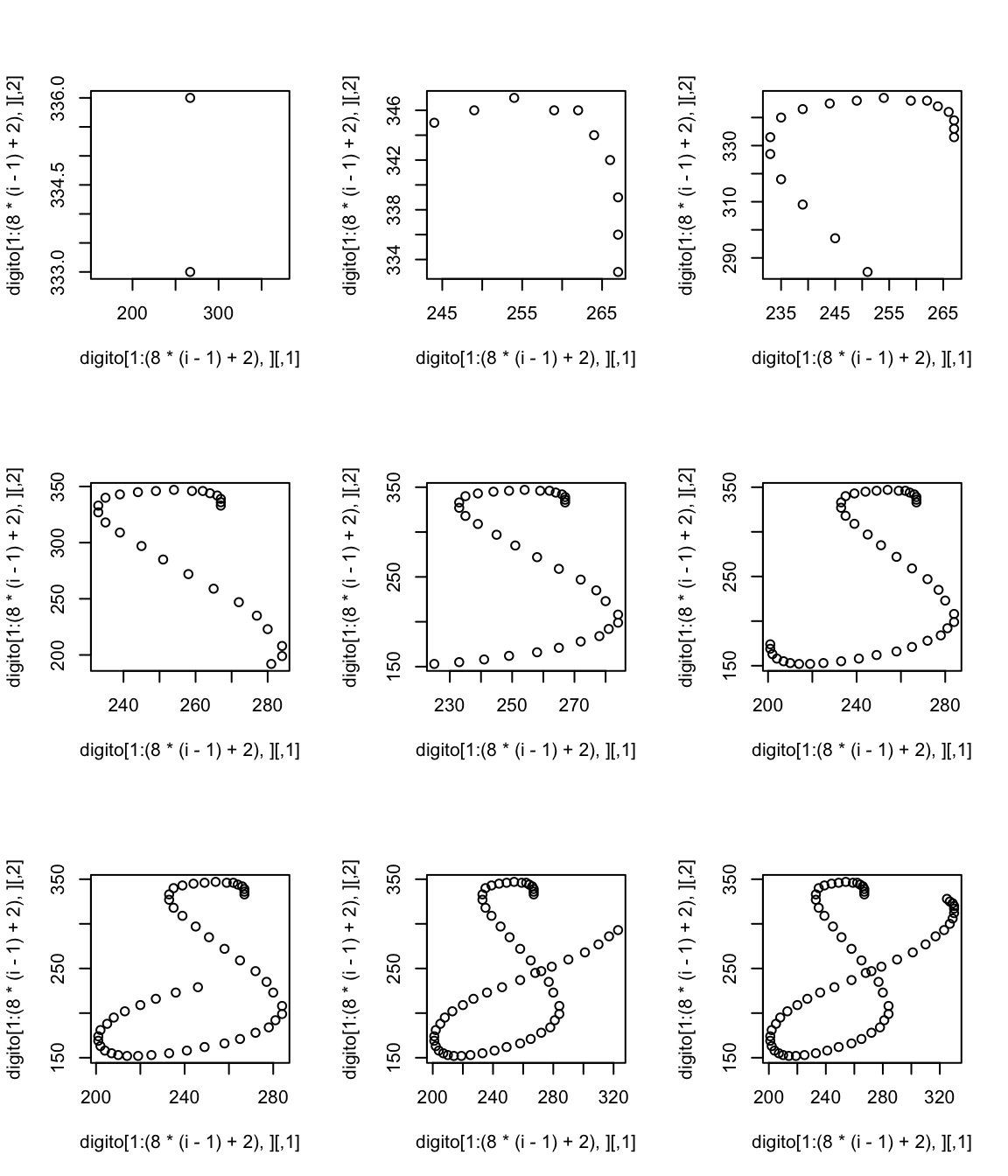
Nos interesa construir un modelo que describa la escritura de estos dígitos. Proponemos un modelo como sigue:
El espacio de estados ocultos tiene 16 estados distintos.
La matriz de transición entre estados es de izquierda a derecha. Es decir, la serie comienza en el estado 1, y solamente transiciona de 1 a 2, de 2 a 3 y así sucesivamente. Puede permanecer un número arbitrario de tiempos en cada estado.
Las observaciones son bivariadas: tenemos un ángulo de trazo (8 posibles direcciones), y una velocidad de trazo (que supondremos gaussiano). Supondremos estas dos variables son condicionalmente independientes dado el estado.
La idea general es:
Transformar los patrones de escritura a observaciones de ángulo y velocidad.
Ajustar un modelo distinto para cada uno de los dígitos.
Cuando observamos un dígito nuevo, calculamos la verosimilitud de la observación bajo los distintos modelos.
Clasificamos al dígito con verosimilitud más alta.
En estas notas veremos los primeros dos pasos.
La ventaja de usar HMM en este contexto es, en primer lugar, que no es necesario normalizar los dígitos a una longitud fija (aunque esto puede ayudar en la predicción), y mejor aún, que el modelo es flexible en cuanto a escalamientos de distintas partes de la escritura de los dígitos, por ejemplo, dibujar más lentamente unas partes, hacer un ocho con la parte de arriba más grande que la de abajo, etc.
Primero construimos funciones auxiliares:
# convertirSerie: recibe las coordenadas y devuelve el ángulo y la velocidad
convertirSerie <- function(patron){
d_1 <- rbind(patron[-1, ], c(NA,NA)) - patron
d_2 <- d_1[-nrow(d_1), ]
angulo <- acos(d_2[, 1] / (apply(d_2, 1, function(x) sqrt(sum(x ^ 2))))) *
sign(d_2[, 2])
velocidad <- apply(d_2, 1, function(x) sqrt(sum(x ^ 2)))
dat_out<- data.frame(angulo = angulo[], velocidad = velocidad[])
dat_out[!is.na(dat_out$angulo), ]
}
# trazar: recibe ángulo y velocidad y devuelve coordenadas
trazar <- function(datos){
angulos <- datos[, 1]
velocidad <- datos[, 2]
longitud <- length(angulos) + 1
puntos <- data.frame(x = rep(NA, longitud), y = rep(NA, longitud))
puntos[1, ] <- c(0, 0)
for(i in 2:length(angulos)){
puntos[i,] <- puntos[i - 1, ] + velocidad[i - 1] *
c(cos(angulos[i - 1]), sin(angulos[i - 1]))
}
puntos
}
con_ang <- convertirSerie(results.list[[6]])
con_ang
#> angulo velocidad
#> 1 0.69473828 7.810250
#> 2 0.67474094 6.403124
#> 3 1.57079633 4.000000
#> 4 0.00000000 2.000000
#> 5 -2.52134317 8.602325
#> 6 -2.46685171 12.806248
#> 7 -2.35619449 16.970563
#> 8 -2.25972072 22.022716
#> 9 -2.19628137 22.203603
#> 10 -2.18545928 20.808652
#> 11 -2.01317055 21.023796
#> 12 -1.92956700 17.088007
#> 13 -1.64210379 14.035669
#> 14 -1.30454428 11.401754
#> 15 -0.55859932 9.433981
#> 16 -0.09065989 11.045361
#> 17 0.00000000 11.000000
#> 18 0.17985350 11.180340
#> 19 0.46364761 8.944272
#> 20 0.78539816 8.485281
#> 21 1.37340077 5.099020
#> 22 2.24553727 6.403124
#> 23 2.62244654 8.062258
#> 24 2.92292371 9.219544
#> 25 3.05093277 11.045361
#> 26 -2.86329299 7.280110
#> 27 -2.97644398 6.082763
plot(trazar(con_ang))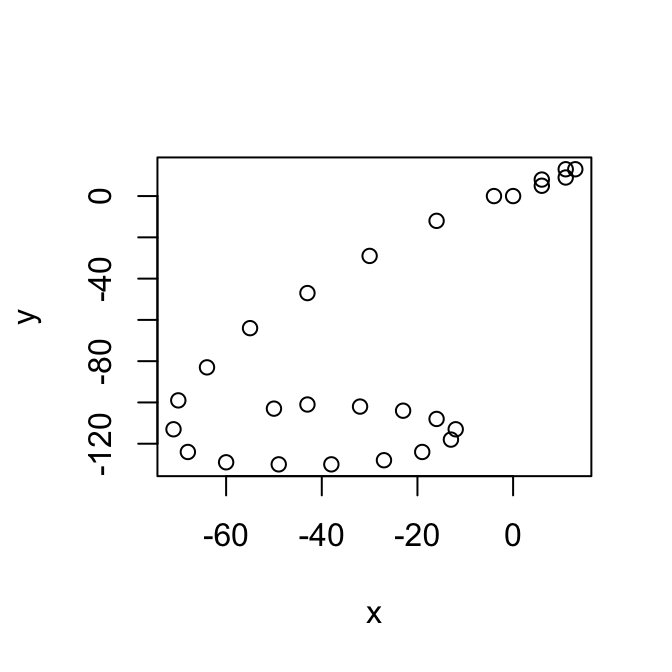
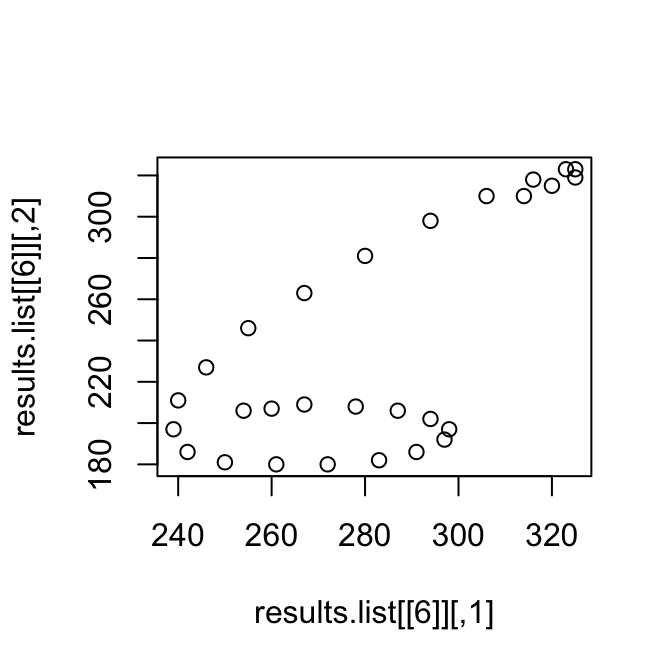
Comenzamos seleccionando los dígitos 8, convertimos los datos a una tabla, y categorizamos los ángulos:
library(Hmisc)
filtro <- sapply(digitos, function(x) x==8)
resultados <- results.list[filtro]
dat_8 <- ldply(1:700, function(i){
conv_1 <- convertirSerie(resultados[[i]])
data.frame(angulo = conv_1[,1], velocidad = conv_1[,2], serie=i,
tiempo=1:nrow(conv_1))
})
head(dat_8)
#> angulo velocidad serie tiempo
#> 1 1.570796 3.000000 1 1
#> 2 1.570796 3.000000 1 2
#> 3 1.892547 3.162278 1 3
#> 4 2.356194 2.828427 1 4
#> 5 2.356194 2.828427 1 5
#> 6 0.000000 3.000000 1 6
# Longitud de los dígitos
longitudes <- ddply(dat_8, 'serie', summarise, long=max(tiempo))
# Creamos 8 categorías usando cuantiles
dat_8$angulo_cat <- factor(cut2(dat_8$angulo, g = 8, levels.mean = TRUE))
levs <- as.numeric(levels(dat_8$angulo_cat))Ahora construimos nuestro modelo. Una diferencia importante en relación a los ejempos anteriores es que aquí tenemos varias series de tiempo observadas (cuyas longitudes están en el argumento ntimes abajo):
mod <- depmix(list(angulo_cat ~ 1, velocidad ~ 1), data = dat_8,
nstates = 16,
family = list(multinomial("identity"), gaussian()),
ntimes = longitudes$long)El modelo está incializado de la siguiente forma
summary(mod)
#> Initial state probabilties model
#> pr1 pr2 pr3 pr4 pr5 pr6 pr7 pr8 pr9 pr10 pr11 pr12
#> 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> pr13 pr14 pr15 pr16
#> 0.062 0.062 0.062 0.062
#>
#> Transition matrix
#> toS1 toS2 toS3 toS4 toS5 toS6 toS7 toS8 toS9 toS10 toS11
#> fromS1 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS2 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS3 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS4 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS5 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS6 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS7 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS8 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS9 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS10 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS11 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS12 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS13 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS14 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS15 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> fromS16 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062 0.062
#> toS12 toS13 toS14 toS15 toS16
#> fromS1 0.062 0.062 0.062 0.062 0.062
#> fromS2 0.062 0.062 0.062 0.062 0.062
#> fromS3 0.062 0.062 0.062 0.062 0.062
#> fromS4 0.062 0.062 0.062 0.062 0.062
#> fromS5 0.062 0.062 0.062 0.062 0.062
#> fromS6 0.062 0.062 0.062 0.062 0.062
#> fromS7 0.062 0.062 0.062 0.062 0.062
#> fromS8 0.062 0.062 0.062 0.062 0.062
#> fromS9 0.062 0.062 0.062 0.062 0.062
#> fromS10 0.062 0.062 0.062 0.062 0.062
#> fromS11 0.062 0.062 0.062 0.062 0.062
#> fromS12 0.062 0.062 0.062 0.062 0.062
#> fromS13 0.062 0.062 0.062 0.062 0.062
#> fromS14 0.062 0.062 0.062 0.062 0.062
#> fromS15 0.062 0.062 0.062 0.062 0.062
#> fromS16 0.062 0.062 0.062 0.062 0.062
#>
#> Response parameters
#> Resp 1 : multinomial
#> Resp 2 : gaussian
#> Re1.-2.77980 Re1.-1.98315 Re1.-1.23316 Re1.-0.48430 Re1. 0.76461
#> St1 0.125 0.125 0.125 0.125 0.125
#> St2 0.125 0.125 0.125 0.125 0.125
#> St3 0.125 0.125 0.125 0.125 0.125
#> St4 0.125 0.125 0.125 0.125 0.125
#> St5 0.125 0.125 0.125 0.125 0.125
#> St6 0.125 0.125 0.125 0.125 0.125
#> St7 0.125 0.125 0.125 0.125 0.125
#> St8 0.125 0.125 0.125 0.125 0.125
#> St9 0.125 0.125 0.125 0.125 0.125
#> St10 0.125 0.125 0.125 0.125 0.125
#> St11 0.125 0.125 0.125 0.125 0.125
#> St12 0.125 0.125 0.125 0.125 0.125
#> St13 0.125 0.125 0.125 0.125 0.125
#> St14 0.125 0.125 0.125 0.125 0.125
#> St15 0.125 0.125 0.125 0.125 0.125
#> St16 0.125 0.125 0.125 0.125 0.125
#> Re1. 1.27708 Re1. 2.03527 Re1. 2.76861 Re2.(Intercept) Re2.sd
#> St1 0.125 0.125 0.125 0 1
#> St2 0.125 0.125 0.125 0 1
#> St3 0.125 0.125 0.125 0 1
#> St4 0.125 0.125 0.125 0 1
#> St5 0.125 0.125 0.125 0 1
#> St6 0.125 0.125 0.125 0 1
#> St7 0.125 0.125 0.125 0 1
#> St8 0.125 0.125 0.125 0 1
#> St9 0.125 0.125 0.125 0 1
#> St10 0.125 0.125 0.125 0 1
#> St11 0.125 0.125 0.125 0 1
#> St12 0.125 0.125 0.125 0 1
#> St13 0.125 0.125 0.125 0 1
#> St14 0.125 0.125 0.125 0 1
#> St15 0.125 0.125 0.125 0 1
#> St16 0.125 0.125 0.125 0 1pero antes de ajustarlo, es necesario restringir los parámetros como describimos arriba (para tener un modelo de izquierda a derecha)
# usamos setpars para ver el orden de los parámetros y poder escribir las
# restricciones
setpars(mod, value=1:npar(mod))
#> Initial state probabilties model
#> pr1 pr2 pr3 pr4 pr5 pr6 pr7 pr8 pr9 pr10 pr11 pr12 pr13 pr14 pr15
#> 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
#> pr16
#> 16
#>
#> Transition matrix
#> toS1 toS2 toS3 toS4 toS5 toS6 toS7 toS8 toS9 toS10 toS11 toS12
#> fromS1 17 18 19 20 21 22 23 24 25 26 27 28
#> fromS2 33 34 35 36 37 38 39 40 41 42 43 44
#> fromS3 49 50 51 52 53 54 55 56 57 58 59 60
#> fromS4 65 66 67 68 69 70 71 72 73 74 75 76
#> fromS5 81 82 83 84 85 86 87 88 89 90 91 92
#> fromS6 97 98 99 100 101 102 103 104 105 106 107 108
#> fromS7 113 114 115 116 117 118 119 120 121 122 123 124
#> fromS8 129 130 131 132 133 134 135 136 137 138 139 140
#> fromS9 145 146 147 148 149 150 151 152 153 154 155 156
#> fromS10 161 162 163 164 165 166 167 168 169 170 171 172
#> fromS11 177 178 179 180 181 182 183 184 185 186 187 188
#> fromS12 193 194 195 196 197 198 199 200 201 202 203 204
#> fromS13 209 210 211 212 213 214 215 216 217 218 219 220
#> fromS14 225 226 227 228 229 230 231 232 233 234 235 236
#> fromS15 241 242 243 244 245 246 247 248 249 250 251 252
#> fromS16 257 258 259 260 261 262 263 264 265 266 267 268
#> toS13 toS14 toS15 toS16
#> fromS1 29 30 31 32
#> fromS2 45 46 47 48
#> fromS3 61 62 63 64
#> fromS4 77 78 79 80
#> fromS5 93 94 95 96
#> fromS6 109 110 111 112
#> fromS7 125 126 127 128
#> fromS8 141 142 143 144
#> fromS9 157 158 159 160
#> fromS10 173 174 175 176
#> fromS11 189 190 191 192
#> fromS12 205 206 207 208
#> fromS13 221 222 223 224
#> fromS14 237 238 239 240
#> fromS15 253 254 255 256
#> fromS16 269 270 271 272
#>
#> Response parameters
#> Resp 1 : multinomial
#> Resp 2 : gaussian
#> Re1.-2.77980 Re1.-1.98315 Re1.-1.23316 Re1.-0.48430 Re1. 0.76461
#> St1 273 274 275 276 277
#> St2 283 284 285 286 287
#> St3 293 294 295 296 297
#> St4 303 304 305 306 307
#> St5 313 314 315 316 317
#> St6 323 324 325 326 327
#> St7 333 334 335 336 337
#> St8 343 344 345 346 347
#> St9 353 354 355 356 357
#> St10 363 364 365 366 367
#> St11 373 374 375 376 377
#> St12 383 384 385 386 387
#> St13 393 394 395 396 397
#> St14 403 404 405 406 407
#> St15 413 414 415 416 417
#> St16 423 424 425 426 427
#> Re1. 1.27708 Re1. 2.03527 Re1. 2.76861 Re2.(Intercept) Re2.sd
#> St1 278 279 280 281 282
#> St2 288 289 290 291 292
#> St3 298 299 300 301 302
#> St4 308 309 310 311 312
#> St5 318 319 320 321 322
#> St6 328 329 330 331 332
#> St7 338 339 340 341 342
#> St8 348 349 350 351 352
#> St9 358 359 360 361 362
#> St10 368 369 370 371 372
#> St11 378 379 380 381 382
#> St12 388 389 390 391 392
#> St13 398 399 400 401 402
#> St14 408 409 410 411 412
#> St15 418 419 420 421 422
#> St16 428 429 430 431 432
pars <- c(unlist(getpars(mod)))
# Restringimos a solo poder ir del estado uno al dos, dos al tres, ...
# esto se hace modificando la inical de la matriz de transición
pars[17:272] <- 0
pars[sapply(1:16, function(i){0+17*i})] <- 1/2
pars[sapply(1:15, function(i){1+17*i})] <- 1/2
pars[255:256] <- 0.5
pars[272] <- 1
# restringimos estado inicial al 1
pars[2:16] <- 0
pars[1] <- 1
mod <- setpars(mod, pars)
summary(mod)
#> Initial state probabilties model
#> pr1 pr2 pr3 pr4 pr5 pr6 pr7 pr8 pr9 pr10 pr11 pr12 pr13 pr14 pr15
#> 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> pr16
#> 0
#>
#> Transition matrix
#> toS1 toS2 toS3 toS4 toS5 toS6 toS7 toS8 toS9 toS10 toS11 toS12
#> fromS1 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
#> fromS2 0.0 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
#> fromS3 0.0 0.0 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
#> fromS4 0.0 0.0 0.0 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0
#> fromS5 0.0 0.0 0.0 0.0 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0
#> fromS6 0.0 0.0 0.0 0.0 0.0 0.5 0.5 0.0 0.0 0.0 0.0 0.0
#> fromS7 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.5 0.0 0.0 0.0 0.0
#> fromS8 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.5 0.0 0.0 0.0
#> fromS9 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.5 0.0 0.0
#> fromS10 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.5 0.0
#> fromS11 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.5
#> fromS12 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5
#> fromS13 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
#> fromS14 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
#> fromS15 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
#> fromS16 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
#> toS13 toS14 toS15 toS16
#> fromS1 0.0 0.0 0.0 0.0
#> fromS2 0.0 0.0 0.0 0.0
#> fromS3 0.0 0.0 0.0 0.0
#> fromS4 0.0 0.0 0.0 0.0
#> fromS5 0.0 0.0 0.0 0.0
#> fromS6 0.0 0.0 0.0 0.0
#> fromS7 0.0 0.0 0.0 0.0
#> fromS8 0.0 0.0 0.0 0.0
#> fromS9 0.0 0.0 0.0 0.0
#> fromS10 0.0 0.0 0.0 0.0
#> fromS11 0.0 0.0 0.0 0.0
#> fromS12 0.5 0.0 0.0 0.0
#> fromS13 0.5 0.5 0.0 0.0
#> fromS14 0.0 0.5 0.5 0.0
#> fromS15 0.0 0.0 0.5 0.5
#> fromS16 0.0 0.0 0.0 1.0
#>
#> Response parameters
#> Resp 1 : multinomial
#> Resp 2 : gaussian
#> Re1.-2.77980 Re1.-1.98315 Re1.-1.23316 Re1.-0.48430 Re1. 0.76461
#> St1 0.125 0.125 0.125 0.125 0.125
#> St2 0.125 0.125 0.125 0.125 0.125
#> St3 0.125 0.125 0.125 0.125 0.125
#> St4 0.125 0.125 0.125 0.125 0.125
#> St5 0.125 0.125 0.125 0.125 0.125
#> St6 0.125 0.125 0.125 0.125 0.125
#> St7 0.125 0.125 0.125 0.125 0.125
#> St8 0.125 0.125 0.125 0.125 0.125
#> St9 0.125 0.125 0.125 0.125 0.125
#> St10 0.125 0.125 0.125 0.125 0.125
#> St11 0.125 0.125 0.125 0.125 0.125
#> St12 0.125 0.125 0.125 0.125 0.125
#> St13 0.125 0.125 0.125 0.125 0.125
#> St14 0.125 0.125 0.125 0.125 0.125
#> St15 0.125 0.125 0.125 0.125 0.125
#> St16 0.125 0.125 0.125 0.125 0.125
#> Re1. 1.27708 Re1. 2.03527 Re1. 2.76861 Re2.(Intercept) Re2.sd
#> St1 0.125 0.125 0.125 0 1
#> St2 0.125 0.125 0.125 0 1
#> St3 0.125 0.125 0.125 0 1
#> St4 0.125 0.125 0.125 0 1
#> St5 0.125 0.125 0.125 0 1
#> St6 0.125 0.125 0.125 0 1
#> St7 0.125 0.125 0.125 0 1
#> St8 0.125 0.125 0.125 0 1
#> St9 0.125 0.125 0.125 0 1
#> St10 0.125 0.125 0.125 0 1
#> St11 0.125 0.125 0.125 0 1
#> St12 0.125 0.125 0.125 0 1
#> St13 0.125 0.125 0.125 0 1
#> St14 0.125 0.125 0.125 0 1
#> St15 0.125 0.125 0.125 0 1
#> St16 0.125 0.125 0.125 0 1Ahora ajustamos usando EM:
set.seed(280572)
fm <- fit(mod, emcontrol=em.control(maxit=100))
#> converged at iteration 82 with logLik: -123820.9
summary(fm)
#> Initial state probabilties model
#> pr1 pr2 pr3 pr4 pr5 pr6 pr7 pr8 pr9 pr10 pr11 pr12 pr13 pr14 pr15
#> 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> pr16
#> 0
#>
#> Transition matrix
#> toS1 toS2 toS3 toS4 toS5 toS6 toS7 toS8 toS9 toS10 toS11
#> fromS1 0.777 0.223 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
#> fromS2 0.000 0.549 0.451 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
#> fromS3 0.000 0.000 0.636 0.364 0.000 0.000 0.000 0.000 0.000 0.000 0.000
#> fromS4 0.000 0.000 0.000 0.566 0.434 0.000 0.000 0.000 0.000 0.000 0.000
#> fromS5 0.000 0.000 0.000 0.000 0.463 0.537 0.000 0.000 0.000 0.000 0.000
#> fromS6 0.000 0.000 0.000 0.000 0.000 0.678 0.322 0.000 0.000 0.000 0.000
#> fromS7 0.000 0.000 0.000 0.000 0.000 0.000 0.631 0.369 0.000 0.000 0.000
#> fromS8 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.414 0.586 0.000 0.000
#> fromS9 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.547 0.453 0.000
#> fromS10 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.579 0.421
#> fromS11 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.582
#> fromS12 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
#> fromS13 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
#> fromS14 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
#> fromS15 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
#> fromS16 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
#> toS12 toS13 toS14 toS15 toS16
#> fromS1 0.000 0.000 0.000 0.000 0.000
#> fromS2 0.000 0.000 0.000 0.000 0.000
#> fromS3 0.000 0.000 0.000 0.000 0.000
#> fromS4 0.000 0.000 0.000 0.000 0.000
#> fromS5 0.000 0.000 0.000 0.000 0.000
#> fromS6 0.000 0.000 0.000 0.000 0.000
#> fromS7 0.000 0.000 0.000 0.000 0.000
#> fromS8 0.000 0.000 0.000 0.000 0.000
#> fromS9 0.000 0.000 0.000 0.000 0.000
#> fromS10 0.000 0.000 0.000 0.000 0.000
#> fromS11 0.418 0.000 0.000 0.000 0.000
#> fromS12 0.578 0.422 0.000 0.000 0.000
#> fromS13 0.000 0.683 0.317 0.000 0.000
#> fromS14 0.000 0.000 0.839 0.161 0.000
#> fromS15 0.000 0.000 0.000 0.696 0.304
#> fromS16 0.000 0.000 0.000 0.000 1.000
#>
#> Response parameters
#> Resp 1 : multinomial
#> Resp 2 : gaussian
#> Re1.-2.77980 Re1.-1.98315 Re1.-1.23316 Re1.-0.48430 Re1. 0.76461
#> St1 0.009 0.020 0.008 0.065 0.185
#> St2 0.054 0.032 0.014 0.310 0.030
#> St3 0.632 0.055 0.027 0.094 0.054
#> St4 0.002 0.878 0.072 0.047 0.000
#> St5 0.001 0.080 0.851 0.068 0.000
#> St6 0.000 0.035 0.202 0.763 0.000
#> St7 0.080 0.191 0.331 0.159 0.110
#> St8 0.000 0.225 0.748 0.028 0.000
#> St9 0.005 0.941 0.026 0.029 0.000
#> St10 0.833 0.005 0.006 0.151 0.000
#> St11 0.000 0.000 0.000 0.133 0.011
#> St12 0.000 0.000 0.000 0.007 0.067
#> St13 0.000 0.000 0.000 0.000 0.050
#> St14 0.000 0.000 0.000 0.000 0.880
#> St15 0.000 0.000 0.000 0.025 0.036
#> St16 0.384 0.152 0.007 0.097 0.000
#> Re1. 1.27708 Re1. 2.03527 Re1. 2.76861 Re2.(Intercept) Re2.sd
#> St1 0.324 0.306 0.083 5.718 2.998
#> St2 0.003 0.008 0.547 7.333 3.192
#> St3 0.065 0.026 0.047 10.939 4.907
#> St4 0.000 0.000 0.001 10.086 3.919
#> St5 0.000 0.000 0.000 12.803 4.393
#> St6 0.000 0.000 0.000 16.605 4.689
#> St7 0.053 0.034 0.041 18.121 8.923
#> St8 0.000 0.000 0.000 12.176 2.925
#> St9 0.000 0.000 0.000 9.563 2.715
#> St10 0.000 0.000 0.004 10.311 3.523
#> St11 0.000 0.003 0.854 10.423 3.505
#> St12 0.036 0.867 0.023 10.649 4.111
#> St13 0.950 0.000 0.000 14.767 5.537
#> St14 0.120 0.000 0.000 15.388 5.420
#> St15 0.475 0.464 0.000 7.886 2.856
#> St16 0.000 0.005 0.355 10.369 4.225Y podemos simular algunas trayectorias:
set.seed(2805)
fm_1 <- fm
class(fm_1) <- 'depmix'
sim_1 <- simulate(fm_1)
resp_1 <- sim_1@response
estados <- sim_1@states
angulosSim <- lapply(resp_1[estados], function(x){
params <- x[[1]]@parameters$coefficients
c(sample(levs, 1, prob=params ), rnorm(1, x[[2]]@parameters[1][[1]], sd=x[[2]]@parameters[2]$sd))
# rnorm(1, params[[1]], sd=params$sd )}
}
)
dat_x <- data.frame(Reduce(rbind, angulosSim))
names(dat_x) <- c('angulo','velocidad')
# estados
head(dat_x, 6)
#> angulo velocidad
#> init -0.48430 3.710607
#> X 2.76861 7.495466
#> X.1 -0.48430 9.371682
#> X.2 -0.48430 12.416008
#> X.3 2.76861 4.431659
#> X.4 -2.77980 9.127368
plot(trazar(dat_x[1:78,]), type='l')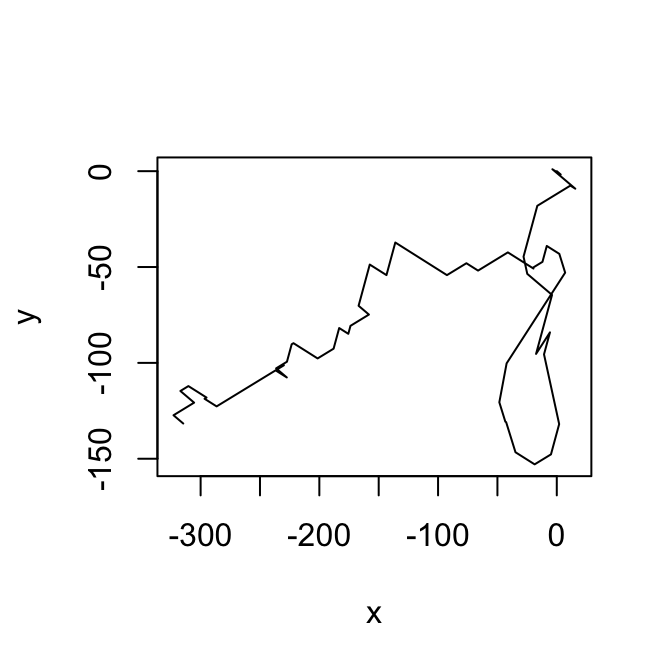
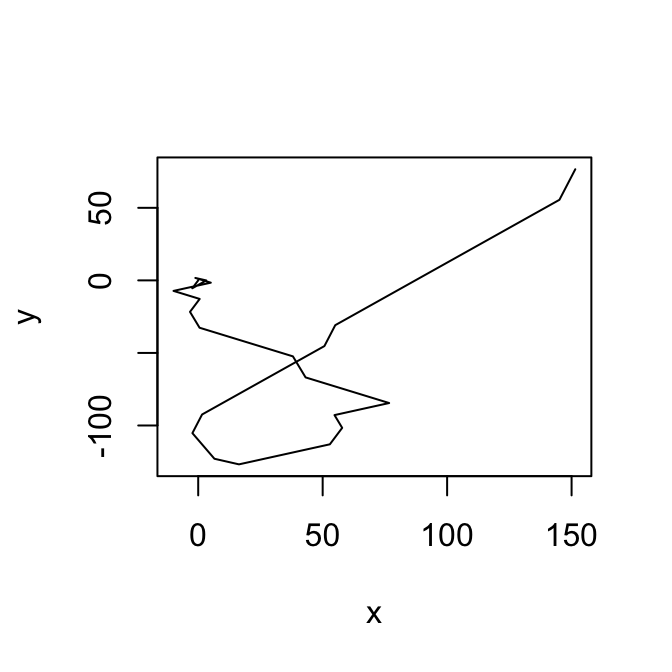
La ruta de máxima probabilidad (estados) se puede ver en el objeto posterior. Esta secuencia indica los estados más probables en el sentido de máxima probabilidad posterior (MAP).
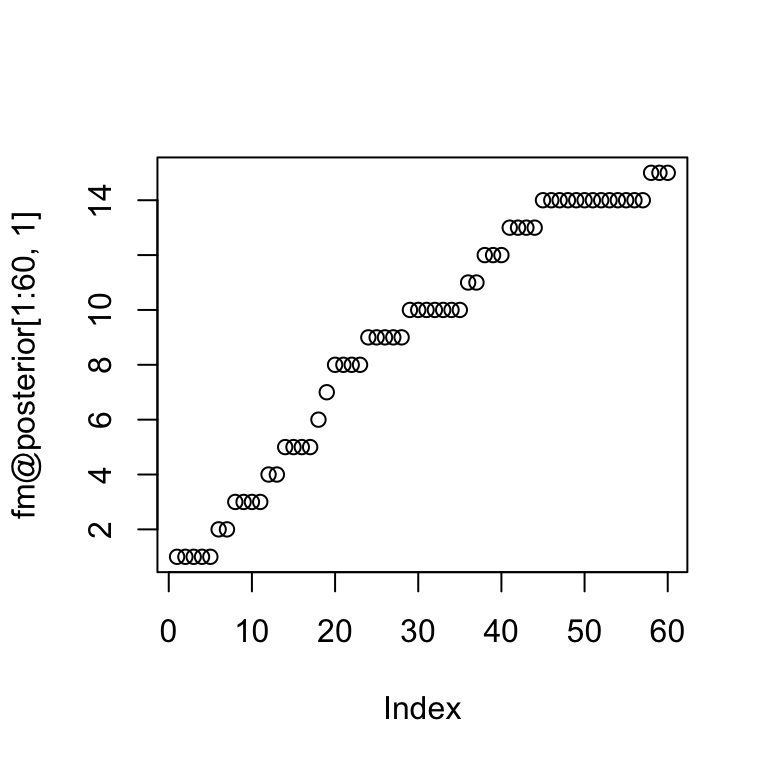
respuesta <- fm@response[fm@posterior[1:60,1]]
post <- ldply(respuesta, function(comp){
angulo.probs <- comp[[1]]@parameters$coefficients
velocidad <- comp[[2]]@parameters$coefficients
c(levs[which.max(angulo.probs)], velocidad)
})
names(post) <- c('angulo.cut','velocidad')
plot(trazar(post))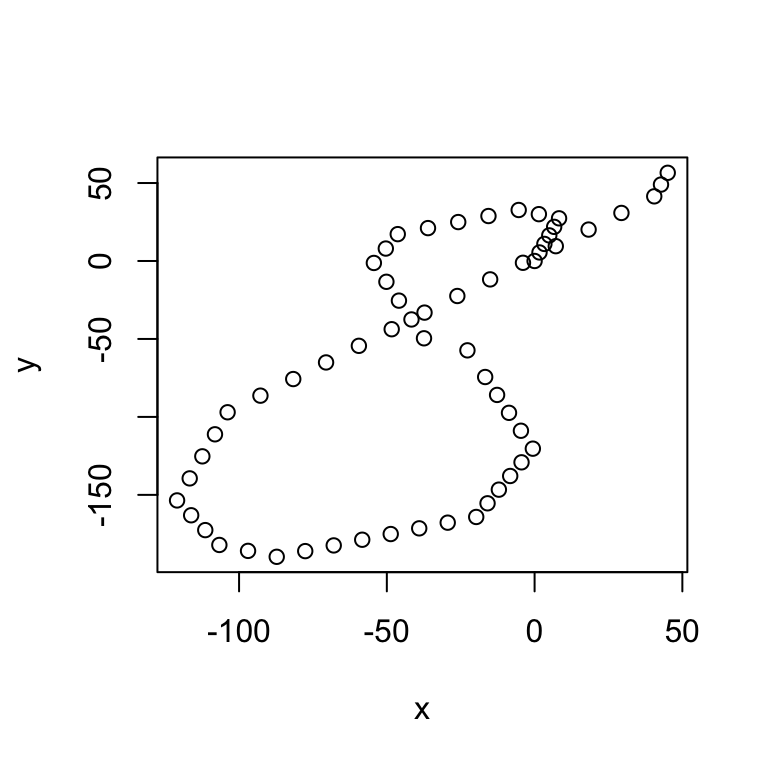
En el caso de arriba, se inició en el estado 1 (por construcción), permaneció ahí por 5 tiempos, pasó al estado 2,…
Veamos el caso del dígito 3:
load('data/pendigits/modelo_digitos_3.RData')
filtro <- sapply(digitos, function(x) x==3)
resultados <- results.list[filtro]
dat.6 <- ldply(1:500, function(i){
conv.1 <- convertirSerie(resultados[[i]])
data.frame(angulo=conv.1[,1], velocidad=conv.1[,2], serie=i, tiempo=1:nrow(conv.1))
})
longitudes <- ddply(dat.6, 'serie', summarise, long=max(tiempo))
dat.6$angulo.cut <- factor(cut2(dat.6$angulo, g=8, levels.mean=TRUE))
levs <- as.numeric(levels(dat.6$angulo.cut))
plot(fm@posterior[1:44,1])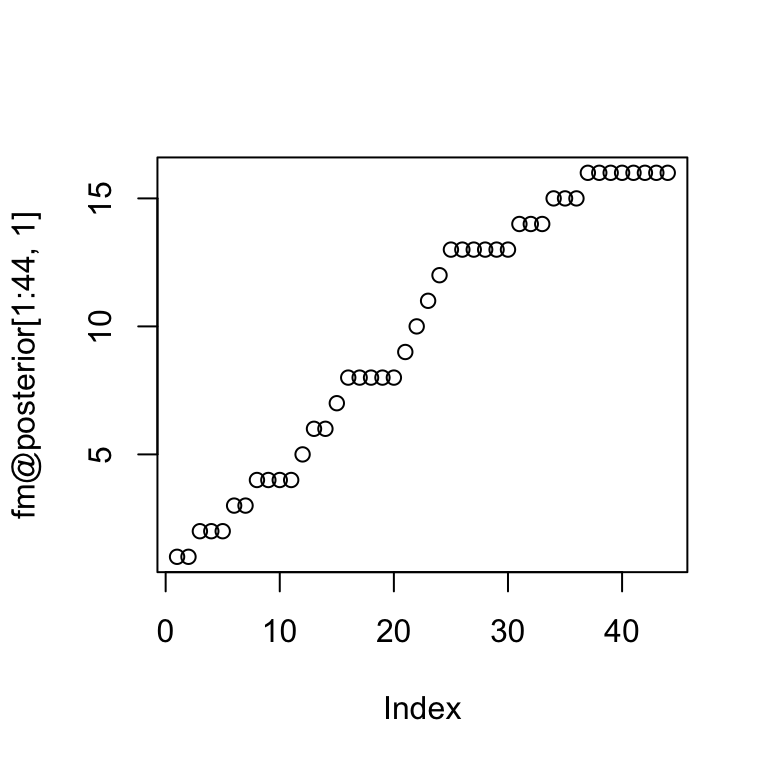
respuesta <- fm@response[fm@posterior[1:44,1]]
post <- ldply(respuesta, function(comp){
angulo.probs <- comp[[1]]@parameters$coefficients
velocidad <- comp[[2]]@parameters$coefficients
c(levs[which.max(angulo.probs)], velocidad)
})
names(post) <- c('angulo.cut','velocidad')
plot(trazar(post))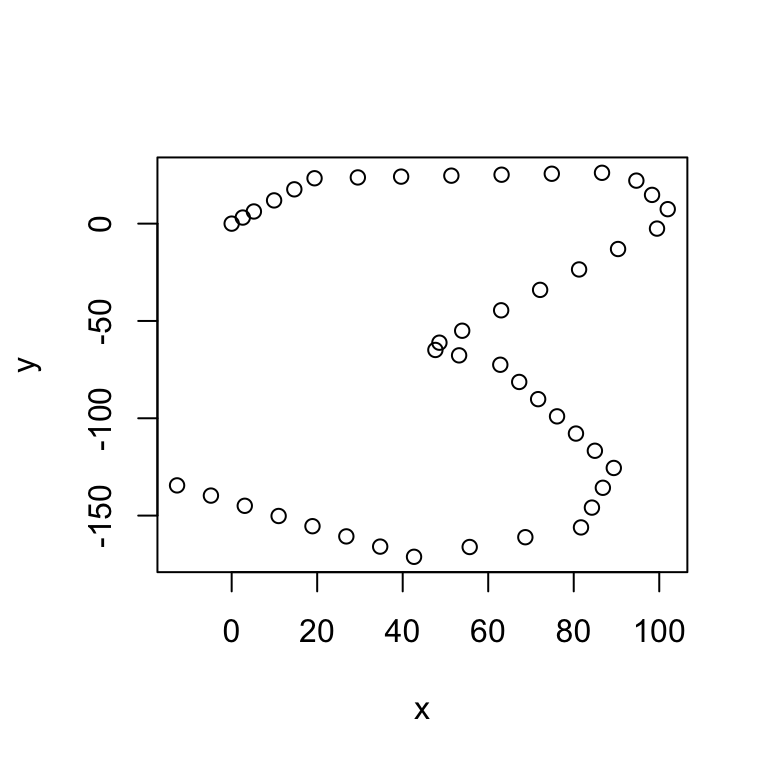
 * En HMM, la variable xn+1 es independiente de:
* En HMM, la variable xn+1 es independiente de:
x1,...,xn
x1,...,xn−1
xn−1
Ninguna de las anteriores.
- Sea A la matriz de transición en un HMM. Un modelo de mezclas para datos iid corresponde a un caso especial de HMM donde:
Ajk toman el mismo valor para toda j.
Ajk toman el mismo valor para toda j y para toda k.
Ajk toman el mismo valor para toda k.
- Ninguna de las anteriores.
7.2.1 Algoritmo EM para modelos markovianos de estados ocultos
Ahora veremos cómo se construye el paso E y M del algoritmo esperanza- maximización para HMM.
Similar al caso de varaibles latentes, comenzamos escribiendo la verosimilitud con datos completos. La serie de datos observados la denotamos como X=X1,…,XT y la de datos latentes S=S1,…,ST.
Supongamos que tenemos una observación x=x1,…,xT con s=s1,…,sT. Si suponemos que P(S1=s1)=1 la verosimilitud (usando nuestro modelo HMM) es
P(x,S=s)=P(x1|S1=s1)P(S2=s2|S1=s1)P(x2|S2=s2)⋯P(ST=sT|ST−1=st−1)P(xT|ST=sT).
Si denotamos pij=P(St=j|St−1=i) y pj=P(xt|St=j). Tomando logaritmo y reacomodando:
logP(x,S=s)=t∑t=2logpst−1,st+T∑t=1logpst(xt).
Nos conviene reescribir esta ecuación de otra manera. Introducimos entonces las variables indicadoras uj(t), tales que uj(t)=1 si y sólo si st=j, y vij(t), tales que vij(t)=1 si y sólo si st−1=i,st=j. Entonces podemos reescribr
logP(x,S=s)=M∑i=1M∑j=1(T∑t=2vij(t))logpij+M∑i=1T∑t=1ui(t)logpi(xt).
A partir de esta ecuación es fácil ver la forma del algoritmo.
- Paso E: Necesitamos calcular el valor esperado condicional (dados los datos observados X) de la expresión de arriba. Basta entonces calcular δj(t)=E(uj(t)|X)=P(St=j|X) y γij(t)=E(vij(t)|X)=P(St−1=i,St=j|X).
Una vez que calculamos estas cantidades (usando el algoritmo hacia adelante-hacia atrás, o de Baum-Welch, como veremos más adelante), procedemos al paso M.
- Paso M: Buscamos maximizar
M∑i=1M∑j=1(T∑t=2ˆγij(t))logpij+M∑i=1T∑t=1ˆδi(t)logpi(xt)
Notemos que la optimización de los parámetros de pi se puede separar de la correspondiente a ˆpij. Más aun, la optimización de ˆpij se puede separar para cada i.
Es fácil ver que ˆpij=ˆγij∑lˆγil donde ˆγij=T∑t=2ˆγij(t), que son conteos ponderados por las probabilidades que resultan del paso E.
Para el segundo término, tenemos que usar la forma particular de las densidades condicionales pj(x). Si suponemos pi densidad Normal ^μi y ^Σi resultan: ^μi=∑Tt=1^δi(t)xt∑Tt=1^δi(t) ^Σi=∑Tt=1^δi(t)(xt−ˆμi)(xt−ˆμi)T∑Tt=1ˆδ(t) es el mismo caso que en mezcla de normales. Como ejercicio, calcula para el modelo Poisson.