Sección 8 Datos espaciales

La estadística espacial tiene aplicaciones en áreas como climatología, ecología, salud y bienes racíces, esto se debe a que en estas áreas es común contar con información espacial que deseamos modelar y es necesario incorporar el efecto de la autocorrelación espacial en la estimación y predicción.

La autocorrelación espacial se puede expresar informalmente como (primera ley de la geografía de Tobler):

Todo esta relacionado con todo, pero las cosas cercana
están más relacionadas que las lejanas.

Usualmente la estadística espacial se divide en tres ramas:

1. Análisis de datos de variación continua comprende procesos estocásticos cuyos valores pueden ser conocidos en todos los puntos del área de estudio.

El proceso $Y\left(s\right)$ es un vector aleatorio en una ubicación $s\in R^r$ donde $s$ varía de manera continua sobre el dominio $D\subset R^r$ (usualmente r= 2).

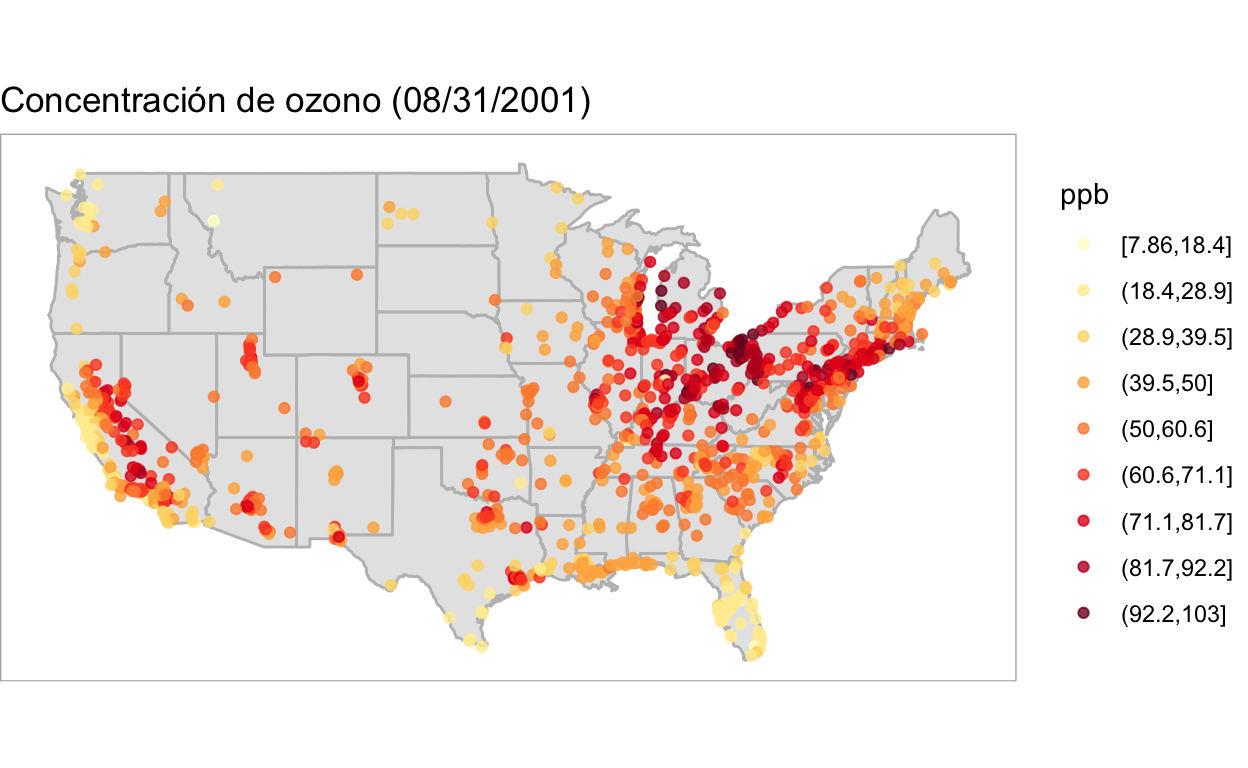
¿Qué preguntas interesantes puedes responder?

2. Análisis de datos de variación discreta (datos sobre áreas): Se refiere a la distribución de eventos cuya localización se asocia a zonas delimitadas por polígonos.

$D$ es nuevamente un subconjunto fijo de $R^r$, pero en este caso $D$ esta particionado en un número finito de unidades de area con fronteras bien definidas.

#> Regions defined for each Polygons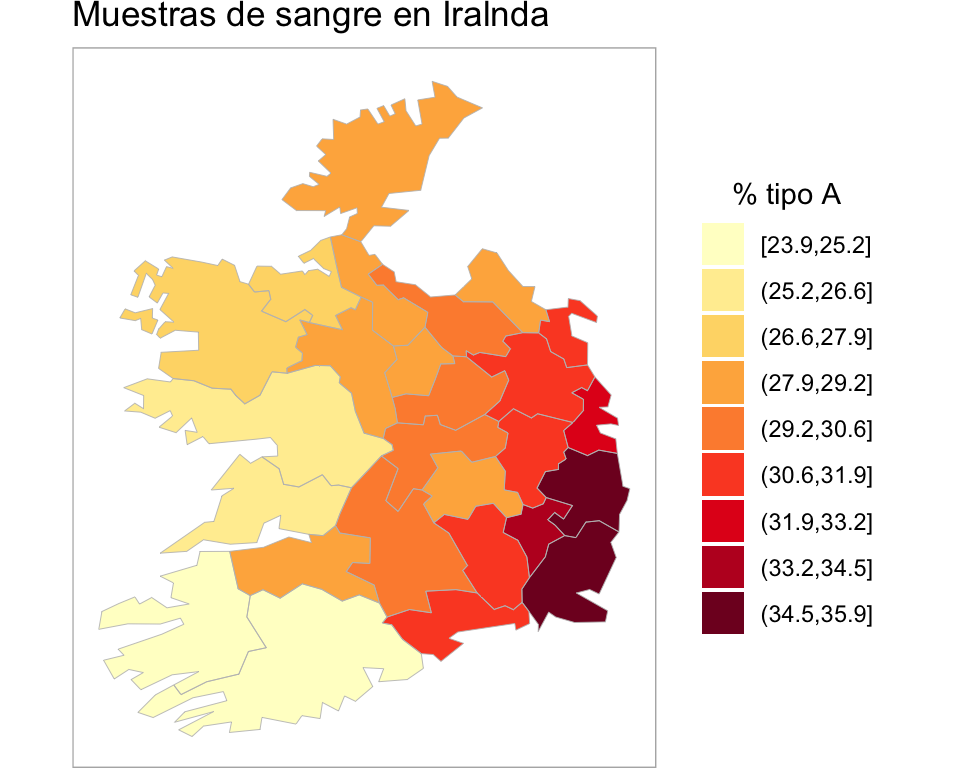

3. Análisis de procesos espaciales de puntos: Conjunto de puntos distribuidos en un área fija cuya ubicación fue generada por un mecanismo estocástico.

$D$ es aleatorio y sus índices indican la ubicación de eventos aleatorios que son el proceso puntual.

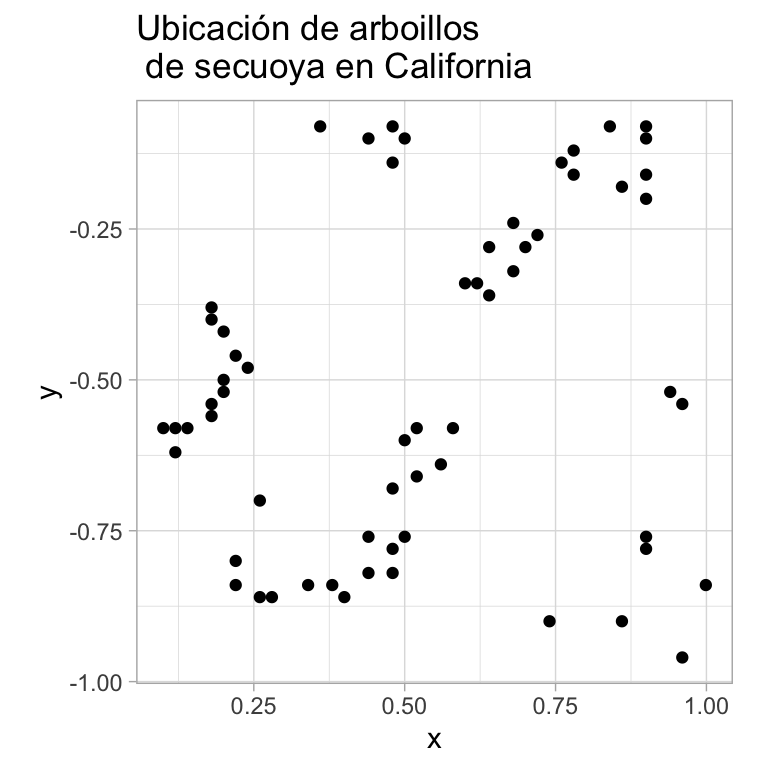
Supongamos $Z_1,...,Z_n$ variables aleatorias i.i.d. Gaussianas, con media $\mu$ y varianza conocida ${\sigma }_0^2$.

• Entonces: $$\hat{\mu }=\frac{1}{n}\sum _{i=1}^n{Z}_i$$ es un estimador insesgado para $\mu$ y $$Var\left(\hat{\mu }\right)=\frac{{\sigma }_0^2}{n}$$

• Supongamos ahora que $Z_1,...,Z_n$ son v.a. Gaussianas con media $\mu$ desconocida y varianza ${\sigma }_0^2$, supongamos además que las variables están correlacionadas positivamente: $$Cov(Z_i,Z_j)={\sigma }_0^2{\rho }^{|i-j|}$$ donde $0<\rho <1$.

1. Sea $\hat{\mu }=\frac{1}{n}{\sum }_{i=1}^n{Z}_i$. ¿$\hat{\mu }$ es un estimador insesgado para $\mu$?

1. Sí

2. No

3. No se puede saber

2. $Var\left(\hat{\mu }\right)$ es

1. Menor a $\frac{{\sigma }_0^2}{n}$.

2. Mayor a $\frac{{\sigma }_0^2}{n}$.

3. Igual a $\frac{{\sigma }_0^2}{n}$.

4. No se puede saber.